Original Video：【俗说矩阵】矩阵原来这么简单！从二元一次方程组开始教你~ - 晓之车高山老师 - bilibili

Linear equations system

Linear equation in 2 variables (二元一次方程): An equation has 2 unknown variables with an exponent of 1.

Two linear equations in 2 variables can make up a system of linear equations (线性方程组).

Gaussian elimination

Two kinds of Gaussian elimination to solve this linear system:

1. Reformalize the 1st equation and substitute it into the 2nd one, such that it comes down to a linear equation in 1 variable. (代入消元法)
   $\begin{cases}y=3-x\\\ 2x+3y=8 \end{cases}$ ➔ 2x+3(3-x)=8 ➔ $\\{^{x=1}\_{y=2}$

2. Multiply the equation with a certain number and add the 2 equations together to cancel a variable, such that only 1 linear equation is left. (加减消元法)
   $\begin{cases}-2x-2y=-6\\\ 2x+3y=8 \end{cases}$ ➔ y=2 ➔ $\\{^{x=1}\_{y=2}$

Geometric interpretation

A linear equation in 2 variables is a line on a plane. The solution of the linear system is the intersection of these lines.

Two kinds of linear system:

1. Homogeneous system: all of the constant terms are zeroes. $\begin{cases} x+y = 0\\\ 2x+3y = 0 \end{cases}$

2. Nonhomogeneous system: The constant term is not all zero. $\begin{cases} x+y = 3\\\ 2x+3y = 8 \end{cases}$

Solution of Homogeneous system has 2 cases

The lines are all passing through the origin.

1. If the slopes are different ($\\{^{x+y=0}\_{2x+3y=0}$ ➔ x=y=0), the only intersection of them is the origin. This means the homogenous system has only zero solution.

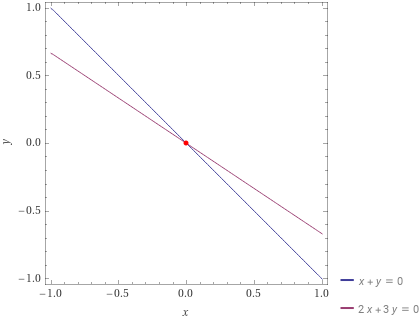
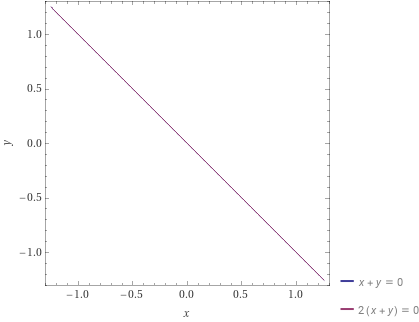
2. If the slopes of them are identical ($\\{^{x+y=0}\_{2x+2y=0}$ ➔ x=-y), the lines are overlapping. The solution set is a line: any point on the line is a solution of this system. That means there are infinitely many non-zero solutions besides the zero solution. There exists non-zero solution in this system.

Solution of Non-homogeneous system has 3 cases

1. Lines have distinct slopes ($\\{^{x+y=3}\_{2x+3y=8}$), so there is only one intersection corresponding to the single unique solution.

2. Lines are overlapping ($\\{^{x+y=3}\_{2x+2y=6}$). Any point on the line is a solution of this system. The system has infinitely many solutions.

3. Lines are parallel without any intersection ($\\{^{x+y=3}\_{2x+2y=4}$), this system has no solution. (Its solution must not be zero.)

Therefore, the assertion “The number of unknowns is the number of equations needed.” works only for the situation of “only zero solution” in a homogeneous system and “single unique solution” in a non-homogeneous system.

In the scenario with more variables, or the numbers of unknowns and equations are not equal, even if the gaussian elimination can be applied, the correct steps or the direction of elimination are hard to determine.

How to solve a linear system?

A general homogeneous system is a combination of m linear equations in n unknowns.

where

• x₁, x₂, …,xₙ are the n unkowns,

• The coefficient aₘₙ, the first subscript represents the ordinal number of the equation, and the second subscript stands for the unknown that this coefficient multiplies with.

  For example a₃₂ is the coefficient in the 3rd equation for the unknown x₃.

• Coefficients of each row cannot be all 0 and all of the parameters of an unknown cannot be all 0, so these m equations and n unknowns are effective.

Homogeneous Linear system with 3 variables

Each row is a inner product of two 3-dimensional vectors:

x₁ + 3x₂ + 5x₃ = 0 ➔ (1 3 5)(x₁ x₂ x₃) = 0
2x₁ + 4x₂ + 6x₃ = 0 ➔ (2 4 6)(x₁ x₂ x₃) = 0
2x₁ + 5x₂ + 8x₃ = 0 ➔ (2 5 8)(x₁ x₂ x₃) = 0

There are 2 types of vector:

1. Row vector (1 2 3)
2. Column vector $\[^1\_{^2\_3}\]$ or (1 2 3)ᵀ

Stack the above 3 expressions:
$\begin{bmatrix}1 & 3 & 5\\\ 2 & 4 & 6\\\ 2 & 5 & 8 \end{bmatrix} ⋅ (x₁\ x₂\ x₃) = \begin{bmatrix}0\\\ 0\\\ 0\end{bmatrix}$

The left array is matrix. This linear system can be regarded as a function:
$f( (x₁\ x₂\ x₃) ) = \begin{bmatrix} 0\\\ 0\\\ 0 \end{bmatrix}$

which maps 3 variables to 3 zeros, i.e., maps a unknown (row) vector to a zero (column) vector 𝟎.

To normalize the notations, the unknown vector is written as a column vector 𝒙, such that the linear system can be represented by matrix:

Therefore, the expression represents the mapping linearly from a column vector to another column vector.

$f(\begin{bmatrix} x₁\\\ x₂\\\ x₃ \end{bmatrix}) = \begin{bmatrix} 0\\\ 0\\\ 0 \end{bmatrix}$

Here, the matrix is arranging all the coefficients into an array based on their positions. Hence, it’s called coefficient matrix 𝑨.

Then this linear system can be expressed consiscely as: 𝑨𝒙=𝟎.

From the view of function, the function $f(\begin{bmatrix} x₁ \\\ x₂ \\\ x₃ \end{bmatrix})=\begin{bmatrix} 0\\\ 0\\\ 0 \end{bmatrix}$ can be written as f(𝒙)=𝟎.

The coefficient matrix 𝑨 plays the role of function f, that means the coefficient matrix maps the unknown vector to zero vector.

Non-homogeneous linear system

A non-homogeneous linear system contains m linear equations with n unknowns, where their constant termsare not all 0.

The notation is the same as homogeneous system and b₁, b₂,…, bₙ are not all 0.

For instance, the following non-homogeneous linear system can be represented as matrix:

Here, the coefficient matrix 𝑨 maps the column vector to a known non-zero column vector:

Elementary row operations are equivalent to Gaussian elimination.