Video 14 Overfitting 2021-11-17

Outline:

1. What is overfitting?
2. The role of noise
3. Deterministic noise
4. Dealing with overfitting

An Illustration of Overfitting on a Simple Example

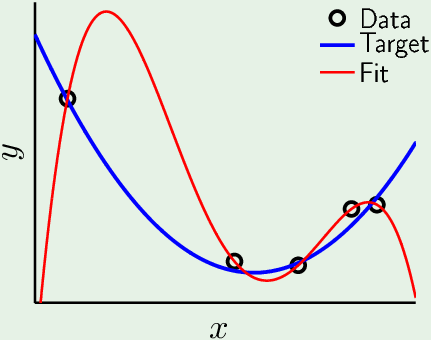
蓝色曲线是 unknowen target function。从这未知函数中生成5个样本点，因为有噪声，所以它们偏离了曲线。 根据这5个点去近似未知函数。因为噪声的存在，在用4阶的多项式（有5个参数）拟合这生成的5个点时，出现了过拟合：$E_{in}=0;\ E_{out} \gg 0$。（如果没有噪声，有可能使用相同阶数的模型就能完美拟合。为了拟合带噪声的数据，就使用了超过样本所表达信息的高阶模型，造成Eout 很大）

What is Overfitting?

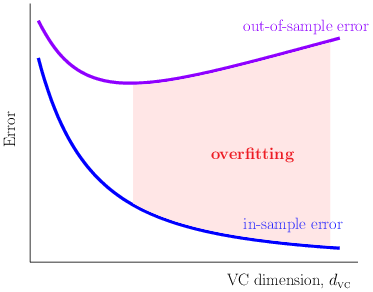
• 随着VC 维的增加，$E_{in}$ 不断下降，$E_{out}$反而上升。

  拟合数据的程度超过了样本数据应有(支持)的程度 (Fitting the data more than is warranted)

• 随着 VC 维的增加，假设集$\mathcal H$中的模型复杂度增加，对未知函数的近似能力增强，虽然generalization error在增加，但一开始，$E_{in}$ 和 $E_{out}$ 都在下降。超过某一点后，$E_{in}$继续减小，$E_{out}$反而上升，Generalization error 变更大:

  

• 实验两种情况：一个10阶的函数有噪声采样15个样本，一个50阶的函数无噪声采样15个样本：

  

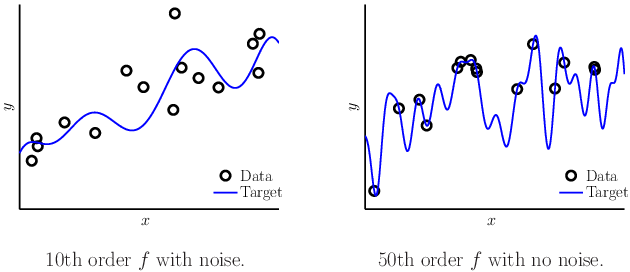
  分别用2阶和10阶的多项式去拟合：

  

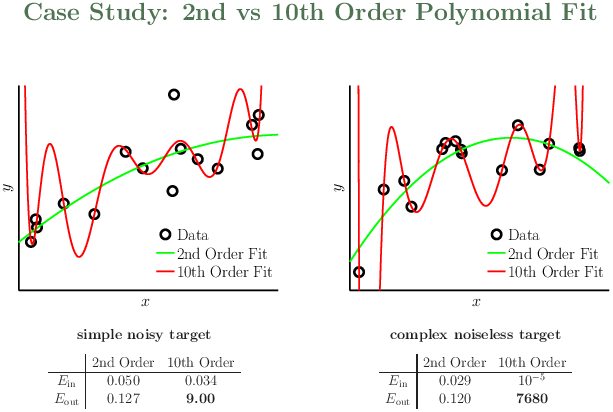
  从2阶模型转到10阶模型，穿过了更多的样本点，Ein更小了，但Eout变大了，说明出现了过拟合。简单模型甚至好于无噪声的复杂目标函数。noise 的阶数可能很高，所以简单模型的Ein 比较差。但是没有噪声的高阶目标函数样本也存在某种“噪声”：determinstic noise.

  假设集$\mathcal H$ should match to the quantity and quality of the data, than the complexity of unknown target function.

  两个学习器：O (overfitting) 和 R (restricted)

  …….

  结果:

  

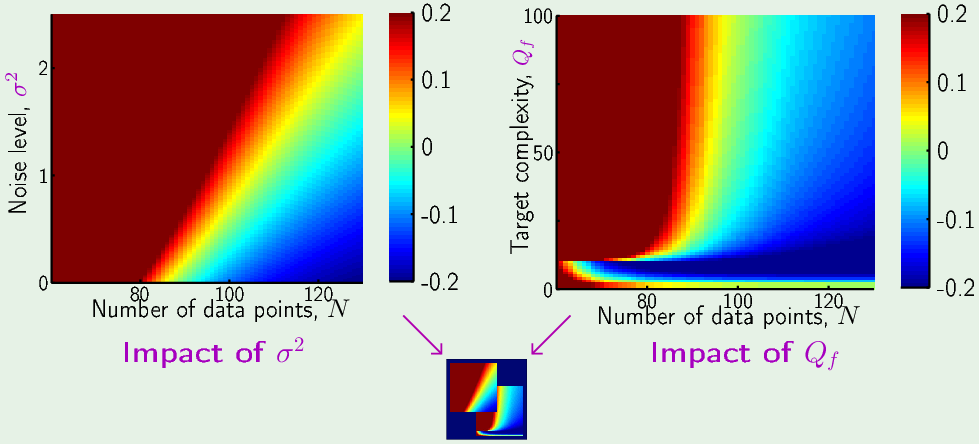
  左图，固定目比函数的复杂度为20th 阶多项式，随着增加噪声能量，样本的数量越来越不足以表达出目标函数的复杂度，这时希望不断减小Ein，非要拟合出超出数据表达范围的部分来减小Eout 会事与愿违，适得其反，南辕北辙，导致错误的形式，Eout反而越来越大，所以过拟合越来越严重。增加样本数量，可以减小过拟合。

  右图，无噪声的高阶目标函数样本，固定噪声能量 $\sigma^2=0.1$。随着增加目标函数的复杂度，过拟合也越来越严重。所以这里存在另一种不同于左图随机噪声的“确定性噪音”。

Deterministic noise

• 是假设集$\mathcal H$ 无法捕捉到的 f 的部分。(The part of f that H cannot capture)

  

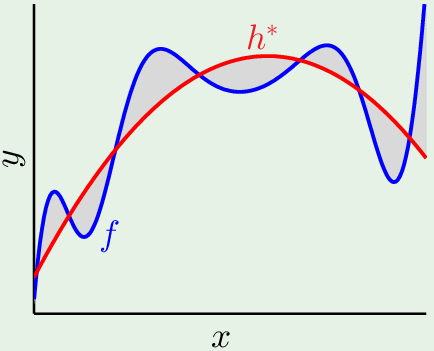
  因为模型复杂度有限，所以假设集中的最佳假设无法拟合目标函数的某些部分，$h^\star$ 与目标函数 f 之间的面积就是确定性噪音: $f(\mathbf x) - h^\star(\mathbf x)$。假设集太简单，无法表达出目标函数的复杂度，它无法理解的部分会给它带来困扰，当它尝试拟合这些能力范围之外的东西，就会导致错误的形式。那些无法理解的东西对它来说就是噪音。当使用更复杂的假设集，确定性噪声就会减小，因为它可以捕捉到更多

• 确定性噪声与随机噪声的主要区别:

  1. 确定性噪音取决于假设集$\mathcal H$，而随机噪声对所有的假设集都一样，Nothing can capture it, therefore it’s noise.
  2. 对于一个给定的样本$\mathbf x$，确定性噪声的量是固定的，就是 $f(\mathbf x) - h^\star(\mathbf x)$。而随机噪声，两个相同的x，产生的噪声大小是随机的。 但是它们两者对机器学习造成的影响是相同的，因为数据集是给定的（一次使用），假设集一旦确定它的确定性噪声也固定了。So in a given learning situation, they behave the same.

Impact on overfitting

1. 确定性噪声造成的过拟合在10阶以上的target complexity 才出现，因为这里的假设集是10阶的，超出10阶的部分它才无法近似。
2. 噪声造成过拟合是因为有限的样本，让你误以为你可以完美拟合。但其实随机噪声是捕捉不到的，而且当目标函数复杂度高于假设集的时候，确定性噪声也是捕捉（学）不到的。你以为你学到了，但其实造成了过拟合。

Noise and bias-variance

Eout 被分成了两部分，其中的 f 是没有噪声的，如果给样本数据加入噪声，上式会如何变化？

给定actual output：$y = f(\mathbf x) + \varepsilon(\mathbf x)$，假设噪声期望是0：$\mathbb E[\varepsilon(\mathbf x)] = 0$

$$ \begin{aligned} & \mathbb E_{\mathcal D,\varepsilon} \left[ \left( g^{(\mathcal D)}(\mathbf x) - y \right)^2 \right] & \text{$\varepsilon$影响了y，也要对ε求期望}\

&= \mathbb E_{\mathcal D,\varepsilon} \left[ \left( g^{(\mathcal D)}(\mathbf x) - f(\mathbf x) -\varepsilon(\mathbf x) \right)^2 \right] & \text{加一个减一个} \

&= \mathbb E_{\mathcal D,\varepsilon} \left[ \left( g^{(\mathcal D)}(\mathbf x) - \bar g(\mathbf x) +\bar g(\mathbf x) - f(\mathbf x) -\varepsilon(\mathbf x) \right)^2 \right] \

&= \mathbb E_{\mathcal D,\varepsilon} \left[ \left( g^{(\mathcal D)}(\mathbf x) - \bar g(\mathbf x) \right)^2

• \left( \bar g(\mathbf x) - f(\mathbf x) \right)^2
• \left( \varepsilon(\mathbf x) \right)^2 + \text{cross term} \right] \end{aligned} $$

求期望之后 cross term 都变成0了，因为它们包含ε，ε 的期望为0。前面两项只与数据集有关，而与训练样本的噪声ε无关，所以原来（没加噪声）等于0的项现在还等于0。Eout 只剩三项：

$$ E_{out} = \underbrace{ \mathbb E_{\mathcal D,\mathbf x} \left[ \left( g^{(\mathcal D)}(\mathbf x) - \bar g(\mathbf x) \right)^2 \right] }_{var}

• \underbrace{ \mathbb E_{\mathbf x} \left[ \left( \bar g(\mathbf x) - f(\mathbf x) \right)^2 \right] }_{\substack{bias \↑ \ \text{deterministic noise}}}
• \underbrace{ \mathbb E_{ε, \mathbf x} \left[ \left( \varepsilon(\mathbf x) \right)^2 \right] }_{\substack{\sigma^2 \ ↑ \ \text{stochastic noise}}} $$

第三项是 target 与 actual output之间的差距，就是随机噪声，第二项是"平均假设"（最佳假设the best thing you can do）与target 之间的差距，它无法拟合的部分就是确定性噪声。

两个噪声是平等的，因为增加样本数量，方差缩小，但两个噪声不可避免的（假设集给定，数据集给定，整体的近似就确定了）。当假设尝试拟合噪声时，就产生了方差（和过拟合）。

Two cures

Regularization: putting the brakes 踩刹车（增加一点限制; 提前停止）

Validation: Checking the bottom line 找到底线（找到比Ein 更好的反映拟合质量的误差$E_{CV}$）