Table of contents
Multi-Layer Perceptron
MLP consists of many layers of perceptrons. MLP 由多层感知机构成。 Perceptrons 只能解决线性二分类问题,是因为它采用的阶跃激活函数: $e(t)=\\{^{0,t<0}_{1,t>0}$,只能确定多维输入空间中的一个超平面_。
比如在二维空间中,它就无法解决异或问题。要产生非线性(斜率不固定)的决策边界可以换用非线性的激活函数,sigmoid function, tanh 或者 ReLu等等。它们使得感知机可以表达曲线,也就是即使输入超过阈值一些,输出没有对应的变化,依然为0。此时输入输出不再是线性关系,而不像阶跃函数,超过阈值就输出1。引入非线性之后,多层感知机才可以逼近任意非线性的决策边界。否则,MLP就相当于多条直线加权相加,最终得到的还是一条直线4,只能给出0-1分类。(这里的多条直线并不是联立求方程组,可以限定一块区域,而是被感知机加权,最后还是一条直线: wn(…(w2(w1+b1)+b2+…+bn) )。Example with cubic function.6
另一方面非线性激活函数可以帮助自动调整权重。多层感知机会带来大量需要调节的权重 w 1,手动调节是不可能实现的。阶跃函数的纵轴是0或1,横轴是wx(激活值),w的微小变化会导致激活值发生变化,如果输出层采用阶跃函数,output可能会跳变(在零点处不可微),就无法直接求导找到输出与输入之间的关系2。为了量化微小变化Δw带给输出的偏差,需要把台阶铺开,也就是变成sigmoid函数。从此目标就是调整 w 使MLP输出与目标值之间的误差e不断降低。而w的变化方向应该是使误差下降最快的方向,也就是梯度方向,就需要e对w求导数(e 先对 sigmoid 求导,sigmoid 再对 w求导),再乘以步长就是 w 每次需要修正的量。
同时,网络中其余的感知机也都要使用sigmoid函数,才能求得网络中所有w的导数。 因为误差e是前一层感知机输出Z的函数,比如采用最小二乘法,则 e = (σ(Z)-target)²,根据链式法则,需要对左侧一层的激活函数求导才能求得之前 w 的导数。如果它们仍采用阶跃激活函数,导数在非零处为零,但在零点处不可导3,就无法修正之前的w,也就无法完成误差的反向传播。
MSE 对 σ 求导:((σ(z)-target)²)’ = 2σ(z), σ 对 z 求导:σ(z)’ = σ(z)(1-σ(z)), z 对 w 求导:x(来自上一层的输出,或是网络Input), 所以输出层的 w 的导数为:2σ(z)∗σ(z)(1-σ(z))∗x(简化为 δ∗x)
要求左侧一层的 w₋₁ 的导数,根据 chain rule: 这层的z对 x (也就是 σ₋₁(z₋₁)) 的导数: w, x 对 z₋₁ 的导数:σ(z₋₁)(1-σ(z₋₁)), z₋₁ 对 w₋₁ 的导数:x₋₁, 所以e对左侧一层的 w₋₁ 的导数为:δ∗w∗σ(z₋₁)(1-σ(z₋₁))∗x₋₁(简化为 δ₋₁∗x₋₁)
再往左的话,即 δ₋₂∗x₋₂ , …
对于输出层有多个神经元,误差是多个神经元输出之和,所以e求导的时候要兵分多路,e分别对每一路求导数,然后加起来。4
(2022-12-25) 比如下图中,有两个输出神经元 y₁^, y₂^,求 e 对 w₁ 的梯度∂e/∂w₁,就是两个输出神经元分别对 w₁ 求梯度,再加起来。
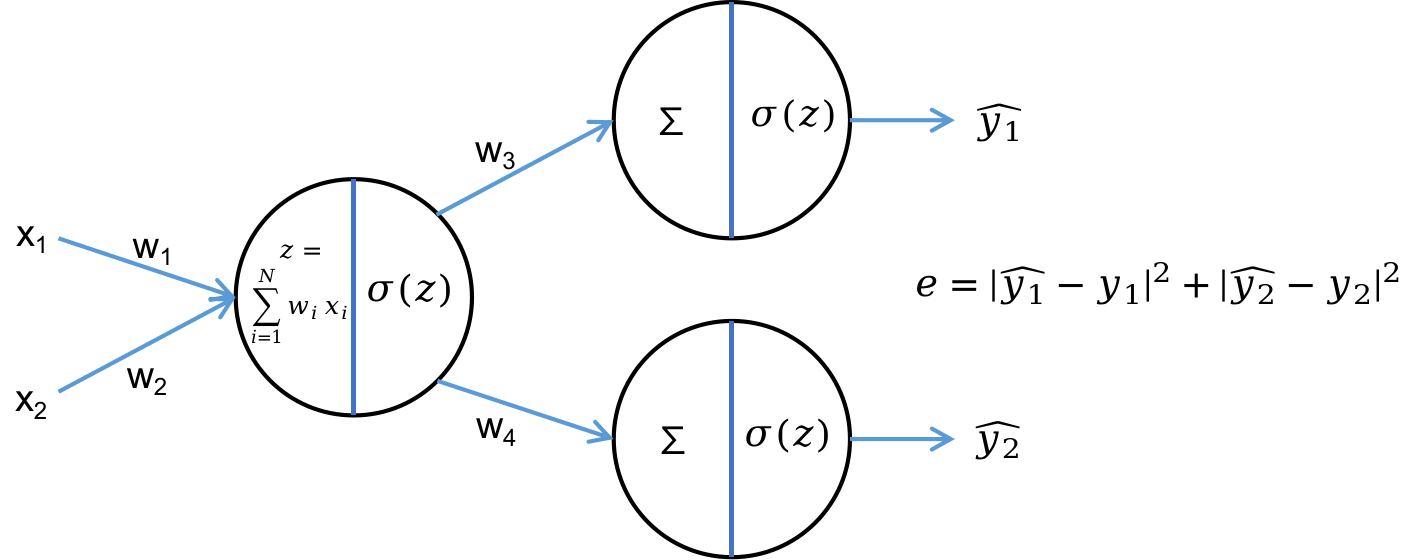
刘二那个反向传播的图,分两路:一路对x求导,一路对w求导。
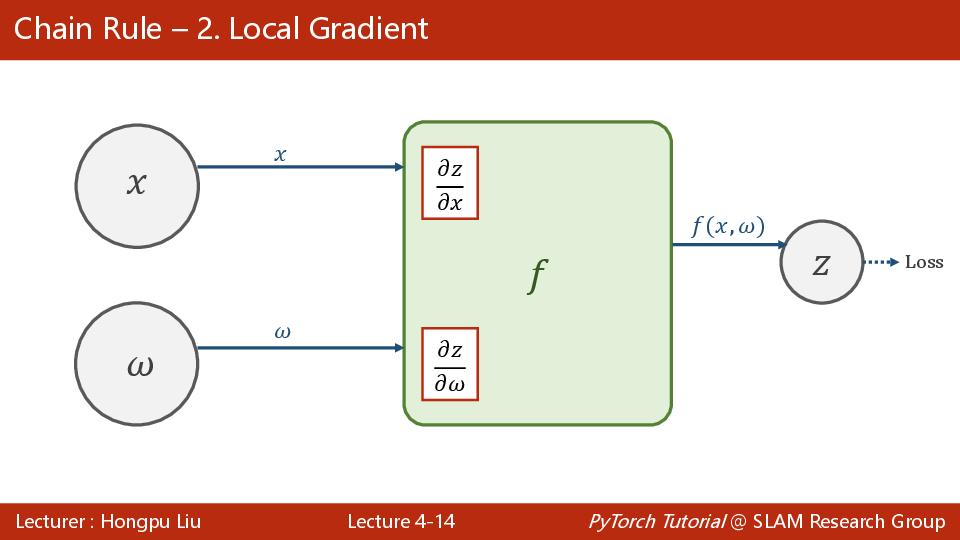
每个局部计算的导数,是在forward 构建计算图时就算好的,函数的梯度存储在各input节点上,而不是存在output节点上。
sigmoid function
Perceptron accepts several input signals and give one output, including 0 and 1. Each input times its corresponding weight and is added up. If the weighted summation is larger than threshold, the output is 1. Otherwise, output is 0.
深度学习一定要有偏置项Bias吗?外加一段简单的神经网络反向传播BP算法手写推导~ 一般要有 bias,因为线性函数 ax+b,b让模型在竖轴上移动,它在线性模型中是需要的。但在深度学习神经网络中,并不是每个地方都要设置 bias。 在清华大学的 cpm 项目中,认为在一些地方不设置 bias,使得模型训练稳定性会更强,计算速度以及显存消耗有优势