(2023-10-11)

一维高斯 数据 的空间分布像是一个中间重两头轻的铁棒 (线)； 二维高斯数据的分布像一个 椭圆 (面)； 服从三维高斯分布的数据的空间分布像一个 椭球 (体)。

Source video: 机器学习-白板推导系列(二)-数学基础

1. 高斯分布1-极大似然估计

P1

高斯分布在（统计）机器学习中非常重要。比如线性高斯模型是一整套体系，卡尔曼滤波就是一种线性高斯模型。 隐变量与隐变量，隐变量与观测变量之间服从高斯分布。

1
2
3

z1 -> z2 -> ... -> zN
↓     ↓      ↓     ↓
x1 -> x2 -> ... -> xN

比如从 z⁽ᵗ⁾ ➔ z⁽ᵗ⁺¹⁾ 的转移服从 线性高斯：z⁽ᵗ⁺¹⁾=Az⁽ᵗ⁾+B+ε，先做线性变换再加上 ε 高斯噪声。

再比如 P-PCA（概率PCA）中，原数据是 p 维的 x∈ℝᵖ 要降到 q 维空间 z∈ℝ^q， 假设 x 与 z 之间的变换为：x=Wz+μ+ε，ε～N(0,σ²⋅I)，0均值的各向同性的（即 Σ 是对角矩阵，并且对角线上的值都是σ²）高斯分布（标准正态分布）。 如果对角线上的值不相同，就变成了因子分析

而且线性高斯模型有很多特性：比如一个高维的随机变量 x∈ℝᵖ 服从高斯分布 x～N(μ,Σ)，将它分成两个小组 x₁∈ℝᵐ, x₂∈ℝⁿ, m+n=p。 则 x₁ 也服从高斯分布，条件概率 x₂|x₁ 也服从高斯分布。

参数估计

给定数据 𝐗：N个样本，每个样本 x 是 p 维的 x∈ℝᵖ，𝐗 就是一个 N x p 的矩阵：

𝐗 = (x₁, x₂,…, xₙ)ᵀ = $\[^{^{ x₁ᵀ}\_{x₂ᵀ}} \_{^{⋱}\_{ xₙᵀ}}]$ₙₓₚ

• $x_i \in \R^p$ : p维实数向量空间（p维欧氏空间），列向量

假设样本 xᵢ 之间是独立同分布，都是从一个高斯分布中抽出来的: xᵢ～N(μ,Σ)。

令参数 θ = (μ,Σ) （Σ是协方差矩阵：对角线上是σ²，μ 是位置参数，σ是尺度参数）

θ 的极大似然估计 (MLE)：θₘₗₑ = arg max_θ P(X|θ)

为简化计算：令 p=1 (一维)，则 θ = (μ,Σ=σ²)，一维高斯分布的概率密度函数: p(x) = 1/(√(2π)⋅σ) ⋅ exp(-(x-μ)²/2σ²)

高维（p维）的高斯分布的概率密度函数 (PDF)：p(x)=1/(2πᵖᐟ²⋅|Σ|¹ᐟ²) ⋅ exp(-½(x-μ)ᵀ⋅Σ⁻¹⋅(x-μ))

log P(X|θ) = log ∏ᵢ₌₁ᴺ p(xᵢ|θ) ，独立同分布，联合概率写成连乘
= ∑ᵢ₌₁ᴺ log p(xᵢ|θ) ，log把连乘变连加
= ∑ᵢ₌₁ᴺ log 1/(√(2π)⋅σ) ⋅ exp(-(xᵢ-μ)²/2σ²)，代入高斯分布
= ∑ᵢ₌₁ᴺ [ log 1/√(2π) + log 1/σ -(xᵢ-μ)²/2σ² ]

先求最佳的 μ:

当对数似然最大时，μ 等于多少？

μₘₗₑ = arg max_μ P(X|θ)
= arg max_μ ∑ᵢ₌₁ᴺ [ log 1/√(2π) + log 1/σ -(xᵢ-μ)²/2σ² ]
= arg max_μ ∑ᵢ₌₁ᴺ [ -(xᵢ-μ)²/2σ² ] ，只保留与μ相关的项
= arg min_μ ∑ᵢ₌₁ᴺ (xᵢ-μ)² ，σ² 一定是正的

对 μ 求偏导，令其等于0：

∂ ∑ᵢ₌₁ᴺ (xᵢ-μ)² / ∂μ = ∑ᵢ₌₁ᴺ -2(xᵢ-μ) = 0
∑ᵢ₌₁ᴺ (xᵢ-μ) = 0
∑ᵢ₌₁ᴺ xᵢ - ∑ᵢ₌₁ᴺ μ = 0
∑ᵢ₌₁ᴺ xᵢ = Nμ ，μ 与 i 无关

μₘₗₑ = 1/N ⋅ ∑ᵢ₌₁ᴺ xᵢ ，最优的 μ 就是样本的均值。 μₘₗₑ 是无偏的，因为 μₘₗₑ 的期望：

E[μₘₗₑ] = 1/N ⋅ ∑ᵢ₌₁ᴺ [μₘₗₑ]
= 1/N ⋅ ∑ᵢ₌₁ᴺ [ 1/N ⋅ ∑ᵢ₌₁ᴺ xᵢ ]
= 1/N ⋅ ∑ᵢ₌₁ᴺ [μ] ，因为样本iid,服从高斯分布
= 1/N ⋅ Nμ = μ (真实的 μ)

μₘₗₑ 的期望是无偏的，但每次的 μₘₗₑ 并不是真实的 μ，每次估出来的可能比μ大或者小，这个 μ 无法通过一次估计得到，只能是随着样本量的增加，把每次试验的结果求平均才会无限近似真实的 μ。 （但是样本不可能有无限个，所以实际上真实均值是无法得到的）

求最优的 σ²

用类似的过程:

σ²ₘₗₑ = arg max_σ² P(X|θ)
= arg max_σ² ∑ᵢ₌₁ᴺ [ log 1/√(2π) + log 1/σ -(xᵢ-μ)²/2σ² ]
= arg max_σ² ∑ᵢ₌₁ᴺ [ -log σ -(xᵢ-μ)²/2σ² ] ，只保留与σ²相关的项

目标函数对 σ 求偏导：

∂ ∑ᵢ₌₁ᴺ [ -log σ -(xᵢ-μ)²/2σ² ] / ∂σ = ∑ᵢ₌₁ᴺ [-1/σ - (xᵢ-μ)²/2 ⋅ -2σ⁻³ = 0 ，两边同乘σ³
∑ᵢ₌₁ᴺ [-σ² + (xᵢ-μ)² = 0 ，把∑ 带进去
∑ᵢ₌₁ᴺ σ² = ∑ᵢ₌₁ᴺ (xᵢ-μ)² ，σ² 与 i 无关
N σ² = ∑ᵢ₌₁ᴺ (xᵢ-μ)²

σ²ₘₗₑ = 1/N ⋅ ∑ᵢ₌₁ᴺ (xᵢ-μₘₗₑ)²

最优的 σ² 也是对样本方差求期望。 这个 σ²ₘₗₑ 是有偏估计，因为 σ²ₘₗₑ 的期望不等于 σ²：

先对 σ²ₘₗₑ 做简化:

σ²ₘₗₑ = 1/N ⋅ ∑ᵢ₌₁ᴺ (xᵢ - μₘₗₑ)²
= 1/N ⋅ ∑ᵢ₌₁ᴺ (xᵢ² - 2xᵢμₘₗₑ + μₘₗₑ²) ， 展开括号的平方
= 1/N ⋅ ∑ᵢ₌₁ᴺ xᵢ² - 1/N ⋅ ∑ᵢ₌₁ᴺ 2xᵢ⋅μₘₗₑ + 1/N ⋅ ∑ᵢ₌₁ᴺ μₘₗₑ²) ，∑带进去 = 1/N ⋅ ∑ᵢ₌₁ᴺ xᵢ² - 2μₘₗₑ² + μₘₗₑ² ，第2项里有个样本均值，第3项与i无关
= 1/N ⋅ ∑ᵢ₌₁ᴺ xᵢ² - μₘₗₑ²

对 σ²ₘₗₑ 求期望：

E[ σ²ₘₗₑ ] = E [ 1/N ⋅ ∑ᵢ₌₁ᴺ (xᵢ - μₘₗₑ)² ]
= E [ 1/N ⋅ ∑ᵢ₌₁ᴺ xᵢ² - μₘₗₑ² ]
= E [ 1/N ⋅ ∑ᵢ₌₁ᴺ xᵢ² -μ² - (μₘₗₑ²-μ²) ] ，添加μ² 横等变换
= E [ 1/N ⋅ ∑ᵢ₌₁ᴺ xᵢ² -μ²] - E [μₘₗₑ²-μ²] ，拆成2个期望

先看第 1 项： 把 μ² 写到 ∑ 里面： E [ 1/N ⋅ ∑ᵢ₌₁ᴺ xᵢ² -μ²] = E [ 1/N ⋅ ∑ᵢ₌₁ᴺ (xᵢ² -μ²)] ，μ²与i无关
= 1/N ⋅ ∑ᵢ₌₁ᴺ [E(xᵢ² -μ²)] ，里面是一个期望，把外面的期望展开
= 1/N ⋅ ∑ᵢ₌₁ᴺ [ E(xᵢ²) - E(μ²) ] ，μ²是常数
= 1/N ⋅ ∑ᵢ₌₁ᴺ [ E(xᵢ²) - μ² ] ，因为 μ 是随机变量 xᵢ 的期望：E(xᵢ)=μ
= 1/N ⋅ ∑ᵢ₌₁ᴺ [ E(xᵢ²) - E(xᵢ)² ] ，这是xᵢ 的方差（定义）
= 1/N ⋅ ∑ᵢ₌₁ᴺ σ²
= σ²

也就是说，第 1 项是 σ²，对于第 2 项： E [μₘₗₑ²-μ²] = E (μₘₗₑ²) - E(μ²) = E (μₘₗₑ²) - μ²
= E (μₘₗₑ²) - E²(μₘₗₑ)
= Var(μₘₗₑ) ，这是 μₘₗₑ 的方差
= Var( 1/N ⋅ ∑ᵢ₌₁ᴺ xᵢ ) ，把1/N 提出来，会变成平方
= 1/N² ⋅ ∑ᵢ₌₁ᴺ Var(xᵢ) = 1/N² ⋅ ∑ᵢ₌₁ᴺ σ²
= 1/N ⋅ σ²

所以 σ²ₘₗₑ 的期望等于上面两项相减： E[ σ²ₘₗₑ ] = σ² - 1/N ⋅ σ² = (N-1)/N ⋅ σ²

σ² 的无偏估计是 σ² = 1/(N-1) ⋅ ∑ᵢ₌₁ᴺ (xᵢ-μₘₗₑ)²

2. 高斯分布2-极大似然估计（无偏估计VS有偏估计）

P2

一个估计量 T(θ) 的期望 E(T(θ) 等于它的本身最初的值，这个参数的估计是无偏的，比如 E(μ^) = μ; E(σ^) = σ。如果不相等就是有偏的。

用MLE估计出来的方差 σ²ₘₗₑ 的期望小于模型的真实方差。 因为计算方差时，计算的是样本到样本均值 的距离，而不是到真实均值的距离，因为真实均值要做无数次试验才能得到（除非μ=样本均值）。 如果用样本均值代替真实均值μ 的话：Var(x)= E [(x-μ)²] ➔ Var(x)= E [( x-x̄ )]²，除非 μ=样本均值 x⁻，Var(x) = E( x-x̄ )² < E(x-μ)²。 证明如下样本方差与总体方差 - 小时候挺菜 -博客园：

(1/n)⋅∑ᵢ₌₁ᴺ(xᵢ-x⁻)² = (1/n)⋅∑ᵢ₌₁ᴺ [(xᵢ-μ)+ (μ-x⁻)]²
= (1/n)⋅∑ᵢ₌₁ᴺ (xᵢ-μ)² + (2/n)⋅∑ᵢ₌₁ᴺ(xᵢ-μ)⋅(μ-x⁻) + (1/n)⋅∑ᵢ₌₁ᴺ(μ-x⁻)²
= (1/n)⋅∑ᵢ₌₁ᴺ (xᵢ-μ)² + 2(x⁻-μ)(μ-x⁻) + (μ-x⁻)²
= (1/n)⋅∑ᵢ₌₁ᴺ (xᵢ-μ)² - (μ-x⁻)²

如果 μ ≠ x⁻，则 (1/n)⋅∑ᵢ₌₁ᴺ(xᵢ-x⁻)² < (1/n)⋅∑ᵢ₌₁ᴺ (xᵢ-μ)²

MLE 是点估计，会造成偏差

3. 高斯分布3-从概率密度函数角度观察

P3

多维高斯分布的概率密度函数: 对于一个 p 维的随机向量 𝐱∈ℝᵖ 服从多维的高斯分布，其概率密度函数为：

𝐱～N(𝛍,Σ)= 1/(2πᵖᐟ²⋅|Σ|¹ᐟ²) ⋅ exp(-½(𝐱-𝛍)ᵀ⋅Σ⁻¹⋅(𝐱-𝛍))， 其中μ 是期望, Σ是方差矩阵，exp里面-1/2后面是线代中的二次型

对于一个样本（随机向量）p个维度: 𝐱 = (x1,\ x2,\ …,\ xp)

𝛍 也是 p 维的向量：𝛍 = (μ1,\ μ,\ …,\ μp)

Σ 就是 p×p 维的矩阵：

Σ =(σ11, σ12, …, σ1p
σ21, σ22, …, σ2p
⋮ ⋮ ⋮ ⋮
σp1, σp2, …, σpp)

通常，这个矩阵Σ是半正定的，而且是沿对角线对称的，比如 σ12 = σ21。 在本节中假设 Σ 是正定的，以便叙述。

在 PDF 中，𝐱 是自变量，𝛍,Σ 是参数。式中与 𝐱 相关的只有 (𝐱-𝛍)ᵀ，其他部分认为是系数，所以集中看一下 exp 中的部分：

(𝐱-𝛍)ᵀ⋅Σ⁻¹⋅(𝐱-𝛍) 是一个标量，这个函数可以看作 马氏距离，两个向量：𝐱 和 𝛍 之间的距离

马氏距离

Mahalanobis distance is used to measure multivariate distances between a point and a normal distribution with covariance 𝚺. janakiev-blog

假设有两个二维的向量：𝐳1=(z11,\\ z12)，𝐳2=(z21,\\ z22)

根据定义求两向量之间的距离： (𝐳1-𝐳2)ᵀ ⋅ Σ⁻¹ ⋅ (𝐳1-𝐳2) = (z11-z21, z12-z22)ᵀ ⋅ Σ⁻¹ ⋅ (z11-z21, \\ z12-z22)

如果方差矩阵 Σ 是单位矩阵：Σ=I，马氏距离就是欧氏距离

(z11-z21, z12-z22)ᵀ ⋅ I ⋅ (z11-z21, \\ z12-z22) = (z11-z21)² + (z12-z22)²

方差矩阵

因为假设了 Σ 是正定的（每个特征值λᵢ都是大于0的，不能等于0），而且是对称的，所以对 Σ 做一个特征值分解：

Σ = UΛUᵀ，其中 U 是正交矩阵：UUᵀ=UᵀU=I，U=(𝐮₁,𝐮₂,…, 𝐮ₚ)，每个小 𝐮 是列向量，所以U是p×p的矩阵；Λ 是对角的：Λ=diag(λᵢ), i=1,…p；

把矩阵形式展开：

Σ = UΛUᵀ = (𝐮₁,𝐮₂,…, 𝐮ₚ) ⋅
(λ₁, 0, 0, … 0
0, λ₂, 0, … 0
⋮⋮⋮⋮
0, 0, 0, … λₚ) ⋅
(𝐮₁ᵀ,\\ 𝐮₂ᵀ,\\ …,\\ 𝐮ₚᵀ)
= (𝐮₁λ₁, 𝐮₂λ₂, …, 𝐮ₚλₚ) ⋅ (𝐮₁ᵀ,\\ 𝐮₂ᵀ,\\ …, 𝐮ₚᵀ)
= ∑ᵢ₌₁ᵖ 𝐮ᵢλᵢ𝐮ᵢᵀ

Σ⁻¹ = (UΛUᵀ)⁻¹ = (Uᵀ)⁻¹ Λ⁻¹ U⁻¹ = U Λ⁻¹ U⁻¹ ，（正交矩阵的转置等于它的逆），其中特征值矩阵 Λ⁻¹ = diag(1/ λᵢ), ᵢ=1,…,p
= ∑ᵢ₌₁ᵖ 𝐮ᵢ (1/λᵢ) 𝐮ᵢᵀ

把 Σ⁻¹ 代入马氏距离：

(𝐱-𝛍)ᵀ⋅Σ⁻¹⋅(𝐱-𝛍) = (𝐱-𝛍)ᵀ ⋅ ∑ᵢ₌₁ᵖ [ 𝐮ᵢ (1/λᵢ) 𝐮ᵢᵀ ] ⋅ (𝐱-𝛍) ，把(𝐱-𝛍) 放到 Σ 里面
= ∑ᵢ₌₁ᵖ [ (𝐱-𝛍)ᵀ ⋅ 𝐮ᵢ (1/λᵢ) 𝐮ᵢᵀ ⋅ (𝐱-𝛍) ]

定义一个向量 𝐲 = (y₁, y₂, …, yₚ)，其中每一维是一个标量：yᵢ = (𝐱-𝛍)ᵀ ⋅ 𝐮ᵢ 所以上面的马氏距离可以写成： (𝐱-𝛍)ᵀ⋅Σ⁻¹⋅(𝐱-𝛍) = ∑ᵢ₌₁ᵖ [ yᵢ (1/λᵢ) yᵢᵀ ]
= ∑ᵢ₌₁ᵖ [ yᵢ² (1/λᵢ) ] ， yᵢ 是标量，就是平方

假设 p=2，马氏距离= y₁²/λᵢ + y₂²/λ₂，而且令 马氏距离= 1: y₁²/λ₁ + y₂²/λ₂ = 1，就得到一个椭圆曲线

x1 和 x2 是原来的坐标轴，𝐮₁, 𝐮₂ 是新的基向量。把 xᵢ 变换成 yᵢ 就是向量 𝐱 减去均值之后（去中心化），然后投影到向量 𝐮ᵢ 上得到的坐标。

𝐱 和 𝛍 之间的马氏距离，在𝐮₁, 𝐮₂ 的坐标系下是一个椭圆曲线，不同的样本x对应曲线上不同的点。 如果 λ₁ > λ₂，则半长轴=√λ₁；半短轴=√λ₂

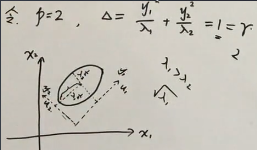
𝐱 和 𝛍 之间的马氏距离可以是任意值，即椭圆方程不等于1，取不同的值 r：

y₁²/λ₁ + y₂²/λ₂ = r

因为马氏距离是概率密度中的一项，马氏距离不同对应的概率就不同，r-> p(r)

当 r 取不同值的时候，就是一圈一圈的椭圆。对于一个两维的随机变量 𝐱=(x1,x2)，它的概率值y是第3维，所以在这个三维空间中，如果固定 y 值（即r值），就是对曲面水平横切了一刀，得到一条等高线，是在特征向量 𝐮 下的椭圆

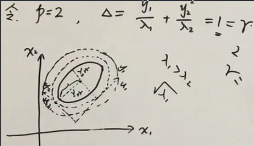
如果 Σ 分解出来的所有的特征值 λᵢ 都相同，曲线就变成圆了，在各个轴上的投影都相等。

4. 高斯分布4-局限性

P4

在高维高斯分布的概率密度函数中，只有 exp 里面的“二次型”与样本 x 相关，而且是𝐱 和 𝛍 之间的马氏距离， 对正定矩阵 Σ 做特征值分解，可以发现“二次型”对应于以特征向量 𝐮 为基底的坐标系下的标准椭圆曲线，

用 Δ 表示二次型，则概率密度函数：p(x)=1/(2πᵖᐟ²⋅|Σ|¹ᐟ²) ⋅ exp(-Δ/2)

在概率密度函数中，只有 x 是自变量，𝛍,Σ 都是模型的参数。 给定一个概率值 0 <= p(x) <= 1，比如 0.5，它会对应一个 Δ= r1，对应到椭圆方程的右侧，再把 r1 乘到左边就变成了标准的椭圆方程。 当 p=0.5, 则 Δ= r2，会得到另一个椭圆曲线。 如果把所有概率取一遍，就对应一个曲面。椭圆对应一条条等高线

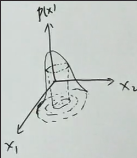
(1) 方差矩阵参数太多

Σₚₓₚ 有 p² 个参数，但又因为它是对称的，实际的参数个数= (p²-p)/2 + p = (p²+p)/2 = p(p+1)/2 = O(p²)

时间复杂度是维数的平方，在高维问题中，p 会很大，参数太多，计算太复杂。

可以简化方差矩阵：假设 Σ 是对角矩阵，只有对角线上有值 (λ₁ 0 0 … 0 \ 0 λ₂ 0 … 0 \ … \ 0 0 0 … λₚ)

因为它是对角矩阵（已经相互独立），就不需要对它做特征值分解了，Σ就用自己，没有引入新基向量 U=(𝐮₁,𝐮₂,…, 𝐮ₚ)，U就是单位矩阵，所以基向量还是 (𝐱₁,𝐱₂,…, 𝐱ₚ)，仍向𝐱投影 journeyc 的评论

Δ = (𝐱-𝛍)ᵀ⋅Σ⁻¹⋅(𝐱-𝛍) = ∑ᵢ₌₁ᵖ (𝐱ᵢ-𝛍ᵢ)² (1/λᵢ)

在各个轴上的投影为 yᵢ = (𝐱-𝛍)ᵀ ⋅ 𝐱ᵢ

所以这里的椭圆就是在 (𝐱₁,𝐱₂,…, 𝐱ₚ) 下的，长短轴与各x轴平行，而没有旋转

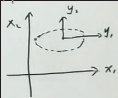
如果 ∑ 是对角阵，并且 λ₁ = λ₂ = … = λₚ，曲线就变成“正的”圆形，称为各向同性的高斯分布

通过简化方差矩阵，变成各向同性的，解决参数过多的问题。 比如在因子分析中，假设隐变量 z 是对角矩阵。概率PCA （P-PCA) 就是因子分析的特殊情况，假设 z 是各向同性的概率分布

(2) 一个高斯表达力有限

仅用一个高斯分布，对模型的描述可能不准确。GMM 是多个高斯分布的混合。

5. 高斯分布5-已知联合概率求边缘概率及条件概率

P5

已知一个多维高斯分布，求它的边缘概率分布，和条件概率分布

把 p 维的随机向量 𝐱 看作两组的联合：𝐱=(𝐱ₐ,\ 𝐱b)，其中 xₐ∈ℝᵐ, xb∈ℝⁿ, m+n=p。 把 p 维的期望 𝛍 也分成两组: 𝛍 = (𝛍ₐ,\ 𝛍b)； 把方差矩阵 ∑ 拆成 4 块：∑ = (∑ₐₐ , ∑ₐb \ ∑bₐ , ∑bb)，这是对称矩阵，所以∑ₐb = ∑bₐ

然后把随机向量 𝐱 看作是 (𝐱ₐ,𝐱b) 的联合概率分布，求边缘概率分布 P(𝐱ₐ)，以及条件概率分布 P(𝐱b|𝐱ₐ)。根据对称性，P(𝐱b) 和 P(𝐱ₐ|𝐱b) 也可求得

求解方法：配方法（PRML中），这节会采用一种比配方法稍微简单一点的方法

首先引入一个定理： 已知一个随机变量 x 服从高斯分布 x～N(μ,Σ)，有 y=Ax+B，则 y 也服从高斯分布： y～N(Aμ+B, AΣAᵀ)。 （x 是p维向量，y 是 q 维向量，则 A 是qxp 的矩阵，Σ是pxp的，则 AΣAᵀ 是qxq的）

不严谨的解释：

• E[y] = E[Ax+B] = AE[x]+B = Aμ+B

• Var[y] = Var [ Ax+B ] = Var [Ax] + Var [B] , B是常数方差=0
  = A Var [x] Aᵀ = AΣAᵀ

• 比如对一维随机变量 x～N(μ, σ²)，y=ax+b，则 Var[y] = Var[ax+b] = a²Var[x] = a²⋅σ²。直观上看，一维是a²，多维应该是AAᵀ

求边缘概率 P(𝐱ₐ) 的分布

构造一个矩阵： 𝐱ₐ = (Iₘ 0) (𝐱ₐ \ 𝐱b)

其中 (Iₘ 0) 对应 A，(𝐱ₐ \ 𝐱b) 就是 x，B=0

根据上述定理:

E[𝐱ₐ] = E[A𝐱+B] = A𝛍+B = (Iₘ 0) (𝛍ₐ,\ 𝛍b) = 𝛍ₐ

Var[𝐱ₐ] = AΣAᵀ = (Iₘ 0) (∑ₐₐ , ∑ₐb \ ∑bₐ , ∑bb) (Iₘ \ 0) = (Iₘ ∑ₐₐ, Iₘ ∑ₐb) (Iₘ \ 0) = ∑ₐₐ

所以 𝐱ₐ～N(𝛍ₐ, ∑ₐₐ)

求条件概率 P(𝐱b|𝐱ₐ) 的分布

（可用配方法）

构造3个变量：

1. 先定义一个 x_{b⋅a} 的变量：x_{b⋅a} = x_b - ∑_bₐ ∑ₐₐ⁻¹ xₐ 。 如果 x_{b⋅a} 的分布知道了 x_{b⋅a}～N(𝛍^, ∑^)，那么 x_b = x_{b⋅a} + ∑_bₐ ∑ₐₐ⁻¹ xₐ，x_b 与 xₐ 之间的关系就找到了。
   rationalizable 的评论：“如果能找到一个线性变换 Z = Xa+C⋅Xb，使得Z与Xb不相关 Cov(Z, Xb)=0，那么 Var(Xa|Xb) = Var(Z|Xb) = Var(Z)，E(Xa|Xb)=E(Z)-C⋅Xb，就都可以计算出来了。”

2. 与此对应，定义 𝛍_{b⋅a} = 𝛍_b - ∑_bₐ ∑ₐₐ⁻¹ 𝛍ₐ。

3. 因为 ∑ 是分块矩阵，把∑{bb⋅a} 定义为∑{aa} 的舒尔补Schur complement: ∑{bb⋅a} =∑{bb} - ∑{ba} ∑{aa}⁻¹ ∑_{ab}

(1) 先求 x_{b⋅a} 的分布:

x_{b⋅a} = (- ∑_bₐ ∑ₐₐ⁻¹, Iₙ) (xₐ,\\ x_b) = (- ∑_bₐ ∑ₐₐ⁻¹, Iₙ) 𝐱

所以 (- ∑_bₐ ∑ₐₐ⁻¹, Iₙ) 就是 A

E[x_{b⋅a}] = A𝛍+B = (- ∑_bₐ ∑ₐₐ⁻¹, Iₙ)⋅(𝛍ₐ,\\ 𝛍b) = 𝛍b - ∑_bₐ ∑ₐₐ⁻¹⋅𝛍ₐ = 𝛍_{b⋅a}

Var[x_{b⋅a}] = AΣAᵀ
= (- ∑_bₐ ∑ₐₐ⁻¹, Iₙ) ⋅ (∑ₐₐ , ∑ₐb \\ ∑bₐ , ∑bb) ⋅ ((-∑_bₐ ∑ₐₐ⁻¹)ᵀ,\\ Iₙ)
= (- ∑_bₐ ∑ₐₐ⁻¹, Iₙ) ⋅ (∑ₐₐ , ∑ₐb \\ ∑bₐ , ∑bb) ⋅ (-∑ₐₐ⁻¹ ∑_bₐᵀ, \\ I) ，其中 ∑ₐₐ⁻¹ 是对称的，转置没变

= (- ∑_bₐ ∑ₐₐ⁻¹ ⋅ ∑ₐₐ + ∑bₐ, -∑_bₐ ∑ₐₐ⁻¹ ⋅ ∑ₐb + ∑bb) ⋅ (-∑ₐₐ⁻¹ ∑_bₐᵀ, \\ I)

在第 1 项中，∑ₐₐ 是可逆，∑ₐₐ⁻¹ ⋅ ∑ₐₐ = I，然后 -∑_bₐ + ∑bₐ = 0：

= (0, -∑_bₐ ∑ₐₐ⁻¹ ⋅ ∑ₐb + ∑bb) ⋅ (-∑ₐₐ⁻¹ ∑_bₐᵀ, \\ I)

因为两个向量变量的协方差 Cov(X,Y) 与 Cov(Y,X) 互为转置矩阵，但它自身并不是对称矩阵，因此转置并不是它自己: ∑_bₐᵀ ≠ ∑_bₐ

= ∑bb - ∑_bₐ ∑ₐₐ⁻¹ ⋅ ∑ₐb ，就是定义的 ∑_{bb⋅a}

（弹幕：应该是根据舒尔补反向构造的 x_{b⋅a} 和 𝛍_{b⋅a}。“构造型证明”?）

所以得出结论： x_{b⋅a} ～ N(𝛍_{b⋅a}, ∑_{bb⋅a})

(2) 证明：x_{b⋅a} 与 xₐ 相互独立

专栏

若 x 为服从高斯分布的随机变量 x～N(μ,Σ)，则相互独立的两变量就不相关： M⋅x ⟂ N⋅x ⇔ M∑N =0。 其中 M，N 均为矩阵，M⋅x，N⋅x 也服从高斯分布。

证：因为 x～N(μ,Σ)，所以 M⋅x～N(Mμ, MΣMᵀ)，N⋅x～N(Nμ, NΣNᵀ)，计算二者的协方差矩阵：

Cov(M⋅x，N⋅x) = E[(M⋅x-M⋅μ) (N⋅x-N⋅μ)ᵀ]
= E[ M ⋅ (x-μ)⋅(x-μ)ᵀ ⋅ N]
= M⋅E[ (x-μ) (x-μ)ᵀ ]⋅N
= MΣNᵀ

因为 M⋅x ⟂ N⋅x 且均为高斯分布，所以 Cov(M⋅x，N⋅x) = MΣNᵀ = 0

在之前的推导中，引入了 x_{b⋅a} = x_b - ∑_bₐ⋅∑ₐₐ⁻¹ ⋅ xₐ 可以改写为：

x_{b⋅a} = (-∑_bₐ⋅∑ₐₐ⁻¹, I) (xₐ,\\ x_b)，这里 (-∑_bₐ⋅∑ₐₐ⁻¹, I) 对应 M，(xₐ,\\ x_b) 是 x

xₐ = (I, 0) (xₐ,\\ x_b)，这里(I, 0)对应 N，(xₐ,\\ x_b) 是 x

x_{b⋅a} 就是 M⋅x，xₐ 就是N⋅x， 所以 MΣNᵀ = (-∑_bₐ⋅∑ₐₐ⁻¹, I) (∑ₐₐ , ∑ₐb \\ ∑bₐ , ∑bb) (I,\\ 0)，其中∑是x的方差矩阵
= (0, ∑bb-∑_bₐ⋅∑ₐₐ⁻¹) (I,\\ 0)
= 0

所以 x_{b⋅a} 与 xₐ 相互独立可推出 x_{b⋅a} 与 xₐ 不相关： x_{b⋅a} ⟂ xₐ ⇒ x_{b⋅a} | xₐ = x_{b⋅a}

注意：

1. 一般情况下两个随机变量之间独立一定不相关，不相关不一定独立（也就是独立的概念更“苛刻”一点，不相关的概率稍微“弱”一点）
2. 如果两个随机变量均服从高斯分布，那么“不相关”等价于“独立”

随机变量独立是由分布函数定义的，而不相关只是用一阶矩（即数学期望）定义的。分布函数是比矩更高的概念，分布函数能决定矩，而矩未必能决定分布函数。 独立和互斥是什么关系？独立和不相关是什么关系？ - 武辰的文章 -知乎

(3) 再求 xb|xₐ 的分布

知道了 x_{b⋅ₐ} 的分布后，可知 x_b：

x_b = x_{b⋅a} + ∑_{ba} ∑ₐₐ⁻¹ xₐ

因为 x_b 与 xₐ 是相互独立的服从高斯分布的随机变量，所以：

x_b|xₐ = x_{b⋅a}|xₐ - ∑{ba} ∑ₐₐ⁻¹ xₐ | xₐ
= x_b = x{b⋅a} - ∑_{ba} ∑ₐₐ⁻¹ xₐ

还是同样套用Ax+B，把 x_{b⋅a} 看作 x, A=I, B=∑_bₐ ⋅ ∑ₐₐ⁻¹ ⋅ xₐ

E [x_b|xₐ] = 𝛍_{b⋅a} + ∑_bₐ⋅∑ₐₐ⁻¹⋅xₐ

Var [x_b|xa] = A⋅Var(x_{b⋅a})⋅Aᵀ = ∑_{bb⋅a}

所以 xb|xₐ ～N ( 𝛍_{b⋅a} + ∑bₐ⋅∑ₐₐ⁻¹⋅xₐ, ∑{bb⋅a} )

用同样的方法，可得 x_b～N(𝛍_b, ∑_{bb})。

P(xₐ|x_b) 就是把 P(xb|xₐ) 中的 a,b 对换。

6. 高斯分布6-已知边缘和条件概率求联合概率分布

P6

已知（边缘概率分布）p(x) = N(x | μ,Λ⁻¹) 和（条件概率分布）p(y|x) = N(y | Ax+b, L⁻¹) （其中 Λ 是精度矩阵=协方差矩阵 ∑ 的逆，Λ⁻¹=∑）， 并且假设 y 的期望与 x 之间有线性关系：μ_y = Ax+b，但二者的方差之间没关系 求 p(y)，p(x|y)。（类似于贝叶斯定理：p(x|y) = p(y|x)p(x) / p(y)）

这个问题经常在线性高斯模型中出现，比如在卡尔曼滤波中，隐状态（高斯分布）与观测变量之间有线性关系： z⁽ᵗ⁺¹⁾ = A z⁽ᵗ⁾ + B + ε，ε是噪声，ε～N(0,Q)，ε与z 相互独立， x⁽ᵗ⁾= Cz⁽ᵗ⁾+D+δ，δ也是高斯噪声 δ～N(0,R)

还比如在概率pca中，把 p 维的 x 降到 q 维的 z 空间，满足线性关系 x = Wz+b+ε，ε 是服从各向同性的高斯分布 ε～N(0, σ²I)，z 的先验可以是标准高斯分布 z～N(0,I)，ε 与 z 相互独立。也是一种线性高斯模型。

（在PRML 中仍使用配方法求解，而且比上一节的推导更复杂）

(1) 求 p(y)

依据两个前提条件，可以把 y 定义为： y = Ax + b + ε，令 ε 是一个高斯噪声 ε～N(0, L⁻¹)，x、y、ε 都是随机变量，ε和x相互独立，A和b 都是系数。 （y 是在 x 给定的情况下发生的，固定了x则它的方差为0，所以方差L⁻¹中不含 x 的方差）

E[y] = E[Ax + b + ε] = E [ Ax+b ] + E [ε] ，按照上一节引入的定理
= Aμ+b ，ε的期望是0

Var[y] = Var[Ax + b + ε] = Var[ Ax+b ] + Var [E]
= A⋅Λ⁻¹⋅Aᵀ + L⁻¹

所以就得到了 y 的分布： y～N(Aμ+b, A⋅Λ⁻¹⋅Aᵀ + L⁻¹)

(2) 求 p(z)

构造变量 z 是 x 和 y 的联合：z = (x,\ y)。 （“任意个有限维的高斯分布的联合分布均是高斯分布”，是说两个随机变量合起来的分布还是高斯，并不是GMM（对似然加权）正态分布随机变量的和还是正态分布吗？ - 江城雨-知乎。幽冥若炎的评论：不需要两个多维随机变量相互独立？x与y独立，因为x与ε独立）

根据上一节的结论，边缘概率分布就相当于仅仅考虑一部分维度，所以z服从的分布的期望和方差就是 x 的μ,∑ 与 y 的μ,∑ 拼起来：

E[z] = [μ,\\ Aμ+b]

Var[z] = [Λ⁻¹, unknown,\\ unknown, A⋅Λ⁻¹⋅Aᵀ + L⁻¹]

也就是： z = (x,\ y) ～ N ( [μ,\\ Aμ+b], [Λ⁻¹, unknown,\\ unknown, A⋅Λ⁻¹⋅Aᵀ + L⁻¹] )

因为方差矩阵本身应该是对称的，所以两个 unknown 是一样的，记为 Δ，它的最后结果里面不应该出现x 和 y。

Δ = Cov(x,y) = E[ (x-E[x]) ⋅ (y-E[y])ᵀ ]
= E [ (x-μ) ⋅ (y-(Aμ+b)ᵀ) ，把 y 的表达式代入
= E [ (x-μ) ⋅ (Ax + b + ε -Aμ -b)ᵀ)
= E [ (x-μ) ⋅ (Ax - Aμ + ε)ᵀ) ，两项里有共同的(x-μ)
= E [ (x-μ) ⋅ (Ax - Aμ)ᵀ + (x-μ) ⋅ εᵀ)
= E [ (x-μ) ⋅ (Ax - Aμ)ᵀ ] + E [ (x-μ) ⋅ εᵀ ]

因为 x 与 ε 独立：x⟂ε，所以 x-μ 与 ε 独立，所以第2个期望可拆开： E [ (x-μ) ⋅ εᵀ ] = E [ (x-μ) ] ⋅ E[ εᵀ ]，又因为 ε 的期望等于0，所以整项都=0，所以就剩第1项

Δ = E [ (x-μ) ⋅ (Ax - Aμ)ᵀ ]
= E [ (x-μ) ⋅ (x - μ)ᵀ ⋅ Aᵀ ] ，A不是随机变量
= E [ (x-μ) ⋅ (x - μ)ᵀ ] ⋅ Aᵀ，第1项是x的方差
= Var[x] ⋅ Aᵀ = Λ⁻¹ ⋅ Aᵀ

所以 z 的方差矩阵： Var(z) = [Λ⁻¹, Λ⁻¹ ⋅ Aᵀ,\\ Λ⁻¹ ⋅ Aᵀ, A⋅Λ⁻¹⋅Aᵀ + L⁻¹]

(3) 求 p(x|y)

根据上一节的结论：已知 x=(xₐ,\ x_b)，则有 P(x_b | xₐ) = N(𝛍_{b⋅a} + ∑_bₐ⋅∑ₐₐ⁻¹⋅xₐ, ∑_{bb⋅a})。

z 对应 x, xₐ,x_b 对应 x,y，z 的期望和方差已知，代入即可。

7. 不等式1-Jensen不等式

P7

比如在 EM 算法推导时，会用到此不等式

假设 f(x) 是凸 convex function 则该函数的期望大于等于期望的函数： E(f(x)) ≥ f(E(x))

(1) 证明

（以下是一个构造性证明）

有一个凸函数 f(x)，在 x 轴上取 x 的期望值 E[x]，它对应的函数值是 f(E[x])，过这个函数值做这个凸函数的切线，将这条切线定义为 l(x) = ax+b。

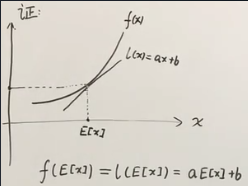
f(E[x]) = l(E[x]) = aE(x)+b

因为 f(x) 是凸函数，所以对于任意的 x 都有 f(x)≥l(x)，对此式两边同时求期望： E[ f(x) ] ≥ E [ l(x) ] = E[ax+b] = E[ax] + E[b] = aE[x] +b = f(E[x])

也就是 E[ f(x) ] ≥ f(E[x])

死神之名111 的评论： “第七节：很不幸，这个推导是错误的，你先说了f=l，你其实只说明了线性函数的jensen不等式成立，真正严格证明你需要做两个积分差，再利用凸性，二阶导＞0，综合一下就是当前结果。”

(2) 直观理解

通常的表述：在 x 轴上取两个点 a 和 b，然后在两点之间任意选取一个 c 点，选取时通常先在 [0,1] 上去一个 t 值，然后做“线性插值”：c=ta+(1-t)b。

f(a) 和 f(b) 连线为函数 g，则 c 的函数值为 g(c)，可以看到 g(c) ≥ f(c)

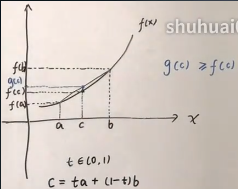
设线段ac 的长度是 t，线段 cb 的长度是 1-t（实际应该是ta 和(1-t)b），所以两梯形的斜边之比也是 t:1-t，

然后分别过 g(c) 和 f(a) 做水平线，形成相似三角形，则 f(b)-g(c) 与 g(c)-f(a) 之比是 1-t : t。

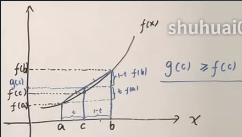
所以 g(c) = t ⋅ f(a) + (1-t) ⋅ f(b)

代入 g(c) ≥ f(c) 就是： t ⋅ f(a) + (1-t) ⋅ f(b) ≥ f(t⋅a+(1-t)⋅b)