SVM

• SVM本质上是一个判别模型，解决二分类问题，与概率无关
• 超平面: 𝐰ᵀ𝐱+b=0
  分类模型：f(𝐰) = sign(𝐰ᵀ𝐱+b)
• SVM有3宝，间隔对偶核技巧
  三大分类算法：
  1. Hard-margin SVM （硬间隔）
  2. Soft-margin SVM
  3. Kernel SVM

1 硬间隔SVM-模型定义（最大间隔分类器）

Video-P1

Hard-margin SVM

• 最大间隔分类器（max margin()）

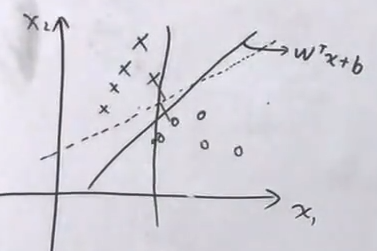
• 几何意义：对于平面上点的分类问题， 如果分界线两侧的点到线的距离很小，会对噪声很敏感，如果有一点噪声可能就被分到另一侧去了，泛化误差大。所以最好的分界线满足对所有点的距离都足够大。

  

• 从无限条可以正确分类的直线（超平面）中，选择最好的

• 数学表述：

  使间隔margin函数最大，实现对N个p维的样本点 ${(x_i, y_i)}_{i=1}^{N}, \quad x_i \in \R^p, y\in\{-1,1\}$正确分类

  $$ \begin{aligned} & \rm max , margin(\mathbf w, b) \

  & s.t. \begin{cases} \mathbf w^T x_i + b > 0, & y_i = 1 \ \mathbf w^T x_i + b < 0, & y_i = -1 \end{cases}

  \Rightarrow y_i(\mathbf w^Tx_i +b )>0, & \text{for $\forall$ i=1,…,N}（同号） \end{aligned} $$

• 每个点到直线的距离: $\rm distance(w,b,x_i) = \frac{1}{\| w \|} |w^T x_i +b|$

  $$ \begin{aligned} \rm margin(\mathbf w,b) & = \rm \underset{\mathbf w,b,x_i,i=1,…,N}{min}, distance(\mathbf w,b,x_i) \ & = \rm \underset{\mathbf w,b,x_i,i=1,…,N}{min}, \frac{1}{| \mathbf w |} |\mathbf w^T x_i +b|

  \end{aligned} $$

  • 因为限制条件 $y_i(\mathbf w^T x_i + b)>0$，而且$y_i=\{-1,1\}$，所以可以替换上式中的绝对值。
    所以最大间隔分类器可写为：

    $$ \rm \underset{\mathbf w,b}{max} \frac{1}{\| \mathbf w\|}\; \underset{x_i, i=1,...,N}{min} \; |\mathbf w^T x_i +b| $$

    (因为min只与$x_i$有关，而$\frac{1}{\| \mathbf w\|}$与$x$无关，所以移到了前面)

  • 对于限制条件 $y_i(\mathbf w^T x_i + b)>0$，说明存在最小值：

    $$ \exist \, r>0, \quad s.t.\; \rm \underset{\mathbf w,b,x_i,i=1,...,N}{min}\, y_i (\mathbf w^T x_i +b) = r $$

    所以可以继续简化：

    $$ \rm \underset{\mathbf w,b}{max} \frac{1}{\| \mathbf w\|} r $$

    因为超平面可以同比例缩放（$\mathbf{w^T x} + b = 2\mathbf{w^T x} + 2b$），所以可以设置最小值r为1，相当于把超平面缩放到1，系数乘在前面的$\frac{1}{\| \mathbf w\|}$里

    所以问题最终转化为一个凸优化问题：

    $$ \begin{cases} \rm \underset{w,b}{max} \frac{1}{| \mathbf w |} \ s.t. ; \operatorname{min} y_i (\mathbf w^T x_i + b) = 1 \end{cases}

    \Rightarrow

    \begin{cases} \rm \underset{w,b}{min} \frac{1}{2} \mathbf{w^T w} & \text{(目标函数是二次)}\ s.t. ; y_i (\mathbf w^T x_i + b) ≥ 1, ; i=1,…,N & \text{(N个线性约束)} \end{cases} $$

• 求解QP问题 (凸二次规划Quadratic programming问题)

  在维度不高，样本个数不多的情况下，比较好求解。 但是对于维度很高，样本很多，或者对数据$x$做$\phi(x)$的特征转换到了新的特征空间$Z$中，而Z的维度比原数据的维度高很多，就没办法直接求解，计算量太大。 借助拉格朗日乘子，引出它的对偶问题，求解相对容易的对偶问题。

  1. 把目标函数写成拉格朗日函数 $L$，把带约束问题化成无约束问题：拉格朗日函数只有对 λ 的约束，没有对 $𝐰$ 和 $b$ 的约束

     $$ L(\mathbf w,b,λ)= \frac{1}{2}\mathbf{w^Tw} + \sum_{i=1}^{N} \; \underbrace{λ_i}_{≥0} \; \underbrace{(1-y_i(𝐰^T x_i + b))}_{≤0} $$

     问题转化为：

     $$ \begin{cases} \rm \underset{\mathbf w,b}{min}\ \underset{λ}{max}\ L(\mathbf w,b,λ)\\ s.t. \; λ_i ≥0 \end{cases} $$

  2. 原问题的对偶问题：先对𝐰,b求L的最小值，再对 λ 求 L 的最大值

     $$ \begin{cases} \rm \underset{λ}{max}\ \underset{\mathbf w,b}{min}\ L(\mathbf w,b,λ)\\ s.t. \; λ_i ≥0 \end{cases} $$

     从直观上看，从最大值里面选的最小值一定是大于从最小值里面的最大值（省略证明）,也就是弱对偶关系：

     $$ \rm min\, max\, L ≥ max \, min\, L $$

     我们还想要强对偶关系，即 $\rm min\, max\, L = max \, min\, L$。对于凸二次优化问题，天生满足强对偶关系（证明略），原问题和它的对偶问题是同解的。所以直接求解对偶问题即可。

  3. 先固定 $λ$，对 $𝐰,b$ 求L的最小值，在此对偶问题中没有对𝐰,b的约束条件，所以是一个无约束的优化问题，直接求导：

     1. 先对b求导：

        $$ \begin{aligned} \frac{∂L}{∂b} &= \frac{∂}{∂b} \left[ \cancel{\sum_{i=1}^{N} λ_i} - \sum_{i=1}^{N} λ_i y_i(\cancel{\mathbf w^T x_i} + b)\right] \\ &= \frac{∂}{∂b} \left[ -\sum_{i=1}^{N} λ_i y_i b \right] \\ &= -\sum_{i=1}^{N} λ_i y_i =0 \end{aligned} $$

        把这个结果带入$L$

        $$ \begin{aligned} L(\mathbf w,b,λ) &= \frac{1}{2}\mathbf{w^Tw} + \sum_{i=1}^{N} ; λ_i ; (1-y_i(\mathbf w^T x_i + b))\ &= \frac{1}{2}\mathbf{w^Tw} + \sum_{i=1}^{N} \ λ_i - \sum_{i=1}^{N} ; λ_i y_i(\mathbf w^T x_i + b)\ &= \frac{1}{2}\mathbf{w^Tw} + \sum_{i=1}^{N} \ λ_i - \sum_{i=1}^{N} ; λ_i y_i\mathbf w^T x_i

        • \cancel{\sum_{i=1}^{N} ; λ_i y_i b} \

        \end{aligned} $$

     2. 再对$𝐰$求导，定义导数为等于0

        $$ \begin{aligned} & \frac{∂L}{∂𝐰} = \frac{1}{2} 2𝐰 - \sum_{i=1}^N λ_i y_i x_i ≔ 0 \\ & \Rightarrow 𝐰^* = \sum_{i=1}^{N} λ_i y_i x_i \end{aligned} $$

        把这个最优$𝐰^*$的表达式再带入$L$，就是L的最小值：

        $$ \begin{aligned} L(\mathbf w,b,λ) & = \frac{1}{2} \underbrace{ \left(\sum_{i=1}^{N} λ_i y_i 𝐱_i \right)^T}{\sum{i=1}^N λ_i y_i 𝐱_i^T } \sum_{j=1}^N λ_j y_j 𝐱_j

        • \sum_{i=1}^N \ λ_i y_i \left(\sum_{j=1}^{N} λ_j y_j 𝐱_j \right)^T 𝐱_i
        • \sum_{i=1}^N λ_i \ & = \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N λ_i λ_j y_i y_j \underline{𝐱_i^T 𝐱_j}
        • \sum_{i=1}^N λ_i y_i \sum_{j=1}^N λ_j y_j \underline{𝐱_j^T 𝐱_i}
        • \sum_{i=1}^N λ_i \ & = -\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N λ_i λ_j y_i y_j 𝐱_i^T 𝐱_j
        • \sum_{i=1}^N λ_i \ \end{aligned} $$

        所以对偶问题又化为：

        $$ \begin{cases} \underset{λ}{\operatorname{min}} ; \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N λ_i λ_j y_i y_j 𝐱_i^T 𝐱_j

        • \sum_{i=1}^N λ_i \ s.t. \ λ_i ≥0; \ \sum_{i=1}^N λ_i y_i =0 \end{cases} $$

  4. 固定 $\mathbf w,b$, 对于向量$λ$求$L$的最小值

     此时拉格朗日函数只与 $\lambda$ 有关

     求出 $\lambda$，根据 $\mathbf w = \sum_{i=1}^{m} \lambda_i y^{(i)} x^{(i)}$ 就可求出 $\mathbf w$，再根据 $b^* = -\frac{\rm max\ x_{i:y^{(i)}=-1} \mathbf w^{*T} x^{(i)} + min_{i:y^{(i)}} \mathbf w^{*T} x^{(i)}}{2}$，就可求出 $b$，最终得到分离超平面和分类决策函数。

KKT条件

• 原问题与对偶问题具有强对偶关系的充要条件就是满足KKT条件

  $$ \begin{cases} \frac{∂L}{∂𝐰} =0,\frac{∂L}{∂b} =0,\frac{∂L}{∂λ} =0 &\text{拉格朗日函数对w，对b，对λ 求偏导都等于0}\\ λ_i (1-y_i(𝐰^T x_i + b)) = 0 & \text{松弛互补条件slackness complementary} \\ λ_i ≥ 0 \\ 1-y_i(𝐰^T x_i + b)≤0 \end{cases} $$

• 由这些条件就可以求出最优解的$w^*$和$b^*$

  由 ∂L/∂𝐰 可求出𝐰∗=∑ᵢ₌₁ᴺ λᵢ yᵢ xᵢ

4 软间隔SVM-模型定义

Video-P4

Soft-margin SVM

• 允许一点点错误 loss

  $$ min \frac{1}{2} w^T w + loss $$

• loss函数:

  1. 违反约束条件的点的个数：$loss = \sum_{i=1}^N I \left\{ \underbrace{y_i (w^T x_i + b)<1}_{关于w不连续} \right\}$ （I是指示函数）

     不连续性： 令$z=y(\mathbf w^T \mathbf x+b)$，则 $loss_{0/1} = \begin{cases} 0, &\text{z<1} \\\\ 0, &otherwise \end{cases}$

     在z=1处有跳跃，不连续导致求导有问题。

  2. 用距离

超平面

• 能把 n 维欧式空间分成两部分的 n-1 维子空间。

  n 维空间 $\R^n$ 的超平面是由方程：$𝐰^T 𝐱 + b = 0$ 定义的子集。（𝐰 和 𝐱 都是n维向量）

• 法向量与超平面内任一向量垂直。假设在三维空间中，水平面内的一个向量 $𝐱-𝐱'$ 与法向量 $\mathbf w$ 垂直，如下图(源自如何理解超平面？)：

  

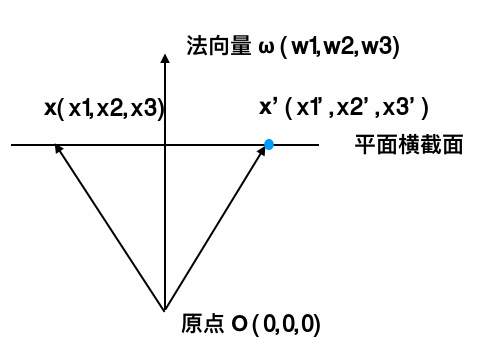
  满足：

  $$ \begin{aligned} (𝐱-𝐱')\mathbf w &= 0 \\ (x_1 - x_1', x_2 - x_2', x_3 - x_3') \cdot (w_1, w_2, w_3) &= 0 \\ x_1 w_1 + x_2 w_2 + x_3 w_3 &= w_1 x_1' + w_2 x_2' + w_3 x_3' \\ \mathbf w^T \mathbf x &= \mathbf w^T \mathbf x' \end{aligned} $$

  由于 $\mathbf w^T \mathbf x'$ 是常数项，$-\mathbf w^T \mathbf x' ≔ b$， 所以超平面的公式可写为：

  $$ \mathbf w^T \mathbf x + b = 0 $$

点到超平面距离

• 点到超平面的函数距离，除以法向量的范数

• 求平面外一点 $\mathbf x$ 到平面的距离 d。

  

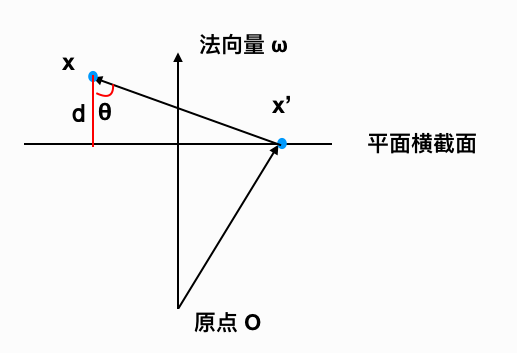
  根据三角函数：$cos \theta = \frac{d}{\| \mathbf x-\mathbf x' \|}$ (空间中一点向超平面作垂线，$\theta$只能是锐角，不必担心正负)

  $\mathbf x-\mathbf x'$ 与 $\mathbf w$ 的内积为： $|(\mathbf x-\mathbf x') \cdot \mathbf w | = \|\mathbf x-\mathbf x' \| \cdot \| \mathbf w \| \cdot cos \theta$ （因为法向量可能反向，所以给等式左边加上绝对值）

  联立可得：

  $$ d = \dfrac{|(𝐱 - 𝐱') 𝐰 |}{\| 𝐰 \|} = \dfrac{|𝐰𝐱 - 𝐰𝐱'|}{\| 𝐰 \|} $$

  因为 $𝐱'$在超平面内，$𝐰𝐱' = -b$，于是最后得到的任意点到超平面的距离公式：

  $$ d = \frac{|𝐰𝐱+b|}{\| 𝐰 \|} $$

几何距离与函数距离

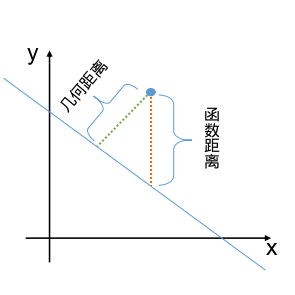
• 几何距离：点到直线（超平面）距离
• 函数距离：$Δy$，直线（超平面）上的点y=0，所以不在直线上的点到直线的函数距离就是点的y值。