Table of contents
1. 算法收敛性证明
Source video: P1
EM “期望最大” 用于解决具有隐变量的混合模型的参数估计,解决极大似然问题。 对于简单模型的参数估计问题,解析解可以直接求导得到,得不到解析解的用梯度下降或EM求数值解。
- X: random variable, observed data X={x₁,x₂,..xₙ} 各样本独立同分布iid
- θ: all parameters
- log P(X|θ): log-likelihood, 对数似然
用极大似然估计: θ_MLE = arg max_θ P(X|θ) ➔ arg max log P(X|θ)
对于含有隐变量的混合模型,直接求解析解非常困难,比如在 GMM (高斯混合模型)中,就很难写
EM迭代公式
- Z: Latent variable 隐变量也是随机变量,不同值有不同的出现概率
- (X,Z): Complete data 完整数据
- θ⁽ᵗ⁺¹⁾: t+1 时刻的参数
- P(Z|X,θ): Z出现的后验概率
- P(X,Z): X 和 Z 同时发生的联合概率。
- log P(X,Z|θ): 对数联合概率,对数完全数据
θ⁽ᵗ⁺¹⁾ = arg max_θ ∫_Z log P(X,Z | θ) ⋅ P(Z|X,θ⁽ᵗ⁾) dZ,(很像最大似然估计 log P(X|θ),只是这里的数据除了X还有隐变量Z,不用梯度下降而用迭代更新参数)
可以看作是按照 Z 的后验分布 (Z|X,θ⁽ᵗ⁾) 求对数联合概率的期望 (期望的定义-wiki):
-
第一步 Expectation:求对数完全数据 log P(X,Z|θ) 以后验 P(Z|X,θ⁽ᵗ⁾) 为概率密度函数的期望:
$E_{Z|X,θ⁽ᵗ⁾}[log P(X,Z|θ)]$ -
第二步 Maximization:找到期望最大时对应的参数作为下一时刻的参数:
$\rm θ⁽ᵗ⁺¹⁾ = arg\ max_θ E\_{P(Z|X,θ⁽ᵗ⁾)} [log P(X,Z|θ)]$
收敛性证明
(非严格)只证明一步,从 θ⁽ᵗ⁾ ➔ θ⁽ᵗ⁺¹⁾,似然会增大:log P(X|θ⁽ᵗ⁾) ≤ log P(X|θ⁽ᵗ⁺¹⁾),事件 X 在新一时刻的参数 θ⁽ᵗ⁺¹⁾ 所代表的概率模型下,发生的可能性变大了,不断迭代最后可取得最大 log-likelihood 对应的参数。
-
完全数据的似然:P(X,Z|θ) = P(Z|X,θ) P(X|θ),θ是起始值可以任意取
-
取对数:log P(X|θ) = log P(X,Z|θ) - log P(Z|X,θ)
-
两边关于 Z 的后验分布求积分(求对数似然的期望):
-
左边:
∫z P(Z|X,θ⁽ᵗ⁾)⋅log P(X|θ) dZ
= log P(X|θ) ∫z P(Z|X,θ⁽ᵗ⁾) dZ (似然与Z无关提到积分外面)
= log P(X|θ) (对Z的概率积分为1) -
右边:
∫z P(Z|X,θ⁽ᵗ⁾)⋅log P(X,Z|θ) dz - ∫z P(Z|X,θ⁽ᵗ⁾)⋅log P(Z|X,θ) dz
= Q(θ, θ⁽ᵗ⁾) - H(θ,θ⁽ᵗ⁾),分别分析两项Q 存在于EM迭代公式中,根据EM 的定义:θ⁽ᵗ⁺¹⁾ 对应最大的Q,所以: Q(θ⁽ᵗ⁺¹⁾, θ⁽ᵗ⁾) ≥ Q(θ, θ⁽ᵗ⁾) 是成立的。 上式的θ是初始值,若令θ = θ⁽ᵗ⁾,则 Q(θ⁽ᵗ⁺¹⁾, θ⁽ᵗ⁾) ≥ Q(θ⁽ᵗ⁾, θ⁽ᵗ⁾) 得证
因为 H 前面有个负号,所以要证 H(θ⁽ᵗ⁺¹⁾, θ⁽ᵗ⁾) ≤ H(θ⁽ᵗ⁾, θ⁽ᵗ⁾)
-
-
后 - 前时刻的 H:
H(θ⁽ᵗ⁺¹⁾, θ⁽ᵗ⁾) - H(θ⁽ᵗ⁾, θ⁽ᵗ⁾)
= ∫z P(Z|X,θ⁽ᵗ⁾)⋅log P(Z|X,θ⁽ᵗ⁺¹⁾) dz - ∫z P(Z|X,θ⁽ᵗ⁾)⋅log P(Z|X,θ⁽ᵗ⁾) dz
= ∫z P(Z|X,θ⁽ᵗ⁾)⋅log (P(Z|X,θ⁽ᵗ⁺¹⁾ / P(Z|X,θ⁽ᵗ⁾)) dz (合并)
= - KL( P(Z|X,θ⁽ᵗ⁾) || P(Z|X,θ⁽ᵗ⁺¹⁾)) (相对熵≥0)
≤ 0 -
(另一种证法) 用Jensen不等式,而不使用相对熵。
因为log是 concave (凹)函数:在曲线上任意取两个点,连成的直线小于log函数。concave函数的性质:a,b两点之间的一点c(两端点的线性组合)对应到直线函数上的值一定小于对应到log函数上的值
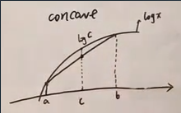
上面的合并为 1个log 之后的式子,可以看作是先求Z的后验的对数,再求"对数值"的期望,一定小于先求(自变量"Z的后验"的)期望再求对数:(E[log x] ≤ log E[x])
∫z P(Z|X,θ⁽ᵗ⁾)⋅log (P(Z|X,θ⁽ᵗ⁺¹⁾ / P(Z|X,θ⁽ᵗ⁾)) dz
≤ log ∫z P(Z|X,θ⁽ᵗ⁾)⋅(P(Z|X,θ⁽ᵗ⁺¹⁾ / P(Z|X,θ⁽ᵗ⁾)))
= log ∫z (P(Z|X,θ⁽ᵗ⁺¹⁾) dz = log 1 = 0
2. 迭代公式的导出
Source video: P2
EM 迭代公式来自于将对数似然 logP(X|θ) 分解为 ELBO + KL散度。
引入变量Z,则 P(X) 就变成了联合概率:P(X,Z|θ) = P(Z|X,θ)⋅P(X|θ), 所以对数似然就变为:
logP(X|θ) = log P(X,Z|θ) - log P(Z|X,θ)
引入 Z 的概率分布 q(Z):
logP(X|θ) = log P(X,Z|θ) - log q(Z) - log P(Z|X,θ) + log q(Z)
= log (P(X,Z|θ) / q(Z)) - log (P(Z|X,θ) / q(Z)),q(Z)≠0
技巧:对等式两边,按照分布 q(Z) 求似然的期望(积分):
-
左边:
∫z q(Z)⋅log P(X|θ) dZ = log P(X|θ)⋅∫z q(Z) dZ = log P(X|θ),q(Z)是概率密度函数积分为1,因此左边求完期望无变化,所以求似然 logP(X|θ) 就变成了求q(Z)。 -
右边:
∫z q(Z)⋅log (P(X,Z|θ)/q(Z)) dz - ∫z q(Z)⋅log (P(Z|X,θ)/q(Z)) dz
= ELBO + KL(q(Z) || P(Z|X,θ))
其中第1项:Evidence Lower Bound (ELBO,下界),第2项是Z的概率密度函数q(Z)与Z的后验概率P(Z|X,θ)的相对熵。因为 KL散度恒≥0,所以样本似然 log P(X|θ) ≥ ELBO。只有当 Z 的概率分布 q(Z) 与 Z 的后验分布 P(Z|X,θ) 相等时,KL散度等于0,似然=ELBO。
ELBO 是 log (P(Z,X|θ)/q(Z)) 按照 q(Z) 求期望(加权和;求积分)。当对数似然=ELBO,即达到最大时,q(Z)=P(Z|X,θ⁽ᵗ⁾),也就是先用上一时刻的θ⁽ᵗ⁾ 求出q(Z),然后ELBO里就只有log里的θ是变量,滑动调整θ使ELBO最大,取对应的θ作为θ⁽ᵗ⁺¹⁾。
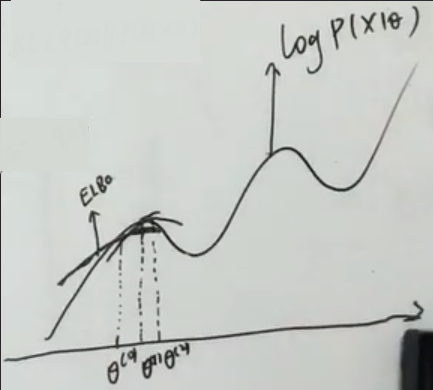
EM 想让 ELBO 达到最大,先(通过KL散度=0)找到样本对数似然 log P(X|θ) 的最大值对应的参数θ,作为新的θ,然后再算它对应的期望并得到ELBO, 取到最大值时的形式,即 ELBO,
然后取ELBO最大时对应的参数θ;
不断提高下界从而让对数似然 log P(X|θ) 也逐渐变大,最终ELBO等于logP(X|θ),KL散度=0,Z的概率分布与它的后验分布相等,
最优θ^ 是 ELBO 取最大时的θ
θ^ = arg max_θ ELBO
= arg max_θ ∫z q(Z) ⋅ log (P(X,Z|θ) / q(Z)) dz ,代换q(Z)
= arg max_θ ∫_Z P(Z|X,θ⁽ᵗ⁾) ⋅ log (P(X,Z|θ) / P(Z|X,θ⁽ᵗ⁾)) dZ
这个式子与 EM 的迭代公式相比,log 里多了一个分母:P(Z|X,θ⁽ᵗ⁾),展开log:
θ^ = arg max_θ ∫_Z P(Z|X,θ⁽ᵗ⁾) ⋅ [log P(X,Z|θ) - log P(Z|X,θ⁽ᵗ⁾)] dZ
= arg max_θ ∫_Z P(Z|X,θ⁽ᵗ⁾) ⋅ log P(X,Z|θ) dZ - P(Z|X,θ⁽ᵗ⁾) ⋅ log P(Z|X,θ⁽ᵗ⁾)] dZ
其中第2项与θ无关,因为 θ⁽ᵗ⁾ 是上一时刻的参数,是个常数,不是变量,而 log 中的 θ 是变量,会变到ELBO 取最大时对应的参数。所以就得到了迭代公式:
θ^ = arg max_θ ∫_Z P(Z|X,θ⁽ᵗ⁾) ⋅ log P(X,Z|θ) dz
3. 公式导出之ELBO+Jensen’s Inequality
Source video: P3
EM 迭代公式也可来自于将对数似然 logP(X|θ)分解为 ELBO + Jensen’s Inequality
Jensen’s Inequality 结论:对于一个凹concave 函数 f(x),在定义域x上取两点:a,b 连线小于a,b之间的函数值。
任意在 a,b 之间取一点 c = t⋅a+(1-t)b, where t∈[0,1],f(c)=f(t⋅a+(1-t)b) ≥ t⋅f(a) + (1-t)f(b)。
比如当 t=½ 时,f(a/2+b/2) ≥ f(a)/2 + f(b)/2,两边都是期望(平均数,加权和),简记为:先求期望再求函数值 大于等于 先求函数值再求期望,f(E) ≥ E[f]。当 f(x) 是常函数时,等号成立。
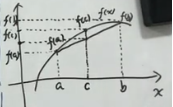
log P(X|θ) = log ∫zP(X,Z|θ) dz,在似然中引入隐变量 Z,然后求X的边缘概率,即对Z求积分(“把最终结果中不需要的事件合并成其事件的全概率而消失” marginal probability-wiki)
= log ∫z ( P(X,Z|θ) / q(Z)) * q(Z) dz,引入 Z 的分布 q(Z)
= log E_q(z) [P(X,Z|θ)/q(Z)],把积分看作求期望
≥ E_q(z) [ log(P(X,Z|θ)/q(Z)) ],Jensen不等式等号在 P(X,Z|θ) / q(Z)=C 成立, log C 是常函数
这个期望 E_q(z) [ log(P(X,Z|θ)/q(Z)) ] 就是对数似然的下界,就是ELBO。
q(Z) = P(X,Z|θ) / C
∫z q(Z) dZ = 1 = ∫z P(X,Z|θ) / C dZ = 1/C ∫z P(X,Z|θ) dZ = 1/C P(X|θ) (求边缘概率)
C = P(X|θ)
把 C 代换:q(Z) = P(X,Z|θ) / P(X|θ) = P(Z|X,θ)
所以当 Jensen 不等式取等号时,Z的分布 q(Z) 就是 Z 的后验分布P(Z|X,θ)。
所以 EM 第一步先按照上一时刻的参数 θ⁽ᵗ⁾ 和数据 X 求出 Z 的后验分布 P(Z|X,θ⁽ᵗ⁾), 再将对数似然 log(P(X,Z|θ)/P(Z|X,θ⁽ᵗ⁾)) 按照 Z 的后验分布求期望,得到对数似然的下界ELBO, 这个下界是关于 θ 的函数: ∫z P(Z|X,θ⁽ᵗ⁾)⋅log P(X,Z|θ) dZ,所以可找到这个下界最大时对应的θ,作为θ⁽ᵗ⁺¹⁾。不断迭代提高下界(期望),从而提高对数似然
4. 再回首
Source video: P4
EM 是解决优化问题的迭代算法(和梯度下降是一个level),而HMM,GMM 是模型
- 从之前狭义的(理想的)EM 推广到广义的(一般的)EM
- 狭义的EM 是广义EM 的一个特例
- EM 的变种
EM 主要用于概率生成模型,数据(随机变量)包括观测数据 X 及其对应的隐变量 Z,所以(X,Z) 叫做完全数据complete data,θ 是概率模型的参数。Z 是建模时引入的,Z生成了X,我们只能观测到X。 比如GMM 中,假设 z 是一个离散的分布,比如 K 个类别 z=1,2,…,K,每个类别都有一定的概率:
| 隐变量 z | 1 | 2 | … | K |
|---|---|---|---|---|
| 概率密度 | p₁ | p₂ | … | pₖ |
然后在 z 给定的情况下,x 满足高斯分布:P(x|z) ~ Gaussian,因此对完整数据 P(X,Z) 建模
还有 HMM 也可以从生成的角度来解释。比如 N 个隐变量: z₁, z₂, …, zₙ 是马尔科夫链的结构:
$$ s1 ➔ s2 ➔ ... ➔ sₙ \\\ ↧ \quad\ ↧ \quad ... \quad ↧ \\\ x1 \quad x2 \quad ... \quad xₙ $$可以把 z₁, z₂, …, zₙ 看成是统一的变量 Z,把 x₁, x₂, …, xₙ 看成是一个X
观测到了 X,假设它的概率模型的参数是θ,就可以用 EM 来估计参数 θ。
使用MLE 来估计参数:θ^ = arg max P(X|θ) = arg max ∏ᵢ₌₀ᶰP(xᵢ|θ) ➔ arg max log P(X|θ)
不能直接求解这个最大化问题的原因是,不知道P(X),因为样本X是非常复杂的,所以“会引入自己的归纳偏置,假定它是服从某个模型的。”
生成模型就是假设每个样本 x⁽ⁱ⁾ 都有一个隐变量 z⁽ⁱ⁾,x⁽ⁱ⁾ 是由 z⁽ⁱ⁾ 生成的,所以P(X) 就变成了联合分布 P(X,Z)(即把X分解处理),然后把 Z 积分掉就可以了: P(X) = ∫z P(X,Z) dZ
5. 广义EM
Source video: P5
EM 用于解决参数估计问题,优化函数使用 MLE ,找到让对数似然 log P(X|θ) 达到最大的参数 θ。 样本X 的分布 P(X) 未知,所以假设每个 x 是由隐变量 z 生成的。比如 GMM 假设 z 服从离散的概率分布,HMM 假设 z 满足马尔科夫链。然后 P(X) 就等于联合概率分布P(X,Z) 比上Z的后验分布P(Z|X),也就是未知X分布经过生成模型的假设,把问题具体化了。
因为 P(X|θ) = P(Z,X|θ) / P(Z|X,θ),所以(复杂的未知的)对数似然目标函数可分解为: 下界ELBO+Z的分布q(Z)与Z的后验分布P(Z|X,θ)的KL散度: log P(X|θ) = ELBO + KL(q||P)
ELBO 是一个期望,它和q(Z) 和 θ 有关,所以将其记为 L(q,θ); KL>=0, 当q=P时,KL=0,所以:log P(X|θ) ≥ L(q,θ),而且最优参数 θ^ 是在 q^= P(Z|X,θ) 时取到。
但是 q^ 并不一定能取到 P(Z|X,θ),因为这个后验可能是 intractable,是算不出来的。这由生成模型的复杂度决定, 如果生成模型比较简单,比如GMM的 z 和 HMM 的 z,他们是离散的,结构化的,是tractable,是可以(用EM)计算出来的
但是对于绝大多数的 z 是无法求出他的后验 P(z|x)。比如 VAE 的 z 是高维的,无法把它从 P(x,z) 中积掉,就得不到 P(x),也就无法(用贝叶斯公式)得到后验 P(z|x),所以最优的 q^(Z) 取不到,所以就需要变分(近似)推断:重参数化技巧+神经网络梯度下降用 q_ϕ(z|x) 逼近 P_θ(z|x)。
数学表达:
-
当 θ 固定 的时候,对数似然 log P(X|θ) 就是固定的,然后当 q(Z) 越接近 Z 的后验分布 P(Z|X,θ),KL散度就越小,同时 ELBO 就越大。所以求最优的分布 q(Z) 就变成一个优化问题: q^(Z) = arg min_q KL(q(Z) || P(Z|X,θ)) = arg max_q L(q,θ)
-
当 q^固定 的时候,再做极大似然找 θ,也就是做“狭义”的EM,最优的 θ^= arg maxᶱ L(q^, θ)
广义EM(两个最大化问题):
- E-step: q⁽ᵗ⁺¹⁾ = arg max_q L(q,θ⁽ᵗ⁾),固定θ求最优的q^
- M-step: θ⁽ᵗ⁺¹⁾ = arg maxᶱ L(q⁽ᵗ⁺¹⁾, θ),固定q^求最优的θ
对 ELBO 做变形(展开log):
L(q,θ) = E_q(z) [log (P(Z,X|θ)/q(Z))] = E_q(z) [ log P(Z,X|θ) - log q(Z) ]
= E_q(z) [log P(Z,X|θ)] - E_q(z) [log q(Z)]
= E_q(z) [log P(Z,X|θ)] + H[q(Z)]
其中第2项 H[q(Z)] 是分布 q(Z) 的熵: ∫ q(Z)⋅log (1/q(z)) dz , 所以 ELBO = 完全数据似然按照 q(Z) 求期望+ q(Z) 的熵
之前的EM 是广义EM 的一个特殊情况。对于 E-step, 狭义EM 默认 q 直接就取到了后验 P(Z|X,θ⁽ᵗ⁾),因为假定了后验能够求出。对于 M-step, 狭义EM 认为 q^ 已经找到了,那么广义EM 的M-step 中的熵就是确定值,要优化的只有似然。
6. EM 的变种
Source video: P6
(标准的,一般指的)广义的EM:对似然下界(ELBO联合概率按照z的后验求期望) L(q,θ) 求两次最大化,先固定θ⁽ᵗ⁾求q⁽ᵗ⁺¹⁾,然后固定q⁽ᵗ⁺¹⁾ 求 θ⁽ᵗ⁺¹⁾
因为两步都是求 Maximum,所以 EM 也称 MM (Maximation Maximation)
对于两个参数,先固定一个求另一个,再反过来,这种算法是坐标上升法,比如SMO。如果参数是多维的,固定其中某一个/两个,然后去求其他的。求参数的顺序没关系。
坐标上升法 与 梯度上升法并列
损失函数的等高线如下图,梯度上升法的参数路径是沿着梯度的,而坐标上升法类似曼哈顿距离,
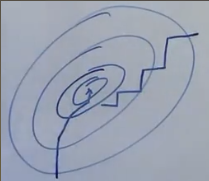
如果 E-step 中最优的 q^(Z),也就是Z 的后验P(Z|X,θ) 无法求得,就可以用变分推断求近似最优,比如基于平均场理论的变分法近似后验分布,再做 M-step,称这个组合为VBEM 变分贝叶斯EM。 如果用蒙特卡罗采样去求近似后验分布,叫作MCEM,蒙特卡罗EM。
VI(变分推断) 和 VB (变分贝叶斯)指的是同一个东西