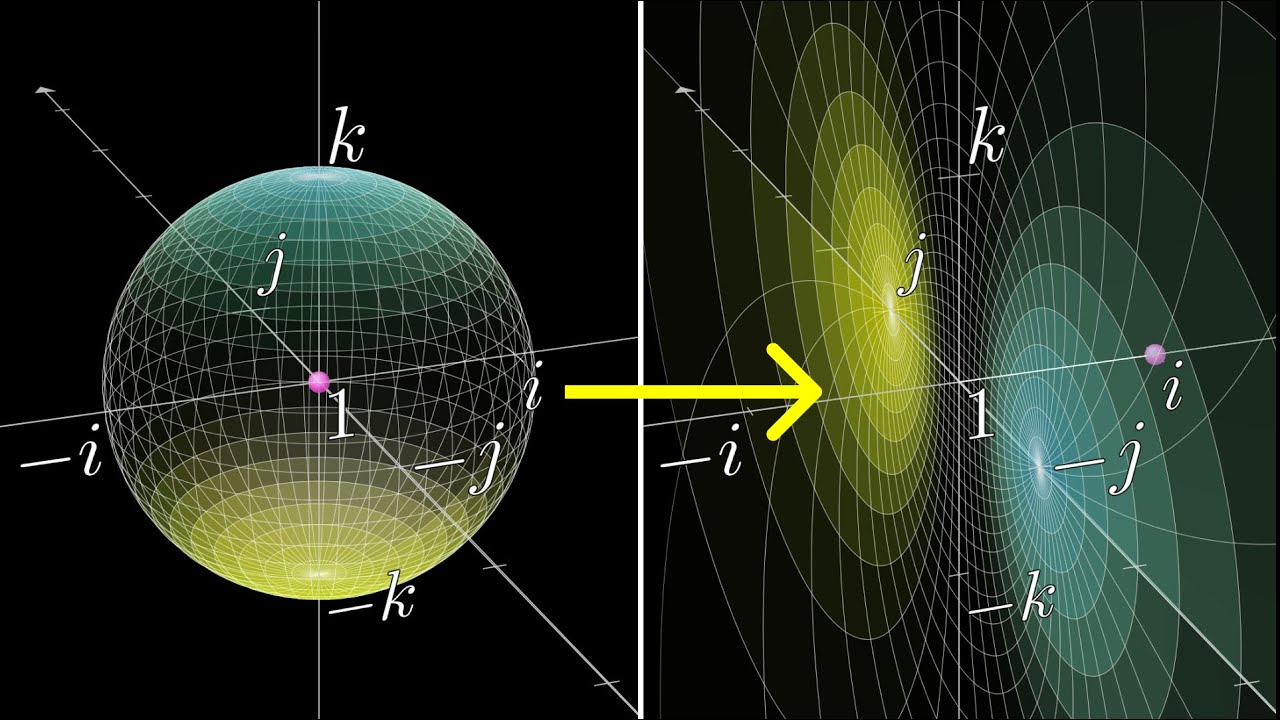
Stereographic Projection

Source video: Visualizing quaternions (4d numbers) with stereographic projection

Leveraging projection to reduce the dimensionality by 1. Such that quaternion in 4D space can be learned through the projection counterparts in 3D space.

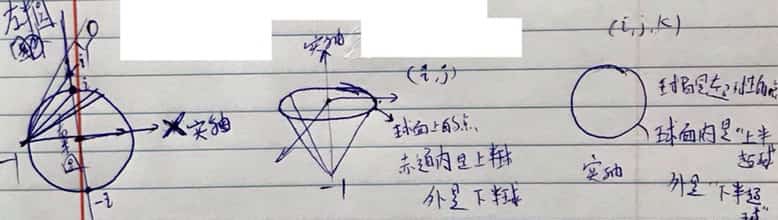
• 把 (i-实轴) 单位圆 做球极投影 stereographic projection 到 y 轴上:

  1. 从 x 轴的 -1 点出发过圆上每个点做射线，与 y 轴的交点即是圆上点的投影，

  2. 在这条投影线上，靠近 0 的点密集，越往外越稀疏，-i 和 i 是真实的圆上的点（代表着 x 为 0 的圆上点），(-i,i) 之间是右半圆的投影；

  3. 左乘 i 就是圆逆时针旋转 90 度，就是 1 ➔ i ➔ -1 ➔ -i 做一次循环移位。

• 把三维 (i-j-实轴) 单位球投影到水平面上:

  1. 从实轴的 -1 点出发连接球面上各点，与 i-j 平面交点即为投影点，

  2. 赤道是真实的球面上的点（代表着实部为 0 的三维复数），赤道之内是北半球的投影，之外是南半球的投影， 赤道两侧是对称的，极点附近的投影点密集；

  3. 左乘 i 就是球在 i 轴方向顺时针旋转 90°，赤道和零度经线共同在 1-i 平面内完成了一次 1 ➔ i ➔ -1 ➔ -i 循环移位， 乘以 j 就是球在 j 轴方向上顺时针，在 1-j 平面内完成一次 1➔ j ➔ -1 ➔ -j 循环移位

• 把四维 (i-j-k-实轴) 单位超球投影，

  1. 从实轴的 -1 点出发连接超球面上各点，与某个平面的交点形成一个个球面，每个球面就是每个四元数的投影，

  2. 在 i-j-k 空间的三维单位球是真实的超球面上的点（代表着所有实部为 0 的四元数）， 单位球内是实部为 0-1 之间的四元数的投影，负数实部的四元数被投影到了单位球外，实部=-1 的四元数在无穷远处(我们看不到)，

     我们能看到的投影点都有相同的模长（？不懂），四元数旋转时，就是三个维度共同移位，

     • (2023-11-07) 如果绘制出来的三维球代表 i,j,k 三个虚轴，那实轴就画不出来了，只能先固定它再分析。

  3. （把以上两种情况合起来:）i 是圆的球极投影，‘j+k’ 是球的球极投影， i 的移位顺序是 1,i,-1,-i，‘jk’ 的移位顺序是 j,k,-j,-k。 i 与 jk 满足右手定则：拇指指向 i，则四指卷曲方向就是 jk 旋转方向（拇指指向 j，k ➔ i ➔ -k ➔ -i 循环移位）

     

  四元数的可视化-3B1B + Krasjet评论

(2023-11-07)

3D Rotation

Because projection has been performed, the real axis is collapsed.

So when “rotating”，the real axis is fixed and only imaginary axes rotate.

Therefore, a 4-D quaternion can be used to describe the rotation in 3D space through its mutable 3 imaginary axes.

• Compared with Euler angles that define the hierarchical order of three angles, quaternion depicts the evolution of a single 4D vector.

Convert a quaternion to a 3x3 rotation matrix