Table of contents
RNN Cell
- 一个线性单元
- 把输入x的维度(inputSize)变换到 hiddenSize
- 处理带有时间序列的数据
- x2 与 h1 共同决定 h2
t时刻的输入 $x_t \in \mathbb R^3$ 经过 RNN cell 转换,变成了一个隐状态变量 $h_t \in \mathbb R^5$, 因此RNN cell是一个线性层(矩阵运算)映射到另外一个维度空间,不过这个线性层是共享的。
$h_t$ 会参与下次 RNN cell 计算 $h_{t+1}$,把之前的信息合并。 在计算 $h_1$ 时,需要输入先验 $h_0$,如果没有先验,就输入与 $h_1, h_2...$ 同维度的零向量。
遍历数据集 $x_t \in \mathbb R^{\rm input\_size}$,做线性变换
$$ W^{\rm hidden\ size \times input\ size}_{hi} xₜ + b\_{hi} $$变换到一个 hidden_size×1 的向量;
上一层的隐变量 $h_{t-1}$ 也进行线性变换 $W_{hh} h_{t-1} + b_{hh}$ 得到一个 hidden_size×1的向量, 它与 $x_t$ 的线性变换输出相加,得到的向量仍为 hidden_size × 1, 再做激活 tanh,算出隐向量 $h_t \in \mathbb R^{\rm hidden\_size}$
两个线性运算可以合一起:
$$ \begin{aligned} & W_{hh} h_{t-1} + W_{hi} x_{t} \\\ & = [W_{hh} \ \ W_{hi}]^{\rm h\ size \times (h\ size + i\ size)} \begin{bmatrix} h_{t-1} \\\ x_t \end{bmatrix}^{\rm (h\ size+i\ size) \times 1} \\\ & = h_t^{\rm h\ size \times 1} \end{aligned} $$$h_t = \rm tanh(W_{hi} x_t + b_{hi} + W_{hh}h_{t-1}+b_{hh})$
在Pytorch中,可以自己构造 RNN cell,并处理序列的循环;也可以直接使用RNN。
自己创建RNN Cell:
cell = torch.nn.RNNCell (input_size=i_size, hidden_size = h_size)
-
用 cell 计算下一时刻的隐变量:
h_1 = cell (x_1, h_0)。 -
这两个输入的 shape:x(batch_size, input_size),h(batch_size, hidden_size),
h_1的维度与h_0一样。batch是一批的样本条数。 -
数据集可以表达成一个张量:
dataset.shape = (seqLen, batch_size, input_size) -
使用RNNCell:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17import torch batch_size = 1 seq_len = 3 #有3个样本:x1,x2,x3 input_size = 4 #x都是4x1的向量 hidden_size =2 #h都是2×1的向量 cell = torch.nn.RNNCell( input_size=input_size, hidden_size=hidden_size ) dataset = torch.randn(seq_len, batch_size, input_size) #初始化h0,全零 hidden = torch.zeros(batch_size, hidden_size) for idx, input in enumerate(dataset): hidden = cell(input, hidden)
RNN class
实例化RNN:
cell = torch.nn.RNN(input_size = input_size, hidden_size=hidden_size, num_layer=num_layers)
RNN的输出有两个张量,调用:out, hidden = cell(inputs, hidden)。
inputs 是整个输入序列,输入的 hidden 是 $h_0$,out 是所有的隐层输出 $h_1 \cdots h_N$,输出的 hidden 是最后一个 cell 的输出$h_N$。
inputs 的形状是 (seqLen, batch, input_size),hidden 的形状是 (numLayers, batch, hidden_size),numLayers 是RNN的层数,每层最终都会输出一个隐变量。
output的形状为(seqLen, batch, hidden_size)。输出hidden与输入hidden的形状一样
|
|
Example: Seq ➔ Seq
例子: 序列 ➔ 序列,把“hello"转换到“ohlol”
把输入“hello”变成由数字构成的向量:
- 字符级别,为出现过的字符构造一个词典;
- 词级别,为出现过的单词构造词典。
这里为每个元素分配索引,用索引代替字母。再把每个索引变成一个向量(独热码),向量的长度与词典的条数一样
$$ \begin{aligned} \begin{bmatrix} h \\\ e \\\ l \\\ l \\\ o \end{bmatrix} \underset{\longrightarrow}{词典有4条索引} \quad \begin{bmatrix} 1 \\\ 0 \\\ 2 \\\ 2 \\\ 3 \end{bmatrix} \rightarrow \begin{matrix} [0 & 1 & 0 & 0] \\\ [1 & 0 & 0 & 0] \\\ [0 & 0 & 1 & 0] \\\ [0 & 0 & 1 & 0] \\\ [0 & 0 & 0 & 1] \end{matrix} \end{aligned} $$-
依次把 5 个独热向量输入 RNN,向量长度(input_size) = 4, output 是 5 个 RNN Cell的输出,每个输出对应于 4 个字母(h, e, l, o)中的一个,因此是一个多分类问题。
-
所以设置每个 hidden 是一个长度为 4 的向量,这 4 个线性输出分别对应(h,e,l,o)。 把这个向量传入 softmax就变成了一个概率分布,表示 4 个字母分别可能的概率。
-
再与真实标签的独热向量计算损失,即可用反向传播+梯度下降优化网络参数。
自己设计RNN Cell
|
|
调用pytorch的RNN类
|
|
独热向量在编码词/字符时:
- 独热向量维度太高,字符级别需128维,单词级别维度太高
- 向量太稀疏
- 是硬编码的
希望吧 单词/字符 联系到一个低维、稠密、从数据中学习到的向量,流行又强大的方法是嵌入层Embedding。把高维稀疏样本映射到低维稠密的空间(数据降维)。
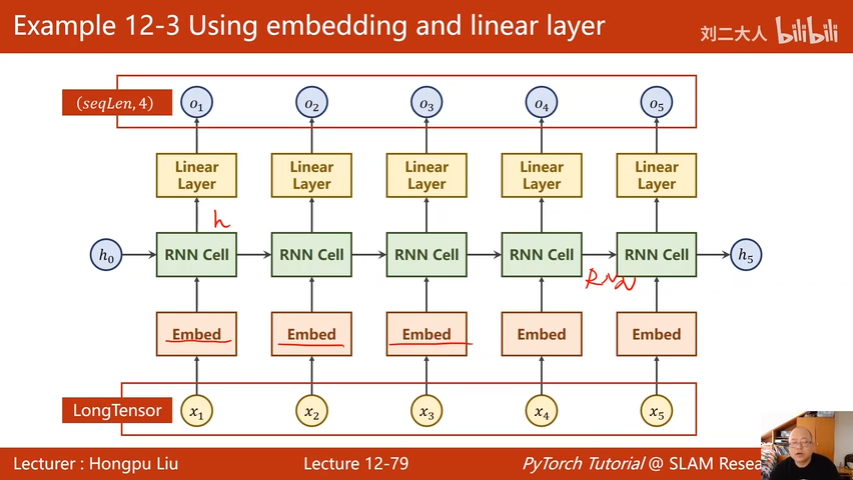
独热向量$x_n$通过嵌入层 Embed 变成稠密的表示,经过RNN线性变换后,再用一个线性层,让最后的隐变量输出与分类的数量一致
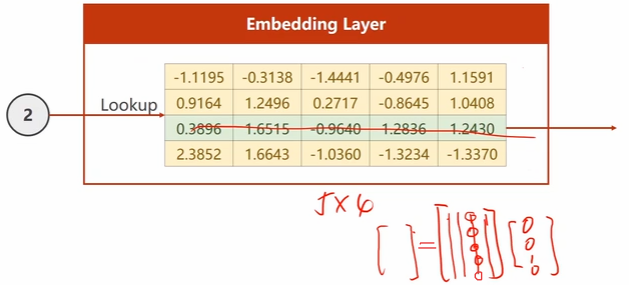
4维转5维,构建一个查找表:

查找表做转置,再乘以输入的独热向量,就可取出“对应行”
|
|
用RNN对MNIST图片分类
感觉里面的流程挺规范的。
- 初始化h0 为一个对角矩阵;
- 用了3层RNN,只用10个epoch就达到96%的accuracy了。
大概原理
把MNIST中每张图片看成一个序列,这个序列含有28个$x$(对应每一行像素),x的维度是28。每行像素都变换到一个h,这个h会参与计算下一行的h,最终得到第28行的h,将此h输入线性全连接层,变换到10维,每一维对应着0-9的每一类。然后这个10维的向量通过softmax,就是属于每类的概率了。
代码
|
|
k折交叉验证
返回第i折训练和验证数据
|
|
训练k次
|
|