Table of contents
(2022-12-28)
白板推导: VAE
Source video:【机器学习】白板推导系列(三十二) ~ 变分自编码器(VAE)】
VAE 和 GMM 一样也是生成模型:隐变量 z 生成观测变量 x,从而学习样本数据 x 本身的分布。不过 VAE 的 z 不是1维的,而是多维的。
-
用 EM 解 GMM 的最优参数 θ 时,假设 z 的后验分布 P(z|x;θ⁽ᵗ⁾) 能够取到,而且因为 z 是离散的,P(x) = ∑ₖ₌₁ᴷP(x,z=Cₖ;θ) 就能算出来, 所以后验 P(z|x)=P(x|z)P(z)/P(x) 也能算出来,其中分子两项是假设的分布。E步把目标函数: “最大的期望” $E\_{P(z|x)} [ log P(x,z|θ) ]$ 写出来,M步对其求导找出(期望最大时的)最佳θ⁽ᵗ⁺¹⁾。
-
而 VAE 的 z 是高维连续的,P(x) = $∫_z P(x,z) dz$ 积不出来,后验P(z|x) 就没法用贝叶斯公式导出,但可以用随机梯度下降变分推断(SGVI)近似后验。
-
“推断”是从 x 到 z 的过程:用样本 x 修正 z 的先验 P(z) 得到 z 的后验 P(z|x);而“生成”是从 z 的后验分布 P(z|x) 中采样出 z,再变换成样本的分布 P(x)。
flowchart LR; observed((x)) -->|Inference| latent((z)); latent -->|Generation| observed -
用 q(z|x;ϕ) 逼近后验 P(z|x;θ) 时,要最小化 $KL(q_{ϕ(z|x)} || P_{θ(z|x)})$,在 θ 固定,则似然 P(X) 也固定的情况下,等价于最大化 ELBO: arg max $E_{qᵩ(z|x)} [ log (P(z,x;θ)/qᵩ(z|x)) ]) ]$。类似广义 EM 的 E步,在 θ 固定的情况下,求后验的近似。
-
通过把联合概率拆开,这个 ELBO 也可写成: $E_{qᵩ(z|x)} [ log P(x|z;θ) ] - KL(q(z|x;ϕ) ||P(z))$。 当 z 的先验分布 P(z) 是标准正态时,那么KL散度就是希望 qᵩ(z|x) 的方差保持为I,不要太小,分布坍缩到一点就是过拟合:x与z一一对应,就变成 AE了,只能对训练样本 x 推出正确的 z。
-
求生成模型的最优参数 θ 同样是要使似然期望最大:arg max ELBO(x后验与KL散度同时优化),(没法直接求导)可采用梯度上升法,所以 VAE 是把 EM 的两步合起来了,既逼近后验 p(z|x) 的参数 ϕ,又逼近生成模型 p(x|z) 的参数θ。
-
在计算 ELBO 对 ϕ 的梯度时,∇ᵩL(ϕ) 可以写成一个期望,直接对 z 采样求均值可能由于方差太大而失效(而且采样操作不可导,就无法对z求梯度), 所以先对一个高斯噪声 ε 采样,再根据变换:z=μ_ϕ(x) + Σ_ϕ¹ᐟ²(x)⋅ε 得到 z (重参数化)。然后求均值(=梯度),带入梯度上升公式,更新ϕ。
-
训练NN时,输入一个 x,神经网络输出后验分布(编码)p(z|x) 以及采样出一个z。用这个z 通过另一个网络逼近 x 的后验分布(生成模型)p(x|z), 也就是在学到的 z 成立的情况下,从 p(x|z) 中采到 x 的概率,目标函数就是希望这个概率越大越好,可以假设 x服从二项或正态,把参数代入公式即得概率 或者说,分布 p(x|z) 的"众数" x’要与输入 x 的距离越小越好,当方差很小时,众数就是期望,即每次采样都会采到期望 μ(z),所以以 μ(z) 与 x 的距离作为目标函数。 一个x是多维的,它有自己(维度之间)的分布。
完整笔记:shuhuai008-32; 参考:隐变量模型到EM到变分自编码器 - 我要给主播生猴子 -知乎
(2022-12-29)
苏剑林: VAE(一)
Source article:变分自编码器(一):原来是这么一回事-苏剑林
通过隐变量 z 求样本 x 的分布:p(x) = ∫_z p(x|z) p(z) dz。 先学习 z 的后验分布 p(z|x)( 编码 ),再由它 生成 $\\^x$,$\\^x$应与x一样。
-
注意区分先验 p(z) 与后验 p(z|x)。因为假设了后验是正态分布的形式,所以是对 μᶿ,Σᶿ 做重参数化。而先验只出现在正则化项中,不参与后验的训练。
-
一个样本点x⁽ⁱ⁾对应一个(独立的、多元的)后验分布 p(z|x⁽ⁱ⁾),这样从中采出的 z 就一定对应这个样本点。所以每个样本有自己的正态分布。
-
z 是后验分布的一个采样,采样就会有偏差(方差),导致重构误差不为0。如果不加正则化,为了减小误差,Σ会不断减小到0,退化成AE。 从这个角度看 vae 是 AE 加上噪声,并约束噪声的强度(方差)尽量为1.
-
vae 希望所有的后验分布(”一般正态“)都与标准正态相似:μ=0,Σ=I,采样z时就保证了生成能力。因为各分量独立,所以是d维一元N的加和: KL( N(μ,Σ)|| N(0,I) ) = ½ Σ [(-logσ² + μ² + σ² -1) ]
-
重参数化技巧把服从N(μ,Σ)的随机变量 z 的概率拆成一个服从标准正态的变量ε和一个参数变换μ+ε×σ,从而实现虽然采样操作不可导,但它不参与梯度的反向传播。
-
条件VAE:样本属于不同的类别-期望不同 cvae代码:用2个线性层分别拟合μ和Σ,用重参数化技巧采样z,x与x’之间的重构损失用了交叉熵
model: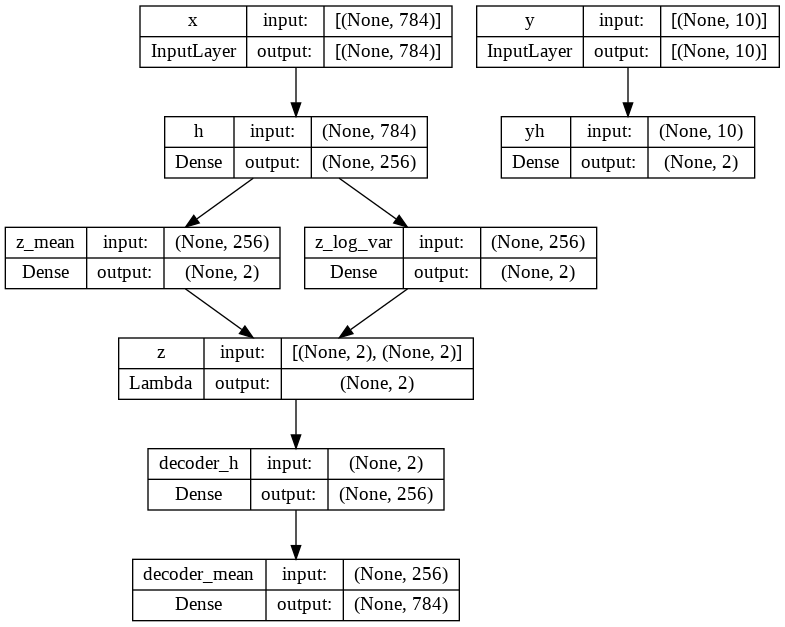
(2022-12-30)
苏剑林: VAE(二)
-
期望的数值计算与采样计算不同:数值计算是先给一个数列 x(其中$x⁰ < x¹ < x²<...xⁿ$),然后对里面的每个数 x⁽ⁱ⁾ 按它的概率加权求和:E[x]=∫ xp(x) dx。 但如果 x⁽ⁱ⁾ 是分布 p(x) 中的采样,概率大的会被多采几次,样本集合 x 中就包含了概率信息,不用再乘 p(x⁽ⁱ⁾)了:E[x]≈1/n⋅∑ᵢ₌₀ⁿ x⁽ⁱ⁾, x⁽ⁱ⁾∼p(x)
-
推导目标函数时,先构造了 p(x,z)=p(z|x)⋅p^(x),再构造 q(x,z)=q(x|z)q(z),这两个构造毫无关系,希望它俩互相靠近,而不是为了逼近z的后验p(z|x)。notes; (vae三-josh00的评论)
-
在生成阶段,若假设 p(x|z) 服从二项分布,则重构误差就是交叉熵;若假设 p(x|z) 服从正态分布,则重构误差就是MSE
-
训练时,生成阶段只从 z 的后验分布中采样一个,因为 z 是专属于一个x。P(x)➔ μ_ϕ(x), Σ_ϕ¹ᐟ²(x) ➔ z ➔ μ_θ(z) ➔ x'
(2022-12-31)
苏剑林: VAE(三)
-
vae生成时,只采一个z:因为x与z一一对应(自编码器)方差为0,vae引入了先验q(z)=N(0,I),方差也不会太大,也就是每次采样,结果都一样。如果直接做最大似然p(x|z),就需要从z的先验p(z)中采多个样本先估计出每个x的似然,再求似然的期望最大化。但如过没采到 zₖ,它对应的 xₖ的似然就是0,ln0是-∞,导致训练失败。
-
VAE 的重建生成相当于在AE上加了噪声(方差),所以可以生成与原始样本不同的数据。
%%{ init: { 'flowchart': { 'curve': 'linear' } } }%% flowchart TB x["x\n(样本)"] --> nn["隐变量的分布 μ(x), Σ(x)"] --> z --> nn2["数据的分布 p(x|z)\n 方差很小"] --> recon[x'\n重建样本] nn --> |"通过采样,从 “多个” 到 “一个”,
从 “无限” 到 “唯一”"| recon -
IWAE 对p(x,z)=∫p(x|z)p(z)dz 做等价变换,从而可从后验p(z|x)中采样z。
(2023-06-04)
PCA 与 VAE
They’re both learning the distribution of data.
DDG search: “PCA 与 VAE 对比”
Understanding Variational Autoencoders (VAEs) - Joseph Rocca
Variational Autoencoders explained — with PyTorch Implementation - Sanna Persson
|
|
Instead of mapping the input into a fixed vector, we want to map it into a distribution.
From Autoencoder to Beta-VAE - Lil’Log