Table of contents
(2022-05-08)
Condense math expression
Homogeneous coord 可以把 常数项 和 除法 引入矩阵运算,是为了把平移(加常数)和透视投影(除深度)写到一个矩阵中。 矩阵乘法就是先乘再加,当齐次坐标为1,用于添加常数项; 当齐次坐标不为1,可以作为系数被除掉,得到归一的xyz。
- Refer to 探秘三维透视投影-齐次坐标的妙用 -奇乐编程学院 bilibili
(2023-12-20)
-
使用齐次坐标,则非线性的透视投影可以写成线性的运算。
-
A linear operation T() satisfies additivity $T(a+b) = T(a) + T(b)$ and homogeneity $T(ca) = c T(a)$, where c is a scalar.
-
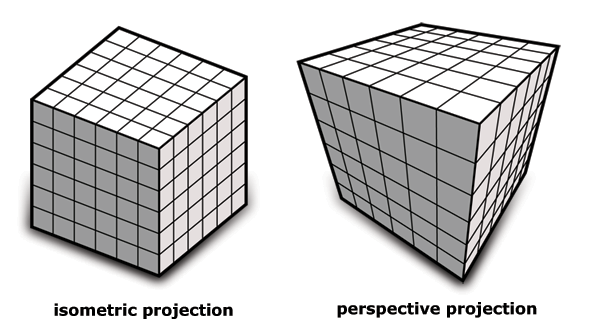
However, perspective projection 𝐏 for representing a 3D scene on a 2D plane requires x, y divided by depth: x/d, y/d. Intuitively, use scaling to indicate depth. Perspective projection will alter the shape, such as parallel lines are no longer parallel:
Parallel lines aren’t parallel after projection.
Similarly, the 2D projection of a 3D ellipsoid may not an ellipse with both ends of equal size, but a tapered oval, resembling the outline of an egg.
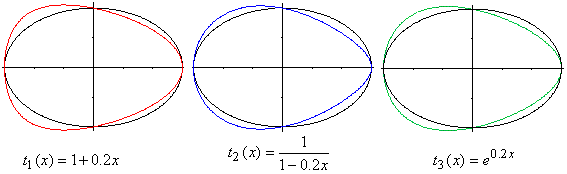
Ellipse vs oval
-
Perspective projection of a 3D Gaussian does not result in a 2D Gaussian. – Mathematical Supplement for the gsplat Library
-
-
Thus, 𝐏 is not linear.
-
But if we bypass the division by considering x, y are already divided by d, forming 2D plane coordiantes (x/d, y/d), and then multiplying by d again, the 2D coordinates (x/d, y/d) need to append an additional dimension, i.e., (x/d, y/d, 1), to record the multiplier d.
-
So, the 2D plane coordinates (x/d, y/d, 1) becomes (x,y,d) after multiplying with d.
$$(u,v) = (u,v,1) = (x/d, y/d, 1) = (x, y, d)$$Note: Appending 1 is not trying to revert a 2D pixel to 3D space, but used to represent the one more operation for the 2D coordinates. So it still represents a 2D pixel after appending 1.
-
That means, during the intermediate computation, there is no need to calculate (x/d, v/d) to obtain (u,v) , but use (x, y, d) to refer a 2D plane coordiantes.
In summary, the division is skipped, and 𝐏 becomes a linear operation represented with a 3x3 matrix.
-
When moving in 3D space, the 3D coordiantes (x,y,z) needs an extra dimension as (x,y,z,1) to combine rotation and translation together. And [R|t] is a linear operation.
-
(2024-02-15) The projection matrix also applies to a 4D camera point (x,y,z,1), where the homogeneous coordinate 1 will store the z, after the camera point got multiplied by the projection matrix, where the 4-th row is [0 0 -1 0].
As the resulting clip coordinates are not the final transformation yet in the pipeline, the original depth $z$ in camera space requires to be recorded for the perspective division that is supposed to be the final step.
After frustum clipping and the clip coordinates perform perspective division, ND coordinates are obtained and utilized in the ND space for image formation.
-
-
(2024-01-01) Summarize again
In the perspective projection, homogeneous coordinates use 3D coordinates to represent a 2D pixel for temporarily storing the depth value, which will be divided at the very end to keep the intermediate computations as linear operations.
Moreover, in the view transformation, homogeneous coordinates uses 4D coordinates to represent a 3D point for holding the translation vector.
-
(2024-07-18)
-
齐次坐标的作用:
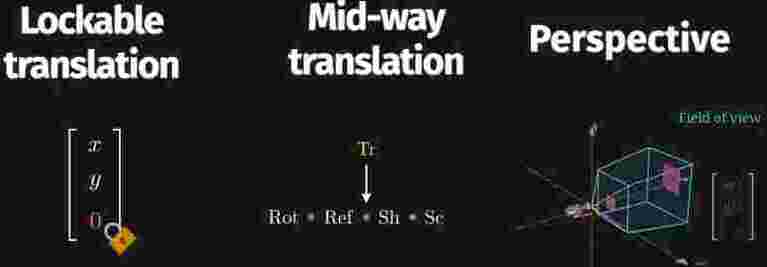
Image from Quick Understanding of Homogeneous Coordinates for Computer Graphics - Miolith 中文翻译: 计算机图形学快速理解:齐次坐标 - Miolith)
(2024-07-21)
- 透视除法的根源是相似三角形:$\frac{x_{film}}{focal} = \frac{X_{cam}}{Z_{cam}}$。
(2022-08-16)
Distinguish point and vector
齐次坐标用于区分 向量 和 点。‘向量’只需基向量的线性组合,而’点’需要加上原点,把’点’表示为从原点出发的向量。 给定一组基向量𝐱,𝐲,𝐳,则一个向量𝐯 = a𝐱+b𝐲+c𝐳;而一个点 𝐩 = 𝐨+a𝐱+b𝐲+c𝐳,其中𝐨是原点。所以(a,b,c,0)是向量𝐯的坐标,而(a,b,c,1) 是点𝐩的坐标。
平移变换需要使用齐次坐标,是因为只有‘点’需要平移,要想表示点就得用齐次坐标。而向量没有位置的概念,只有大小和方向
- Refer to 深入探索透视投影变换 - popy007 -CSDN
-
(2024-02-17) Tutorial 3 : Matrices - opengl-tutorial.org
(x,y,z,w=1) is a position, while (x,y,z,w=0) is a direction.
(2023-02-13)
Show 3D world on a plane
When the homogeneous coordinate w=1 is appended behind the Cartesian coordinates (u,v), the result (u,v,w=1) becomes the 3D point (x,y,depth) because u=x/depth, v=y/depth.
 2D world on plane |
 3D world on plane |
For example, the railroad tracks are parallel on the 2D ground plane.
But when they’re observed in a (higher-dimension 3D) projective space (human eyes, camera, convex lens), the parallel lines would converge.
Otherwise, if our eyes are plane mirror, we will never find the world is 3D.
This effect can be interpreted as that the coordinates (x,y) scale down as 3D points get further away. Hence, drawing a railroad onto canvas should follow th relationship: (x/depth, y/depth), where x,y are constants and the depth increases.
2D plane can only represent 2 directions, so if we want to display 3D world on a 2D plane, the additional dimension (depth) has to be engaged implicitly.
Therefore, the meaning of pixel (u,v) on plane is (x/depth, y/depth), which corresponds to the 3D point (x,y,depth), such that the picture mimics the scene looked at by human: x,y are inversely proportional to depth (Big near, small far: perspective).
The homogeneous coordinate w=1 is used to accommodate the depth:
(u = x/depth, v = y/depth, w=1) ⇒ (x, y, depth).
The w is not specified arbitrarily. If the given 2D coordinates are (u,v), then the w should =1, waiting for the depth split from u,v.
Therefore, an extra dimension is supplimented to adapt the observation from higher-dimension space.
Then, the homogenous coordinates of a pixel (u,v) on the plane is (u,v,w). When analyzing it in 2D space, its coordinates are (u/w, v/w).
For example, two pixels represented by homogeneous coordinates are (1,2,1) and (1,2,0)
That is, the projection pixel (u,v) of a 3D point, when the point goes far away, the coordinates (u,v) are not constant but inversely changing with depth.
This effect can be represented by an extra dimension to reflect the depth change.
(2023-02-12)
Compensate for Cartesian coord
The homogeneous coordiante w is supplemented to adapting Cartesian coordiantes to represent projective space Homogeneous Coordinates - songho. (Cannot convince me)
-
The parallel lines should never intersect at infinity in Cartesian space (plane), but they have to converge in projective space (human eye/camera).
-
To use 2D planes to represent perspective, the homogeneous coordinate w is appended behind the Cartesian coordinates (x,y) of each point to adapt to the projective observation.
-
Thus, each point in projective space has 3 coordinates (x,y,w). Then, the 2D coordinates of each point are obtained by normalizing the 3rd dimension: (x/w, y/w, 1), such that two parallel lines would converge.
In other words, it’s easier to analyze multiple points by scaling their w to 1. -
Homogeneous coordinate w is the auxiliary for the Cartesian space. Thus, the effect of depth can be represented on a plane (like projection).
-
If the point (1,2) from Cartesian space is combined with different w to make up the homogeneous coordinates (1,2,w), the corresponding 2D coordinates (1/w, 2/w) will form a line.
-
If the 3 coordinates change propotionally, like (1,2,3), (2,4,6), … (n,2n,3n), these homogeneous coordinates corresponds to a common 2D coordinates (1/3, 2/3) on the plane. This means the homogeneous coordinates are scale invariant.
Or inversely, a pixel on the plane corresponds to a line in the 3D space (homogeneous coordinates system). -
w is an attribute for each point in perspective space, where every point has 3 coordinates (x,y,w), while the points in Euclidean space don’t have this property. -
What we human perceived on our retina or captured on the camera plane are the projection: (x/w, y/w, 1).
-
Because each 3D point has differnt w, their projections are located on different position on the image plane. Thus,
-
Therefore, given an image, the homogeneous coordinates for each pixel are (u/w, v/w, 1).
If the w is known, then the homogeneous coordinates can be wrriten as (u, v, w).
The point in 3D space has the coordinates: (x,y,w) is divided by the w. homogeneous coordinates (x,y,w)
A picture showing projective effect actually is a stack of different planes with different depth.
(x/w, y/w), where the x,y are already divided by the dpeth w, so if we want to get the Cartisan coordiantes back, the w has to be separated: (x, y, w), then the first 2 number are 2D Cartesian coordinates.
That means the homogeneous coordiantes of 2D point (x,y) is just appending a w at the end, like (x,y,w).
- The points with propotional homogeneous coordinates corresponds to the same 2D Cartesian point. For example, (1,2,3) and (2,4,6)
With the extra dimenstion, the coordinates for a 2D pixel
Homogeneous coordinates convert the non-homogeneous linear system to a homogeneous system.
- If the homogeneous coordinate w added behind Cartesian coordinates is to represent the depth (x/w,y/w,1)ᵀ, then the homogeneous coordinate w=1 added behind a 3D points is to accommodate the translation (x/w, y/w, z/w, 1)ᵀ.