P4

3D Transformations

3D Scale

3D Translation

Rotaion around axises

• 绕x轴旋转：
  x方向坐标不变，所以旋转矩阵各列向量的x分量都不贡献，所以第一行是1 0 0；
  为了保证逆时针旋转是正向旋转，其余两轴的顺序如图：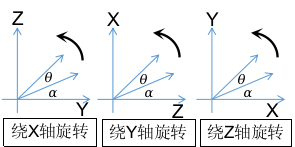
  

  

  y-z平面旋转，用待定系数法或展开三角函数，可得旋转关系为： $\begin{cases} x'=x \\\\ y'=ycosθ-zsinθ \\\\ z'=ysinθ+zcosθ \end{cases}$，
  则旋转矩阵为 $\begin{pmatrix} x' \\\\ y' \\\\ z' \end{pmatrix} = \begin{pmatrix} 1&0&0\\\\ 0 & cosθ & -sinθ \\\\0 & sinθ & cosθ \end{pmatrix} \begin{pmatrix} x\\\\y\\\\z\end{pmatrix}$；
  写成齐次坐标，不考虑平移，所以仿射变换矩阵为：

  $$ R_x(α)= \begin{pmatrix} 1 & 0 & 0 & 0 \\\ 0 & cosθ & -sinθ & 0 \\\ 0 & sinθ & cosθ & 0 \\\ 0 & 0 & 0 & 1 \\\ \end{pmatrix} $$

• 绕y轴旋转：
  y方向不变，所以矩阵第2行为：0 1 0；
  x-z平面旋转，用待定系数法，可得旋转关系： $\begin{pmatrix}z'\\\\x' \end{pmatrix} = \begin{pmatrix}cosθ& -sinθ\\\\sinθ & cosθ\end{pmatrix} \begin{pmatrix} z\\\\x \end{pmatrix}$
  (或者展开三角函数，可得旋转关系为： $\begin{cases} x'=zsinθ+xcosθ \\\\ z'=zcosθ-xsinθ\end{cases}$)
  写成旋转矩阵为：

  $$ \begin{pmatrix} x' \\\ y' \\\ z' \end{pmatrix} = \begin{pmatrix} cosθ & 0 & sinθ \\\ 0 & 1 & 0 \\\ -sinθ & 0 & cosθ \end{pmatrix} \begin{pmatrix} x \\\ y \\\ z \end{pmatrix} $$

  三个轴循环对称：$x\boxed{yzx}y\boxed{zxy}z\boxed{xyz}$，即给定任意两个可得后面一个，所以Y是由$Z×X$的到的 $\begin{pmatrix}Z\\\\ X\\\\ Y\end{pmatrix}$，这与通常书写 矩阵顺序$\begin{pmatrix}X\\\\ Y\\\\ Z\end{pmatrix}$不同，导致系数易位，$-sinθ$不在左上角，看起来与绕其他两轴的旋转矩阵不一致。

• 绕z轴旋转：
  z方向不变，所以矩阵第3行为：0 0 1；
  x-y平面旋转，有旋转关系 $\begin{cases}x'=rcos(α+θ)\\\\y'=rcos(α+θ)\end{cases}$ 以及 $\begin{cases}x=rcosα\\\\y=rsinα\end{cases}$
  可得：$\begin{cases}x'=xcosθ-ysinθ\\\\y'=ycosθ+xsinθ\end{cases}$
  写成旋转矩阵为：

  $$ \begin{pmatrix} x' \\\ y' \\\z' \end{pmatrix} = \begin{pmatrix} cosθ & -sinθ & 0 \\\ sinθ & cosθ & 0 \\\ 0 & 0 & 1 \\\ \end{pmatrix} \begin{pmatrix} x \\\ y \\\z \end{pmatrix} $$

任意三维旋转

渲染

• 给三维物体拍照片
• 1. 摆好模型 Model transformation
  2. 摆好照相机 View transformation
  3. 投影到相片 Projection transformation

View Transformation

• 通过旋转和平移，把世界坐标系中的相机调整到标准姿态

• 相机的姿态包括：位置、朝向和旋转

  标准姿态：

  1. 光心在原点；
  2. 朝着-z方向看；
  3. 向上是y轴

• 从标准姿态变换到当前姿态，再取逆，就是视图变换

正交投影

• 平行光
• 把空间中的长方体映射到一个边长为2的立方体（左右下上远近的边界都是1）
  1. 中心平移到原点: $\begin{pmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\\\ 0 & 1 & 0 & -\frac{t+b}{2} \\\\ 0 & 0 & 1 & -\frac{n+f}{2} \\\\ 0 & 0 & 0 & 1 \end{pmatrix}$
  2. 缩放到2: $\begin{pmatrix}\frac{2}{r-l} & 0 & 0 & 0 \\\\ 0 & \frac{2}{t-b} & 0 & 0 \\\\ 0 & 0 & \frac{2}{n-f} & 0 \\\\ 0 & 0 & 0 & 1\end{pmatrix}$

透视投影

• 视锥
• 近大远小
• 把棱台挤压成长方体，长方体再做正交投影

  1. 远平面缩放到与近平面相同大小

     根据相似，确定不同深度的缩放系数

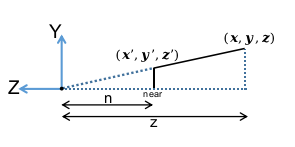     $$ \begin{cases} y'=\frac{n}{z}y \\\ x'=\frac{n}{z}x \\\ z'=unknow \end{cases} $$

     远平面缩放之后各点坐标：

     $$ \begin{pmatrix} \frac{nx}{z} \\\ \frac{ny}{z} \\\ unknown \\\ 1 \end{pmatrix} \overset{乘以深度z}{==} \begin{pmatrix} nx \\\ ny \\\ unkown \\\ z \end{pmatrix} $$

  2. 确定$M\_{persp→ortho}$

     $$ M\_{persp→ortho}^{(4×4)} \begin{pmatrix} x \\\ y \\\ z \\\ 1 \end{pmatrix}= \begin{pmatrix} nx \\\ ny \\\ unknown \\\ z \end{pmatrix} $$$$ M_{persp→ortho}^{(4×4)} = \begin{pmatrix} n & 0 & 0 & 0 \\\ 0 & n & 0 & 0 \\\ ? & ? & ? & ? \\\ 0 & 0 & 1 & 0 \\\ \end{pmatrix} $$

     近平面上的点作用之后不变：

     $$ \begin{pmatrix} n & 0 & 0 & 0 \\\ 0 & n & 0 & 0 \\\ ? & ? & ? & ? \\\ 0 & 0 & 1 & 0 \\\ \end{pmatrix} \begin{pmatrix} x \\\ y \\\ n \\\ 1 \end{pmatrix} = \begin{pmatrix} x \\\ y \\\ n \\\ 1 \end{pmatrix} = \begin{pmatrix} nx \\\ ny \\\ n^2 \\\ n \end{pmatrix} $$

     因为$n^2$与x,y无关，所以第三行为：(0 0 A B), $An+B=n^2$

     远平面的中心点也没变，满足：

     $$ \begin{pmatrix} n & 0 & 0 & 0 \\\ 0 & n & 0 & 0 \\\ 0 & 0 & A & B \\\ 0 & 0 & 1 & 0 \\\ \end{pmatrix} \begin{pmatrix} 0 \\\ 0 \\\ f \\\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\\ 0 \\\ f \\\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\\ 0 \\\ f^2 \\\ f \end{pmatrix} $$

     所以$Af+B=f^2$

     联立可解得A,B:

     $$ \begin{cases} An+B=n^2 \\\ Af+B=f^2 \end{cases} ⇒ \begin{cases} A=n+f \\\ B=-nf \end{cases} $$

  3. 透视投影矩阵：$M_{persp} = M_{ortho} M_{persp→ortho}$