Table of contents
Note
GL_PROJECTION matrix:
camera space point(xe,ye,-ze) -> perspective projection to near plane -> homo:(xp,yp,1) -> scale -> homo:(xn,yn,zn,1) -> (x_clip,y_clip,z_clip, w_clip)
, where ‘xn,yn,zn’ are variables raning from -1 to 1.
Refer to OpenGL Projection Matrix - songho
Normalized Device Coordinates (NDC) is used to determine whether a 3D point can appear on the computer monitor, which is a cube with length 1. The transformation from eye coordinates to NDC is mapping the truncated pyramid frustum to a cube.
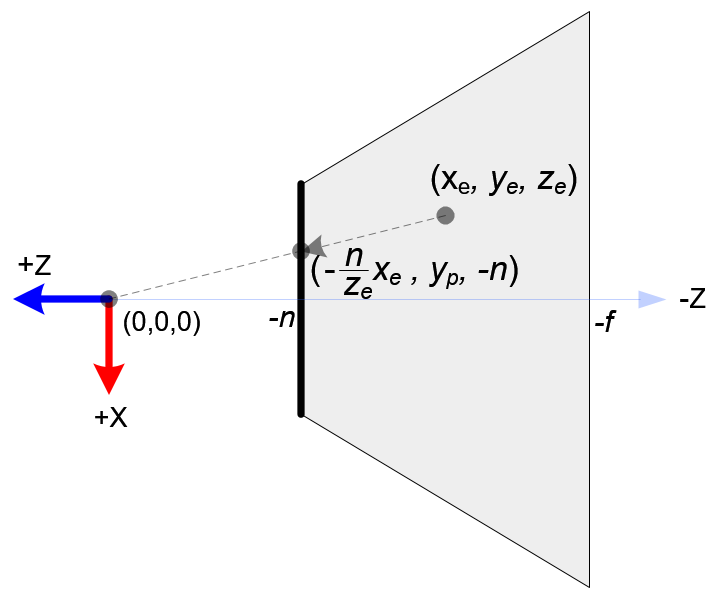
Perspective Projection - songho
According to the perspective projection, the projection point of a world point (xₑ,yₑ,zₑ) on the near plane is
$$ \begin{cases} x_p = \frac{n}{-z_e} x_e \\\ y_p = \frac{n}{-z_e} y_e \end{cases} $$(Camera coordinates is right-hand system looking in the -z direction, while NDC is looking in the z direction under left-hand coordinates)
In order to use a matrix to represent NDC transformation, the homogeneous coordinates are used to enable division, so the transformation can be represented as:
$$ \begin{pmatrix} x_{clip} \\\ y_{clip} \\\ z_{clip} \\\ w_{clip} \end{pmatrix} = M_{projection} \cdot \begin{pmatrix} x_e \\\ y_e \\\ z_e \\\ w_e \end{pmatrix} $$-
(2024-02-15) wₑ is the homogeneous coordinate for storing the original depth value of the camera point after the multiplication with the projection matrix, where the 4-th row is [0 0 -1 0], so wₑ = 1. And the depth will be divided at the very end step: the perspective division, so as to make the intermediate processes linear operations.
Comparing merely projecting a 3D point onto plane with a
w2c, the projection matrix specifies specific behavior for the z-axis of the ND space (not the source camera space any more).
Therefore, the NDC is:
$$ \begin{pmatrix} x_{ndc} \\\ y_{ndc} \\\ z_{ndc} \end{pmatrix} = \begin{pmatrix} x_{clip} / w_{clip} \\\ y_{clip}/w_{clip} \\\ z_{clip}/w_{clip} \end{pmatrix} $$Because $w_{clip}$ is the denominator, it should equal to -zₑ; Hence, the forth row of matrix should be $[0\ 0\ -1\ 0]$
Mapping [l, r] and [b, t] to [-1, 1] with linear realtionship: Two points (l,-1),(r,1) can be used to determine the line:
$$ x_{NDC} = \frac{1-(-1)}{r-l} \cdot x_p + β $$and then substitute (r,1) for $(x_p,x_{NDC})$ to solve β = -(r+l)/(r-l).
Therefore, $x_{NDC} = \frac{2}{r-l}x_p - \frac{r+l}{r-l}$.
Similarly, $y_{NDC} = \frac{2}{t-b} y_p- \frac{t+b}{t-b}$
Substitute xp, yp with the form of xₑ, yₑ:
$$ x_{NDC} = (\frac{2n}{r-l} \cdot x_e + \frac{r+l}{r-l} \cdot z_e) / -z_e \\\ y_{NDC} = (\frac{2n}{t-b} \cdot y_e + \frac{t+b}{t-b} \cdot z_e) / -z_e $$Therefore, the first two row elements of the matrix can be determined.
Suppose the third row is $[0\ 0\ A\ B]$ (z value is independent to x and y), so:
$$ z_{NDC} = \frac{A z_e + B w_e}{-z_e} $$Substitute the correspondence between (-n, -f) and (-1, 1) into the above equation:
$$ \begin{cases} \frac{-A n + B}{n} = -1 \newline \frac{-A f + B}{f} = 1 \end{cases} $$Therefore, A = -(f+n)/(f-n), and B = -2fn / (f-n)
Finally, the matrix $M_{projection}$ is
$$ \begin{pmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\\ 0 & 0 & \frac{-(f+n)}{f-n} & \frac{-2fn}{f-n} \\\ 0 & 0 & -1 & 0 \end{pmatrix} $$Songho’s Idea
References:
-
kaolin.render.camera.PinholeIntrinsics — NVIDIA Kaolin Library documentation
- Mentioned in QQ chat by “Ligo、” at 1:48 AM, Dec 24, 2024
Notes:
(2024-11-30)
-
Songho’s derivation starts with the film coordinates. Specifically, x on the camera film rangers $[l, r]$.
He first scaled the film Coordinates to $[-1, 1]$, obtaining the final ND coordinates.
However, the Projection matrix should transform the camera-space coordinates to the clipping-space coordinates.
So, he substituted the camera-space Coordinates that have performed perspective division, and multiplied the
zvalues with the obtained ND coordinates to get clippling-space coordinates.Finally, he identified the coefficients in the matrix according to the corresponding items.
-
In my opinion, I believe the derivation of Projection matrix could be logical by splitting the transformation into 2 steps: perspective projection and range scaling.
In other words, regarding the Projection Matrix as a product of 2 matrix: intrinsics matrix and a scaling matrix.
Anyway, the main idea for Projection Matrix (or even any projection operation) is range scaling. Specifically, Projection Matrix is used in the process of scaling the camera coordinates to [-1, 1].
-
Illustration of scaling the x range on the camera film to [-1, 1]:
(2024-12-29)
-
Kaolin r1-Docs applies the similar derivation by decomposing the ProjectMatrix to 3 steps:
$\rm FullProjectionMatrix = Ortho \times Depth Scale \times Perspective$
Code
(2023-10-02)
- 3D world coords multiplied with Inverse intrinsics matrix,
- Scale the [near, far] to [0,1]
Code credits MatchNeRF
|
|
near-far = [0,1]
(2024-01-16)