Video 13 Neural Network 2021-11-10
Outline:
- Stochastic gradient descent
- Neural network model
- Backpropagation algorithm
Gradient Descent
-
沿着误差函数 $\mathbf e$ 的负梯度方向,一步一步最小化 in-sample error。
-
Ein 是(线性/非线性)模型的权重 $\mathbf w$ 的函数:
$$ E_{in}(\mathbf w) = \frac{1}{N} \sum_{n=1}^N \mathbf e(h(\mathbf x_n), y_n) $$
$\mathbf e$ 是误差函数,计算假设值与样本真实值之间的误差。复杂的误差函数越难优化。有时不能向 linear regression 那样 one-shot 求出最佳w。可以用梯度下降,一步一步地使误差下降。移动的方向是负梯度方向$-\nabla$,每次移动的大小与 $-\nabla E_{in}$ (Gradient error) 成比例($\eta$是学习率):
$$ \Delta \mathbf w = - \eta \nabla E_{in}(\mathbf w) $$
这里$\nabla$ Ein 是基于所有的样本点($\mathbf x_n, y_n$),叫做"batch GD",也就是使用所有点做了一次梯度下降。
Stochastic gradient descent
-
一次随机选一个点做梯度下降。
Pick one ($\mathbf x_n, y_n$) at a time. Apply GD to $\mathbf e(h(\mathbf x_n),y_n)$
-
N 次梯度下降的“平均方向”(Average direction)还是等于$-\nabla E_{in}$:
$$ \mathbb E_n [-\nabla \mathbf e(h(\mathbf x_n), y_n)] = \frac{1}{N} \sum_{n=1}^N -\nabla \mathbf e(h(\mathbf x_n),y_{n}) = -\nabla E_{in} $$
随机梯度下降是梯度下降的 randomized version
-
SGD 的好处:
- 简化计算 (Cheaper computation): 每次只看一个样本点
- 随机化 (Randomization): 避免陷入局部最小或鞍点,无法继续优化。如果使用“batch GD”,那么初始位置最关键,因为只走一步,所以容易陷入附近的局部最优。
- 简单 (Simple)
-
Rule of thumb (经验法则): $\eta = 0.1$ works
-
例子:电影评分
User $u_i$ 的喜好有K个属性,Movie $v_j$ 的也有对应的K个属性。根据这个用户他之前评价过的电影 $r_{ij}$ (rating),调整用户的各属性权重,最小化误差。
$$ \mathbf e_{ij} = \left( \underbrace{ r_{ij}}{\text{actual}} - \underbrace{\sum{k=1}^K u_{ik}v_{jk}}_{\text{predict}} \right)^2 $$
反过来,把用户属性输入模型就可以估计某电影的评分
…
2D perceptron 的break point=4,也就是感知机无法解决异或问题。
…
Neural Network model
-
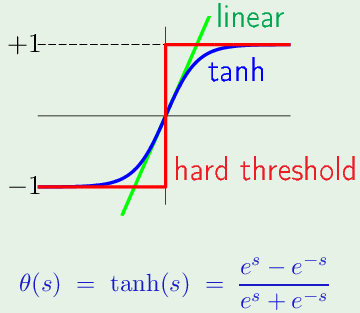
对于从神经元 $i$ 出发,指向第 $l$ 层的神经元 $j$ 的权重 $w_{ij}^{(l)}$
$$ \begin{cases} 1 \leq l \leq L & \text{隐藏层/输出层序号, 输入层是0} \ 0 \leq i \leq d^{(l-1)} & \text{w出发的神经元: 0代表从bias出发}\ 1 \leq j \leq d^{(l)} & \text{w指向的神经元: 至少有一个,最多有$d^{l}$}\ \end{cases} $$
第 $l$ 层的某神经元,接受了来自上一层所有神经元的输入(内积):
$$ x_j^{(l)} = \theta(s_j^{(l)}) = \theta \left( \sum_{i=0}^{d^{(l-1)}} w_{ij}^{(l)} x_i^{(l-1)} \right) $$
从bias term 开始加到第 $d^{(l-1)}$ 个,把信号 $s_j^{(i)}$ 传入 $\theta$ 非线性激活函数
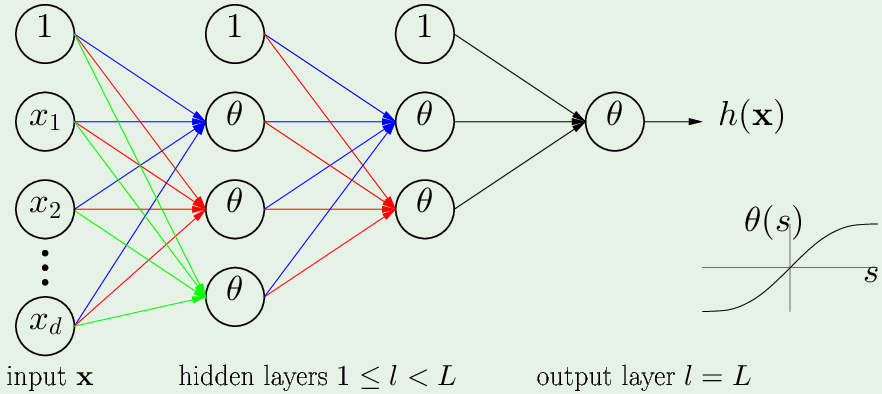
一个样本 $\mathbf x$ 有$d^{(0)}$ 个维度,所以输入层对应有:$x_1^{(0)} \cdots x_{d^{(0)}}^{(0)}$,经过一层一层传递,直到最终输出一个值:$x_1^{(L)} = h(\mathbf x)$
Backpropagation algorithm
-
应用随机梯度下降,调节神经网络的权重,使误差函数最小
-
网络全部的权重 $\mathbf w = {w_{ij}^{(l)}}$ 决定了一个假设 $h(\mathbf x)$ (输入到输出的映射)
对于一个样本 $(\mathbf x_n,\ y_n)$ 上的误差:$\mathbf e(h(\mathbf X_n),\ y_n) = \mathbf e(\mathbf w)$,使用SGD,调整权重,减小误差
-
误差函数对每个权重求梯度:
$$ \nabla \mathbf e(\mathbf w): \frac{\partial \mathbf e(\mathbf w)}{\partial w_{ij}^{(l)}}, \quad \text{for all } i,j,l $$
-
计算误差函数 $\mathbf e$ 对各权重 w 的梯度 $\frac{\partial \mathbf e(\mathbf w)}{\partial w_{ij}^{(l)}}$
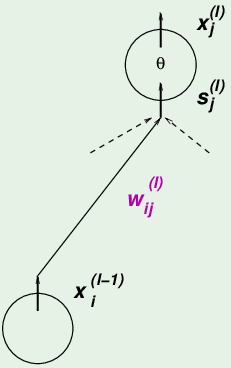
误差 $\mathbf e$ 是实际输出 $\theta(s)$ 减去真实值 $y$,所以误差函数首先是 $s_{j}^{(l)}$ 的函数,第 $l$ 层的第 $j$ 个神经元的输入信号$s_{j}^{(l)}$ 是来自上一层所有神经元的输出贡献之和,所以 $s_{j}^{(l)}$ 是 $w_{ij}^{(l)}$ 的函数,根据链式求导法则:
$$ \frac{\partial \mathbf e(\mathbf w)}{\partial w_{ij}^{(l)}} = \frac{\partial \mathbf e(\mathbf w)}{\partial s_{j}^{(l)}} \times \frac{\partial s_{j}^{(l)}}{\partial w_{ij}^{(l)}} $$
其中:$\frac{\partial s_{j}^{(l)}}{\partial w_{ij}^{(l)}} = x_i^{(l-1)}$,也就是前一层的神经元的输出。 把误差对输入信号的导数称为:$\delta_j^{(l)} = \frac{\partial \mathbf e(\mathbf w)}{\partial s_{j}^{(l)}}$。
所以(某神经元上的)误差对各权重 w 的梯度等于:$\frac{\partial \mathbf e(\mathbf w)}{\partial w_{ij}^{(l)}}= \delta_j^{(l)} x_i^{(l-1)}$。
计算$\delta$:
从最后一层(输出层$l=L,\ j=1$)的 $\delta_1^{(L)}$ 开始计算,输出神经元的输入信号是 $s_1^{(L)}$:
$$ \begin{aligned} \delta_1^{(L)} &= \frac{\partial \mathbf e(\mathbf w)}{\partial s_1^{(L)}}\ \mathbf e(\mathbf w) &= \left ( x_1^{(L)}- y_n \right)^2 & \text{预测值-实际值} \ x_1^{(L)} &= \theta(s_1^{(L)}) & \text{神经元的输出是$\theta$的输出} \ \theta’(s) &= 1 - \theta^2(s) & \text{for the tanh} \end{aligned} $$
之前层 ($l-1$层) 神经元上的误差对其输入信号的导数:
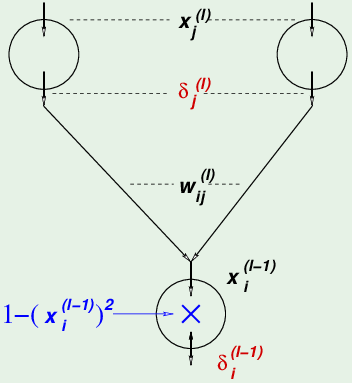
因为第 $l-1$ 层的某个神经元会对第 $l$ 层的全部神经元都有贡献,所以它的误差来自第 $l$ 层的全部神经元 $\delta_j^{(l)}$,所以需要求和。根据链式法则,误差$\mathbf e$ 从上一层 ($l$层) 过来,所以首先是 $s^{(l)}$ 的函数,然后$s^{(l)}$ 是第 $(l-1)$ 层神经元 $x^{(l-1)}$ 的函数,最后 $x^{(l-1)}$ 才是它输入信号 $s^{(l-1)}$ 的函数:
$$ \begin{aligned} \delta_i^{(l-1)} &= \frac{\partial \mathbf e(\mathbf w)}{\partial s_i^{(l-1)}} \ &=\sum_{j=1}^{d^{(l)}} \frac{\partial \mathbf{e}(\mathbf{w})}{\partial s_{j}^{(l)}} \times \frac{\partial s_{j}^{(l)}}{\partial x_{i}^{(l-1)}} \times \frac{\partial x_{i}^{(l-1)}}{\partial s_{i}^{(l-1)}} & \text{第$l$层所有神经元误差求和}\
&=\sum_{j=1}^{d^{(l)}} \delta_{j}^{(l)} \times w_{i j}^{(l)} \times \theta^{\prime}\left(s_{i}^{(l-1)}\right) \
\delta_{i}^{(l-1)} &=\left(1-\left(x_{i}^{(l-1)}\right)^{2}\right) \sum_{j=1}^{d^{(l)}} w_{i j}^{(l)} \delta_j^{(l)} & \text{$\theta$与j无关,求导放前面; $x_i^{l-1}$也就是$\theta(s)$} \end{aligned} $$
所以最后一层之前层的神经元的 $\delta$ 等于 1 减去这个神经元输出的平方,再乘上从它出发的各权重与下一层的$\delta$ 的内积之和。最后一层的$\delta^{(L)}$算出来了,才能算倒数第2层的$\delta^{(L-1)}$,从而可以反向地一层一层求出误差$\mathbf e$ 对各个权重 w 的梯度。
-
Backpropagation algorithm:
- Initialize all weights $w_{ij}^{(l)}$ at random
- for t=0,1,2, …, do //循环
- Pick $n \in { 1,2,\cdots,N }$ //从N个样本中挑一个
- Forward: Compute all $x_j^{(l)}$ //计算每个神经元的输出,从而得出预测值
- Backward: Compute all $\delta_j^{l}$ //计算每个神经元的误差(贡献)
- Update the weights: $w_{ij}^{(i)} \leftarrow w_{ij}^{l} - \eta x_i^{(l-1)} \delta_j^{(l)}$ //迭代直到收敛
- Iterate to the next step until it is time to stop
- Return the final weights $w_{ij}^{l}$
Final remark: hidden layers
隐藏层是在“模仿”非线性变换:把高维样本(线性不可分)变换到新的维度空间,叫做“learned nonlinear transform”。隐藏层的每个神经元是 “learned feature”。
神经元数量越多,自由度越多(有效参数越多),VC维越高,模型复杂度越高,需要更多的样本,才能保证可以从 $E_{in}$ 泛化到Eout.
Example:
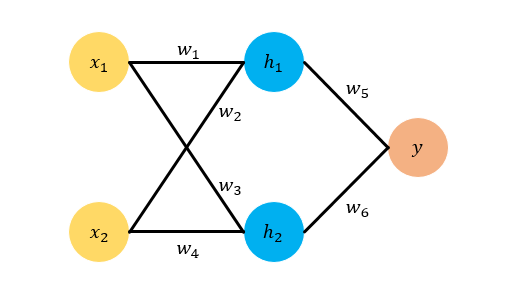
令 $x_1=1, x_2=0.5$ ,然后我们令 $w_1, w_2, w_3, w_4$ 的真实值分别是 1,2,3,4 ,令 $w_5, w_6$ 的真实值是 $0.5, 0.6$ 。这样我们可以算出 $y$ 的真实目标值是 $t=4$ 。
那么为了模拟一个Back Propagation的过程,我们假设我们只知道 $x_1=1, x_2=0.5$ ,以及对应的目标 $t=4$ 。我们不知道 $w_1,w_2,w_3,w_4,w_5,w_6$ 的真实值,现在我们需要随机为他们初始化值,假设我们的随机化结果是 $w_1=0.5, w_2=1.5, w_3=2.3, w_4=3, w_5=1, w_6=1$。
-
Forward: 计算 $h_1, h_2, y$ 的预测值和误差项 E,其中 $E=\frac{1}{2}(t-y)^2$
$$ \begin{aligned} h_1 &= w_1 \cdot x_1 + w_2 \cdot x_2 = 0.5 \cdot 1 + 1.5 \cdot 0.5 = 1.25 \ h_2 &= w_3 \cdot x_1 + w_4 \cdot x_2 = 2.3 \cdot 1 + 3 \cdot 0.5 = 3.8 \ y &= w_5 \cdot h_1 + w_6 \cdot h_2 = 1 \cdot 1.25 + 1 \cdot 3.8 = 5.05 \ E &= \frac{1}{2} (y-t)^2 = 0.55125 \end{aligned} $$
-
Backward
updata $w_5$:
$$ \begin{aligned} \frac{\partial E}{\partial w_5} &= \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial w_5} = (y-t)\cdot h_1 = 1.05 \cdot 1.25 =1.3125 \
\frac{\partial E}{\partial y} &= (t-y)\cdot -1 = y-t \ \frac{\partial y}{\partial w_5} &= \frac{\partial (w_5 h_1 + w_6 h_2)}{\partial w_5} = h_1 \ w_5^+ &= w_5 - \eta \cdot \frac{\partial E}{\partial w_5} = 1-0.1\cdot 1.3125 = 0.86875 \end{aligned} $$
updata $w_6$:
$$ \begin{aligned} \frac{\partial E}{\partial w_6} &= \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial w_6} = (y-t)\cdot h_2 = 1.05 \cdot 3.8 = 3.99 \ w_6^+ &= w_6 -\eta \cdot \frac{\partial E}{\partial w_6} = 1-0.1\cdot 3.99 = 0.601 \end{aligned} $$
下面我们再来看 $w_1, w_2, w_3, w_4$ ,由于这四个参数在同一层,所以求梯度的方法是相同的
updata $w_1$:
$$ \begin{aligned} \frac{\partial E}{\partial w_1} &= \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial h_1} \cdot \frac{\partial h_1}{\partial w_1} = (y-t) \cdot w_5 \cdot x_1 = 1.05 \cdot 1 \cdot 1 = 1.05 \
w_1^+ &= w_1 - \eta \cdot \frac{\partial E}{\partial w_1} = 0.5 - 0.1 \cdot 1.05 = 0 .395 \end{aligned} $$
updata $w_2$:
$$ \begin{aligned} \frac{\partial E}{\partial w_2} &= \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial h_1} \cdot \frac{\partial h_1}{\partial w_2} = (y-t) \cdot w_5 \cdot x_2 = 1.05 \cdot 1 \cdot 0.5 = 0.525 \
w_2^+ &= w_2 - \eta \cdot \frac{\partial E}{\partial w_2} = 1.5 - 0.1 \cdot 0.525 = 1.4475 \end{aligned} $$
updata $w_3$:
$$ \begin{aligned} \frac{\partial E}{\partial w_3} &= \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial h_2} \cdot \frac{\partial h_2}{\partial w_3} = (y-t) \cdot w_6 \cdot x_1 = 1.05 \cdot 1 \cdot 1 = 1.05 \
w_3^+ &= w_3 - \eta \cdot \frac{\partial E}{\partial w_3} = 2.3 - 0.1 \cdot 1.05 = 2.195 \end{aligned} $$
updata $w_4$:
$$ \begin{aligned} \frac{\partial E}{\partial w_4} &= \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial h_2} \cdot \frac{\partial h_2}{\partial w_4} = (y-t) \cdot w_6 \cdot x_2 = 1.05 \cdot 1 \cdot 0.5 = 0.525 \
w_4^+ &= w_4 - \eta \cdot \frac{\partial E}{\partial w_4} = 3 - 0.1 \cdot 0.525 = 2.9475 \end{aligned} $$
-
Forward:
$$ \begin{aligned} h_1 &= w_1 \cdot x_1 + w_2 \cdot x_2 = 0.395 \cdot 1 + 1.4475 \cdot 0.5 = 1.11875 \ h_2 &= w_3 \cdot x_1 + w_4 \cdot x_2 = 2.195 \cdot 1 + 2.9475 \cdot 0.5 = 3.66875 \ y &= w_5 \cdot h_1 + w_6 \cdot h_2 = 0.97191 + 2.204918 = 3.17683 \ E &= \frac{1}{2} (y-t)^2 = 0.338802 \end{aligned} $$