Source video: 傅立叶变换如何理解？美颜和变声都是什么原理？李永乐老师告诉你

变换

向量可以从图形“变换”成数，也可以从数“逆变换”回图形

向量的图像与数组是一一对应的。向量相加对应数组相加。

向量 A 被表示为 (2,4)，其含义为 A 在 x 方向上有 2 个单位长度 ex，在 y 方向上有 4 个单位长度 ey。

因为：

1. 𝒆x 和 𝒆y 的长度（自己与自己的内积）都等于 1 ： 𝒆x⋅ex = ey⋅ey = 1

2. ex 与 ey 正交（垂直），两者内积等于 0： ex ⋅ ey = |ex|⋅|ey|⋅cos90° = 0

所以 ex 和 ey 是一组标准正交基。 空间中的任何一个向量都可以变成标准正交基的组合。

傅里叶级数

任何一个周期性的函数 f(t) 都可以变换为一系列正余弦函数的和。 正弦余弦函数就是一组正交基。

它的逆变换是显而易见的，因为 sin 和 cos 都是周期性的，它们组合出来的函数也一定是周期性的。

对于一个周期性函数，按照不同频率 w 分解出不同的正余弦函数（波）：

如上图，在频率方向上，一个周期性波可以分解成一个频率为 w 的正弦函数，与一个频率为 2w 的分量（振幅比较大），再与一个频率为 3w 的分量（振幅比较小）相加。

从后方观察，以时间为坐标系，只能看到信号随时间的变化； 从侧面观察，以频率为坐标系，一个信号是多个信号的累加。

因为分量是有限个，所以频谱图上是一条条竖线，不同的高度代表振幅的大小。 不同频率的分量，除了振幅不同，起始点也不同，所以还需要一个轴表示相位：

时域里的信号 f 变换到频域里的三个维度：频率 w，振幅 F(f)，相位 φ。

如果已知频域中的 w, F(f), φ，就可以把它们组合起来，逆变换到时域中的信号。

$$ f(t) = \frac{a_0}{2} + \sum_i a_n sin(n w t + φ_n) \\ \quad = \frac{a_0}{2} + \sum_i a_n sin(n w t) + \sum_i b_n cos(n w t) $$

n 是整数，nw 是不同的频率，aₙ 是振幅，φₙ 是相位。 按照第2行的写法，标准正交基有 3 个：1， sin(nwt), cos(nwt)

任何一个周期性的函数都可以分解成以上 3 个标准正交基的线性组合。 （sin(nwt) 与 cos(nwt) 是一对，拆不开？）

连续傅里叶变换

非周期信号可以看作是周期无穷大的周期性信号。

欧拉公式

用一个平面坐标系表示虚数，则横轴表示实部，纵轴表示虚部。 横轴的单位为1，纵轴的单位为虚数单位 i，则单位圆上任何一点 A 可以表示为： cosθ + i⋅sinθ。

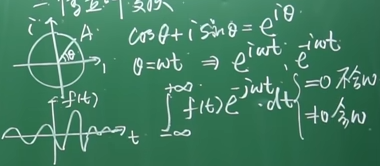
令 θ = wt，w 取不同的频率，对应 A 点在圆上逆时针转动不同的角度

根据欧拉公式：

$$ cosθ + i⋅sinθ = e^{iθ} \\ cos(wt) + i⋅sin(wt) = e^{iwt} $$

所以 A 在逆时针旋转时，每时每刻都代表了两个正交基 cosθ, sinθ。 如果是 $e^{-iwt}$ 就是顺时针旋转。

FT: 用正交基"摘"分量

一个非周期性的时域信号肯定也包含各种频率的信号分量， 又因为标准正交基与自己的内积为 1，与其他正交基的内积为 0， 所以可以用各个正交基与该信号内积，则留下的就只是在这个基向量上的分量。

非周期性时域信号的频率分量有无穷个，所以傅里叶变换是用积分：

$$ \^F_T(w) = ∫_{-∞}^{+∞} f(t) e^{-jwt} dt \\ \ \\ f(t) e^{-jwt} \begin{cases} =0 & \text{f(t) 不含 sin(wt),cos(wt)} \\ \neq 0 & \text{f(t) 含有 sin(wt),cos(wt)} \end{cases} $$

其中 $e^{-jwt}$ 是一组正交基 sin(wt) 和 cos(wt)。

$\^F_T(w)$ 是个复数（带 i），实部表示振幅，虚部是相位，而且是连续的 ，意味着每个频率的正（余）弦函数都有分量，

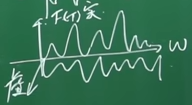
IFT: 正交基加权和

$F_T(w)$ 是各正交基（正弦余弦函数）的”系数“，即在各正交基上的”长度“。

从频域信号逆变换回时域信号，就把系数乘到基向量上，再加起来：

$$ f(t) = ∫_{-∞}^{+∞} F_T(w) e^{-jwt} dw $$

应用

声音信号是时域，横坐标是时间；图像信号是空间域，横坐标是空间位置

低频分量是图像的轮廓，高频分量是细节