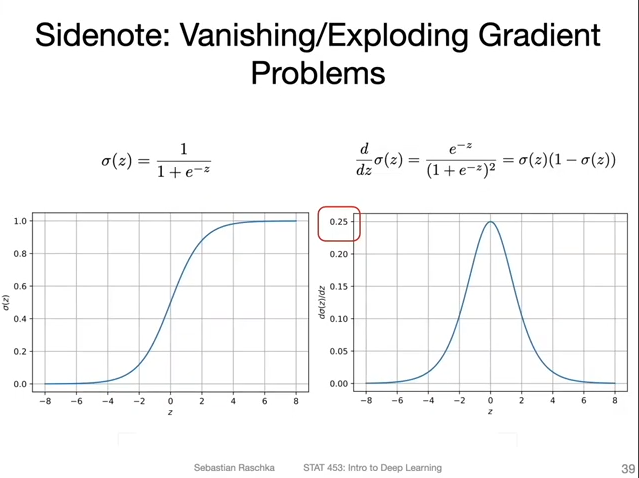
The maximum gradient of the sigmoid activation function is 0.25, which may cause partial derivative of loss with respect to the earlier weight w very small after passing throught multipler layers.
And scaling the weights down can mitigate the gradient decrease.
Based on the chain rule, the derivative of the weight in the fisrt layer (l=1) is ∂loss/∂w¹ = ∂loss/∂o ⋅ ∂o/∂a² ⋅ ∂a²/∂a¹ ⋅ ∂a¹/∂w¹, where a = g(z), g is an activation function.
If the weight w¹ is small, the activation z¹ is small (around zero), so ∂a¹/∂z¹ corresponds to the highest derivative. And also if w² is small, ∂a²/∂a¹ = ∂a²/∂z²⋅ ∂z²/∂a¹, where ∂a²/∂z² will be a big derivative. Hence, ∂loss/∂w¹ can maintain a high derivative.
So it’s importance to initialize the weights centered at zero with small variance for getting the maximum gradient. L11.5 Weight Initialization – Why Do We Care?
Activation z is a sum of wᵢxᵢ, so it may be exploding or vanishing quickly if the W doesn’t have constriant. Weight Initialization in a Deep Network (C2W1L11) - Andrew Ng
Xavier (Glorot) initialization
L11.6 Xavier Glorot and Kaiming He Initialization - Sebastian Raschka
- Step 1: Initialize weights from Gaussian or uniform distribution
- Step 2: Scale the weights proportional to the number of input features to the layer
In particular, the weights of layer l is defined as: 𝐖 ⁽ˡ⁾ ≔ 𝐖 ⁽ˡ⁾⋅ √(1/m⁽ˡ⁻¹⁾), where m is the number of input units of the previous layer (𝑙-1) to the next layer (𝑙).
𝐖 is initialized from Gaussion (or uniform) distribution: Wᵢⱼ⁽ˡ⁾~N(μ=0, σ²=0.01)
Rationale behind this scaling factor:
He (Kaiming) initialization
Usage
Three different commonly used initialization techniques. Here are what their variants need to be set to and which activation functions they work best with.
| Initialization | Activation function | Variance (σ²) | Mean |
|---|---|---|---|
| Glorot | Linear; Tanh; Sigmoid; Softmax | σ² = 1/(½⋅(fanᵢₙ+fanₒᵤₜ)) | 0 |
| He | ReLu; Variants of ReLU | σ² = 2/fanᵢₙ | 0 |
| LeCun | SELU | σ² = 1/fanᵢₙ | 0 |