6-如何理解“梯度下降法”？什么是“反向传播”？通过一个视频，一步一步全部搞明白

正向传播

• 输入数据沿着神经网络正向传递
• 输入数据与各个感知机的w和b点乘，将结果代入激活函数，给出判断结果

反向传播

• 把判断结果的偏差传递给各个w和b，根据参数对偏差贡献的大小，成比例的调整
• 未训练好的神经网络的$\mathbf w,b$不准确，导致判断结果有偏差。如果某 $\mathbf w/b$ 对最终的判断结果有重大影响，则该参数对于偏差也是有重大影响的。所以在减小误差的过程中，应优先调整d对偏差有重大影响的参数。

脑补过程：

神经网络输出层的输出值是 $a^{[3]}$:

$$ \mathbf a^{[3]} = \sigma(\mathbf w^{[3]} \cdot \mathbf a^{[2]} + b^{[3]}) $$

其中 $\sigma$ 是激活函数，$\mathbf w^{[3]}$输出层权重，$\mathbf a^{[2]}$上一层的输出值，$b^{[3]}$是输出层偏置系数。

可以计算损失函数（交叉熵），得到偏差J：

$$ J = \frac{1}{n} \left( -∑_{i=1}^n (y^{(i)}) ⋅ log_2 a^{[3](i)} + (1-y^{(i)} ⋅ log_2(1-a^{[3](i)}) )\right) $$

其中 $y_i$ 是理想系统中输出y的概率；$log₂ a^{[3](i)}$是判断结果的信息量。

偏差直接来自输出层的感知机:

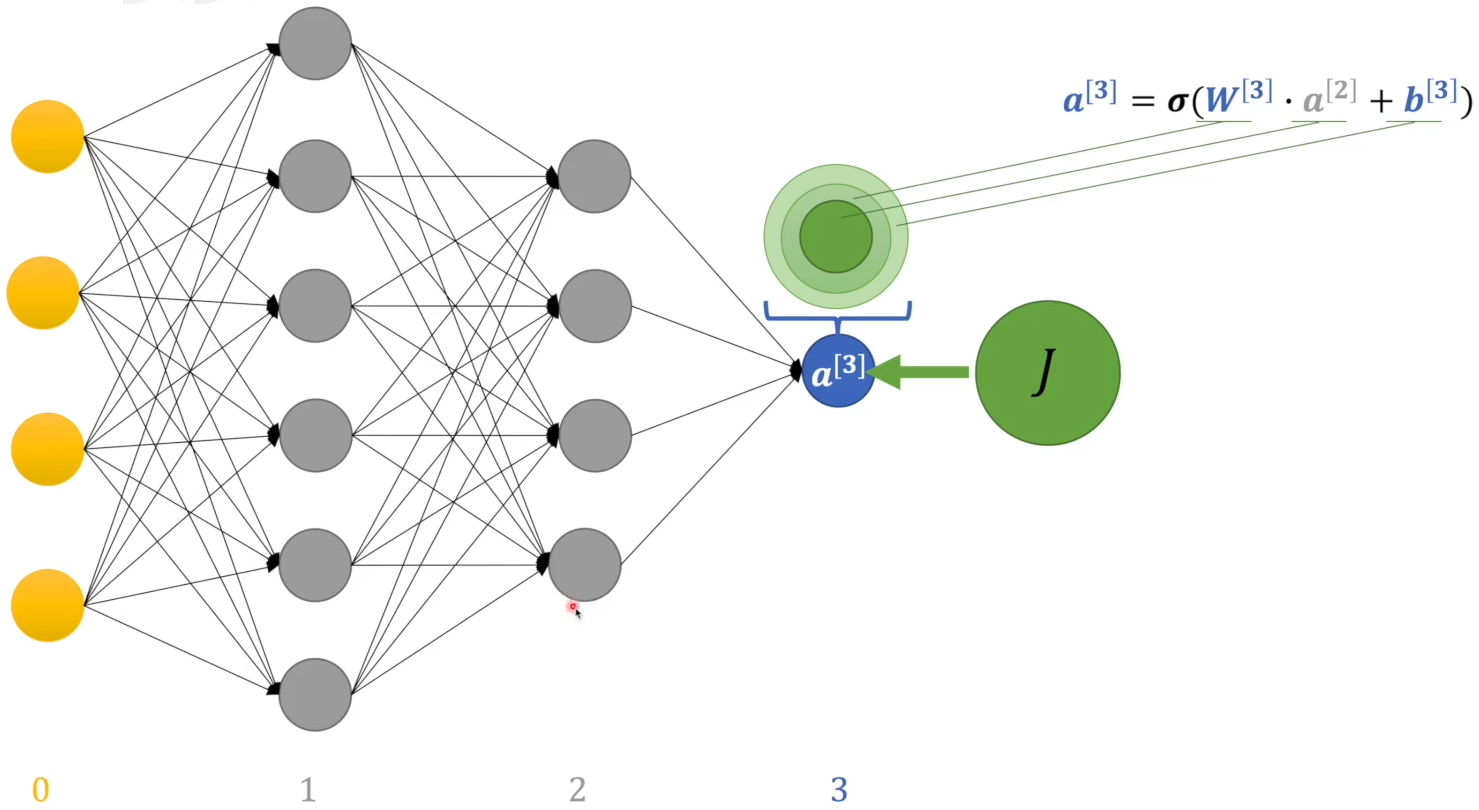
偏差来自三部分：当前层的 w 和 b，以及上一层的输出 $a^{[2]}$。其中 w 和 b 可以根据占比直接调整，而 $a^{[2]}$ 的偏差来自于上一层，按照贡献大小分配偏差：

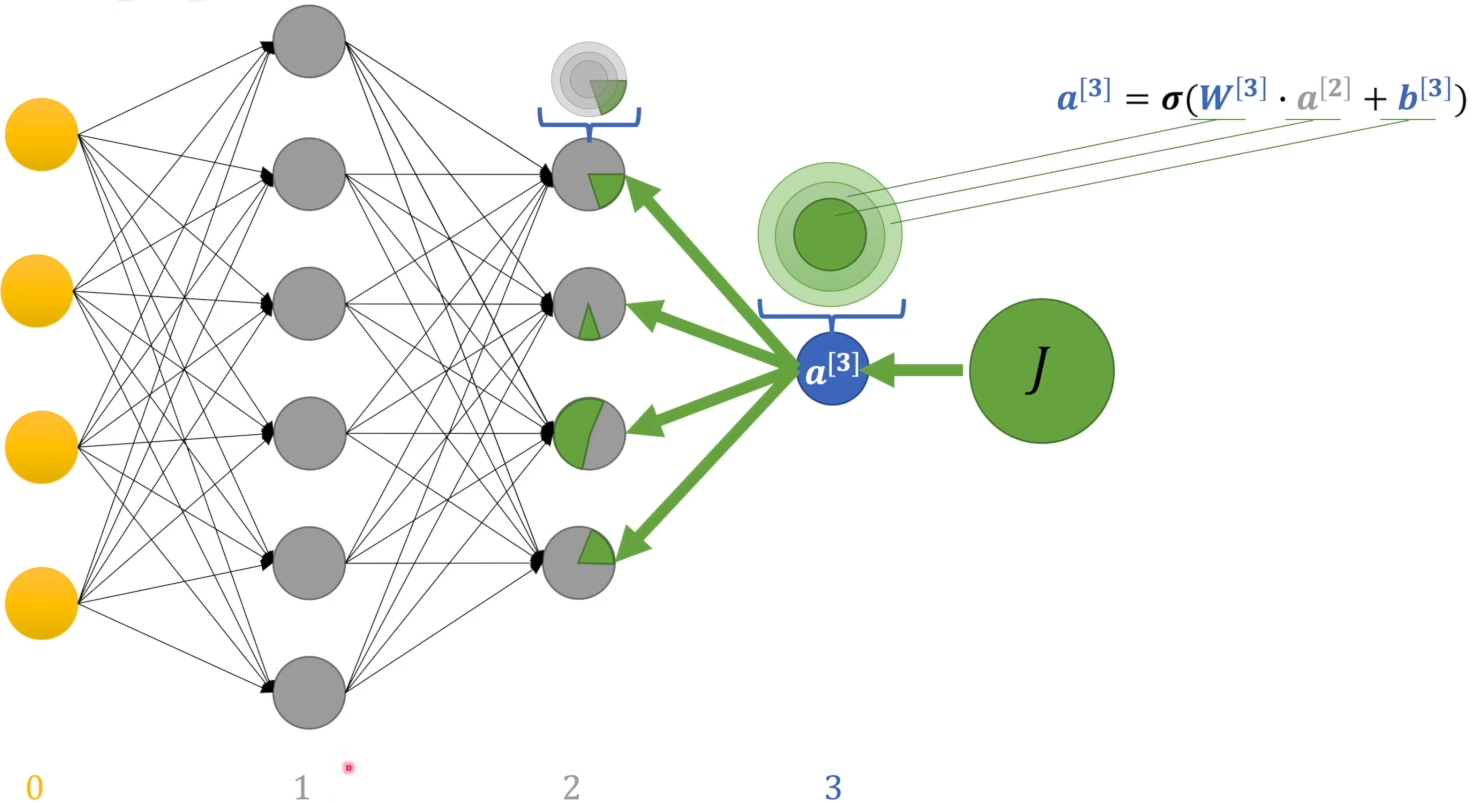
然后前一层的感知机占有的偏差又可分成3部分，调整 $w, b$ 和 上一层的输出.

第一隐藏层的感知机的偏差与第二隐藏层所有感知机相关：

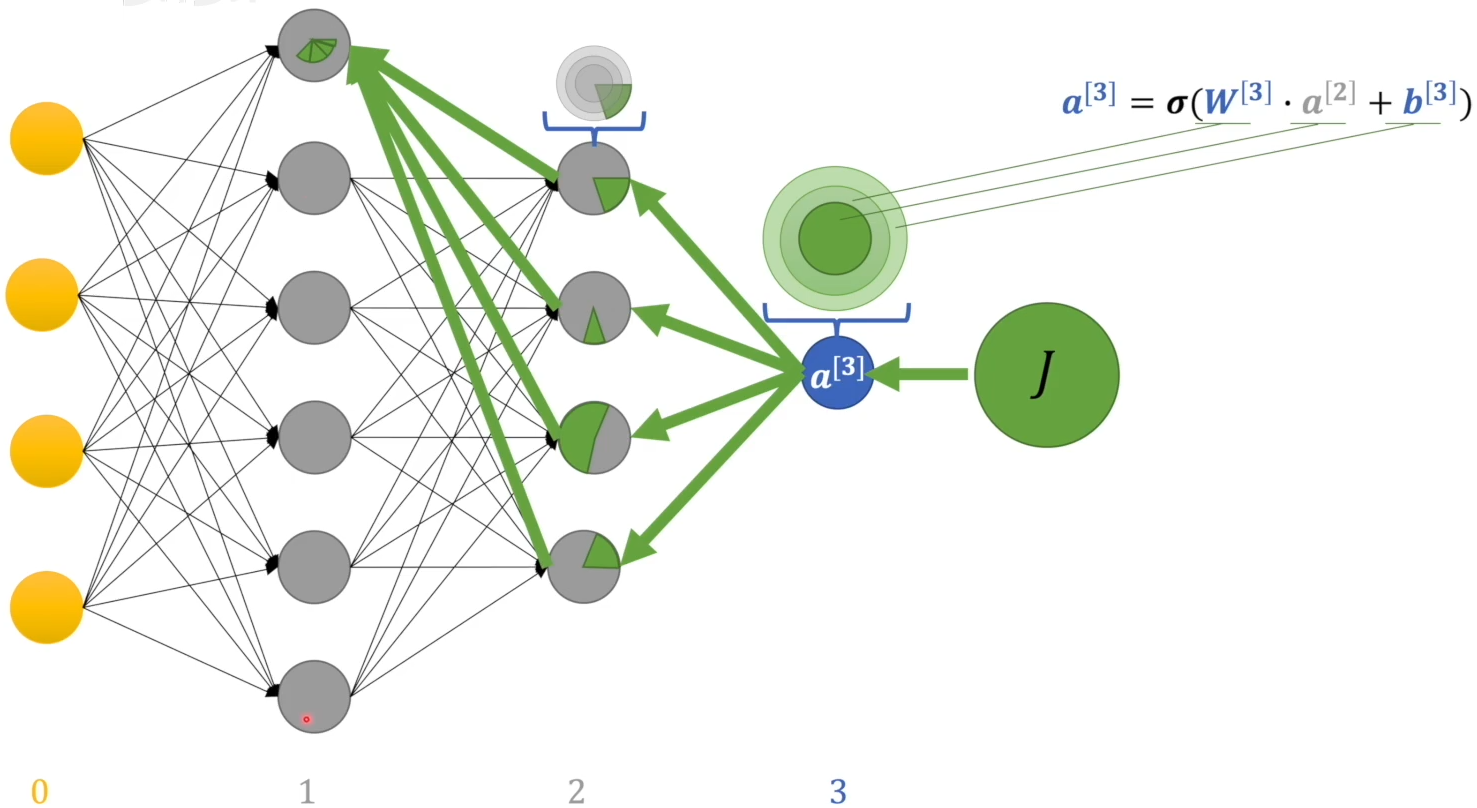
由此，整个神经网络中的每个 $w$ 和 b 都能分配到偏差占比。

以上利用的是数值的加法分配偏差，还可使用向量的加法来分配偏差，不过首先要确定向量的方向。

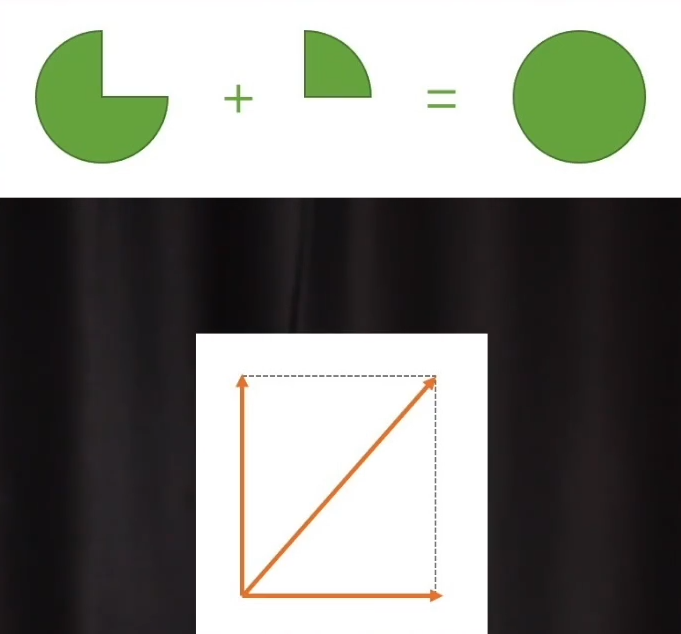
梯度的反方向就是要找的向量方向：数值减小最快的方向。 梯度可以在i方向和j方向上分解，对于点(x,y)沿变化率最大的方向变化就是在i和j方向上同步变化。

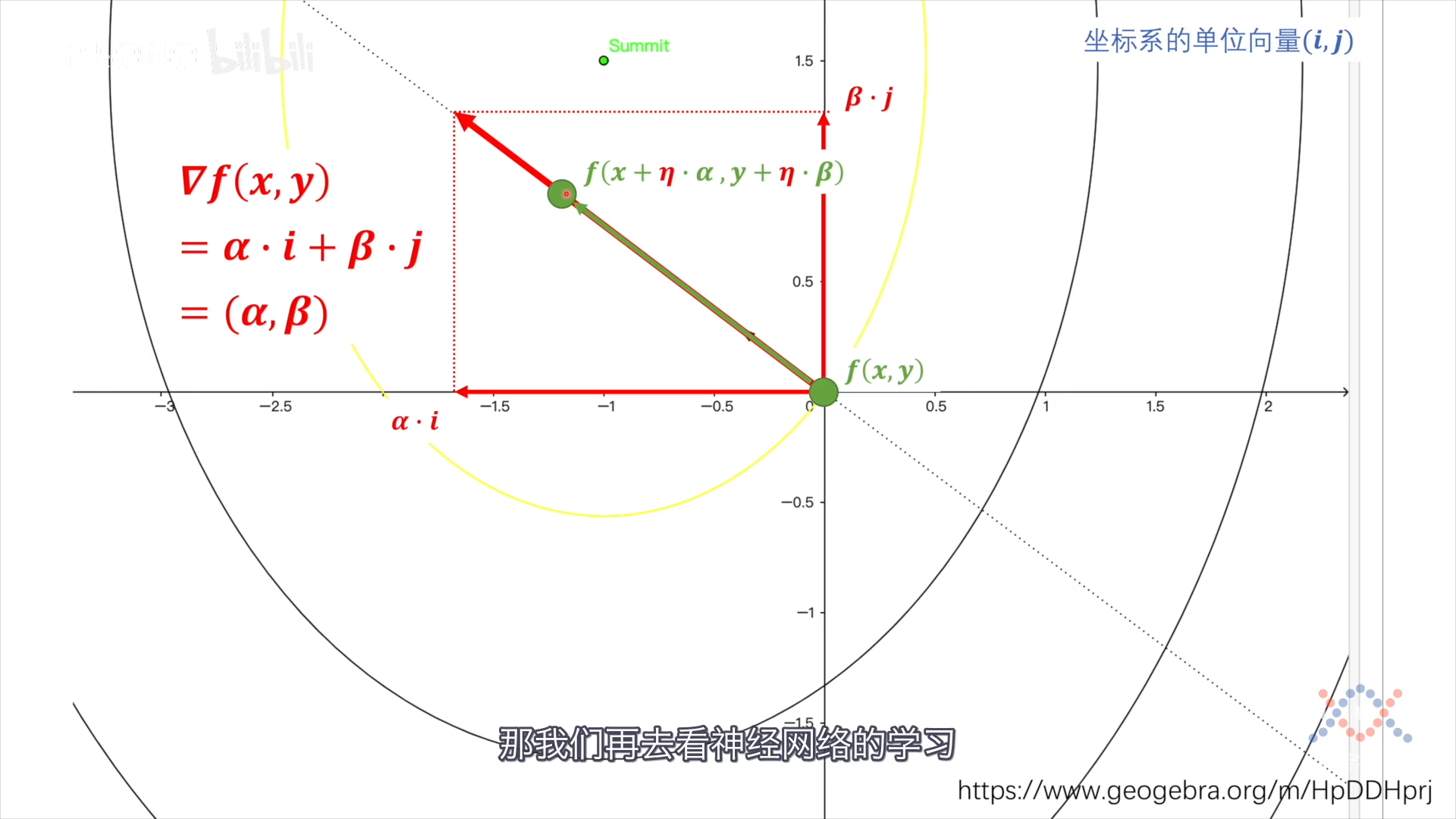
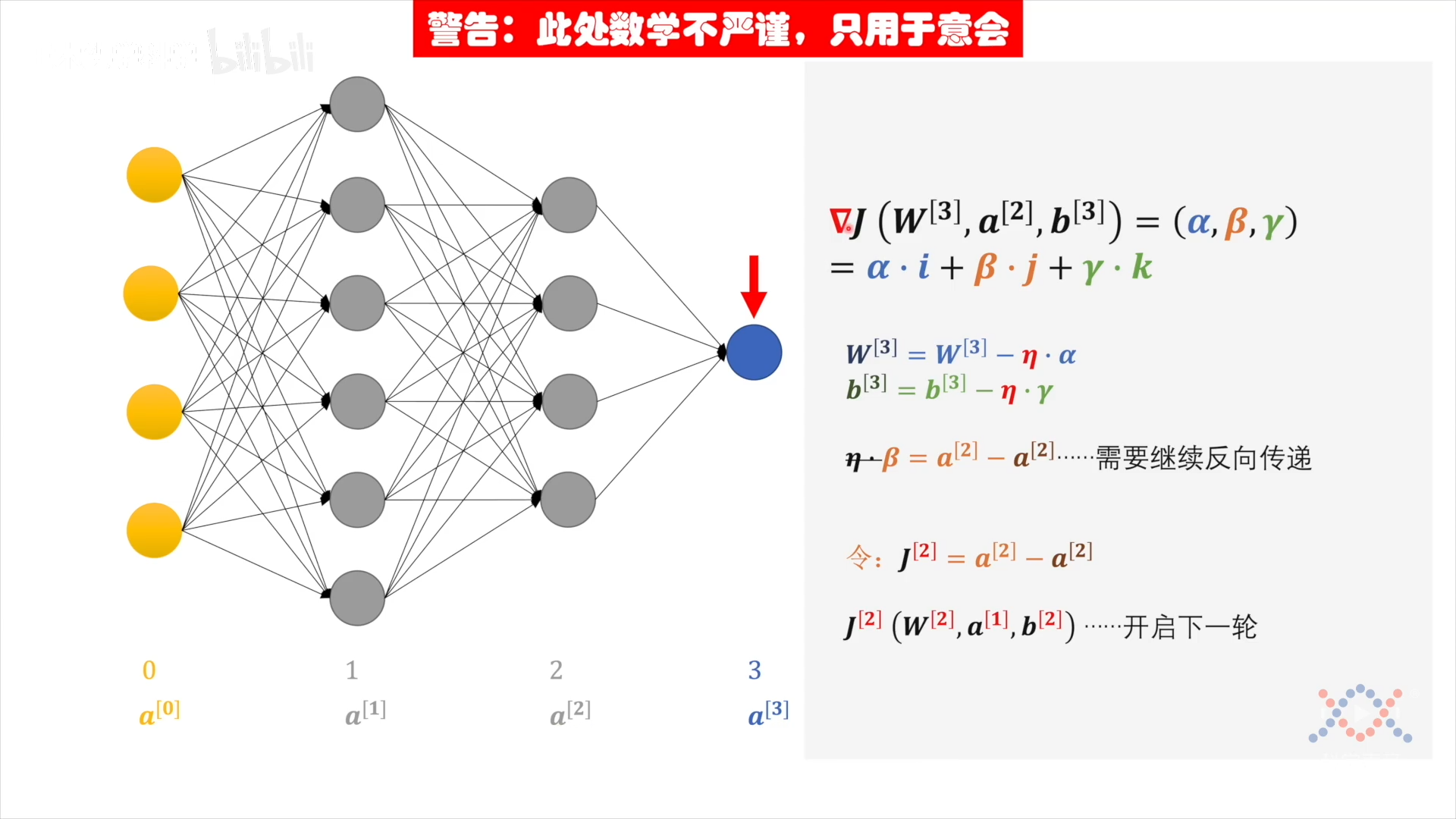
对(输出层)损失函数 J 求梯度：

$$ \begin{aligned} &\nabla J (\mathbf w^{[3]}, a^{[2]}, b^{[3]}) \\ & = (\alpha, \beta, \gamma) & \text{三个分量的系数，简略表示} \\ & = \alpha \cdot \mathbf i + \beta \cdot \mathbf j + \gamma \cdot \mathbf k \end{aligned} $$

输出层的输出沿梯度方向变化$\eta$步长，向目标值靠近：

$$ \begin{aligned} \mathbf w^{[3]}{(\rm target)} &= \mathbf w^{[3]} - \eta \cdot \alpha \ b^{[3]}{(\rm target)} &= b^{[3]} - \eta \cdot \gamma \ \ a^{[2]}{(\rm target)} &= a^{[2]} - \eta \cdot \beta & 需要反向传递分配到第2隐藏层上 \ \cancel{\eta \cdot}\ \beta &= a^{[2]}{(\rm target)} - a^{[2]}_{(\rm now)} \end{aligned} $$

感知机输出值a的中间传递不考虑 $\eta$，偏差最终分配在输入层的w和b上，其中含有$\eta$。从而可以看出隐藏层与输出层类似，也是目标与输出之间的差值。因此对于第2隐藏层的"损失函数"： $J^{[2]} = a^{[2]}{(\rm target)} - a^{[2]}{(\rm now)}$，$J^{[2]} (\mathbf w^{[3]}, a^{[2]}, b^{[3]})$ 开启下一轮：求梯度,求损失函数

各层的运算形式相同（损失函数），就可以迭代分配偏差。J沿梯度方向变化就可以最快的减小偏差，因此使用了向量的加法做偏差分配。

梯度

• 求偏导就是求（固定另一个维度）曲线的切线，两个偏导组合就是两条切线组合，两条切线确定了切面。所以对曲面求偏导，就是在求切面
• 把两个切线合成一个向量，就是梯度

$\alpha, \beta,\gamma$ 的具体表示（求偏导）：

$$ \begin{aligned} \alpha &= \frac{\partial J}{\partial \mathbf w^{[3]}} \ \gamma &= \frac{\partial J}{\partial b^{[3]}} \ \beta &= \frac{\partial J}{\partial \mathbf a^{[2]}} \end{aligned} $$

分配偏差：

$$ \begin{aligned} \mathbf w^{[3]} &= \mathbf w^{[3]} - \eta \cdot \frac{\partial J}{\partial \mathbf w^{[3]}} \ b^{[3]} &= b^{[3]} - \eta \cdot \frac{\partial J}{\partial b^{[3]}} \ \frac{\partial J}{\partial \mathbf a^{[2]}} &= a^{[2]}{(\rm target)} - a^{[2]}{(\rm now)} & \text{“新损失函数”} \end{aligned} $$

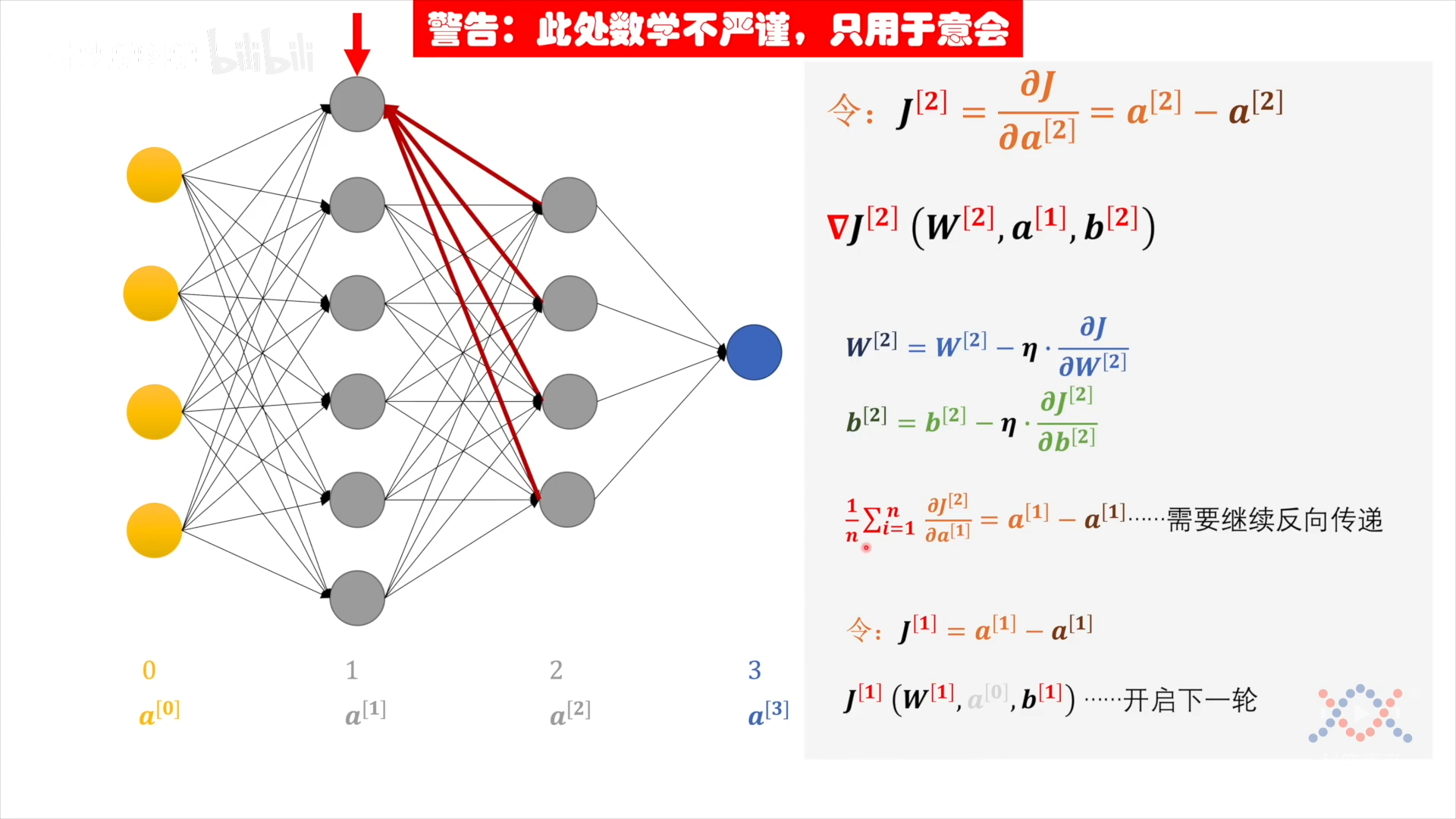
令$J^{[2]}=a^{[2]}{(\rm target)} - a^{[2]}{(\rm now)}$ 作为下一轮的损失函数，对损失函数$J^{[2]}(\mathbf w^{[2]}, \mathbf a^{[1]}, b^{[2]}$)分配：

$$ \begin{aligned} \mathbf w^{[2]} &= \mathbf w^{[2]} - \eta \cdot \frac{\partial J^{[2]}}{\partial \mathbf w^{[2]}} \ b^{[2]} &= b^{[2]} - \eta \cdot \frac{\partial J^{[2]}}{\partial b^{[2]}} \

\frac{1}{n} \sum_{i=1}{n} \frac{\partial J^{[2]}}{\partial \mathbf a^{[1]}} &= a^{[1]}{(\rm target)} - a^{[1]}{(\rm now)} & \text{“$a^{[1]}$的偏差是4个$a^{[2]}$的偏差之平均”} \end{aligned} $$

令 𝑱⁽¹⁾=a₍ₜₐᵣᵨₑₜ₎⁽¹⁾ - a₍ₙₒᵥ₎⁽¹⁾ 作为下一轮的损失函数，对损失函数$J^{[1]}(\mathbf w^{[1]}, \mathbf a^{[0]}, b^{[1]}$)分配，其中 $a^{[0]}$ 是输入，无法修改，只调整 w 和 b。

对于第 $l$ 层的第 $i$ 个感知机，接受上一层所有神经元的输出 $a^{[l-1]}$，与它的 $\mathbf w_i^{[l]}$ 和 $b_i^{[l]}$ 做线性运算得到 $z_{i}^{[l]}$，把 z 送入激活函数得到这个感知机的输出：$\sigma(z_i^{[l]})=a_i^{[l]}$

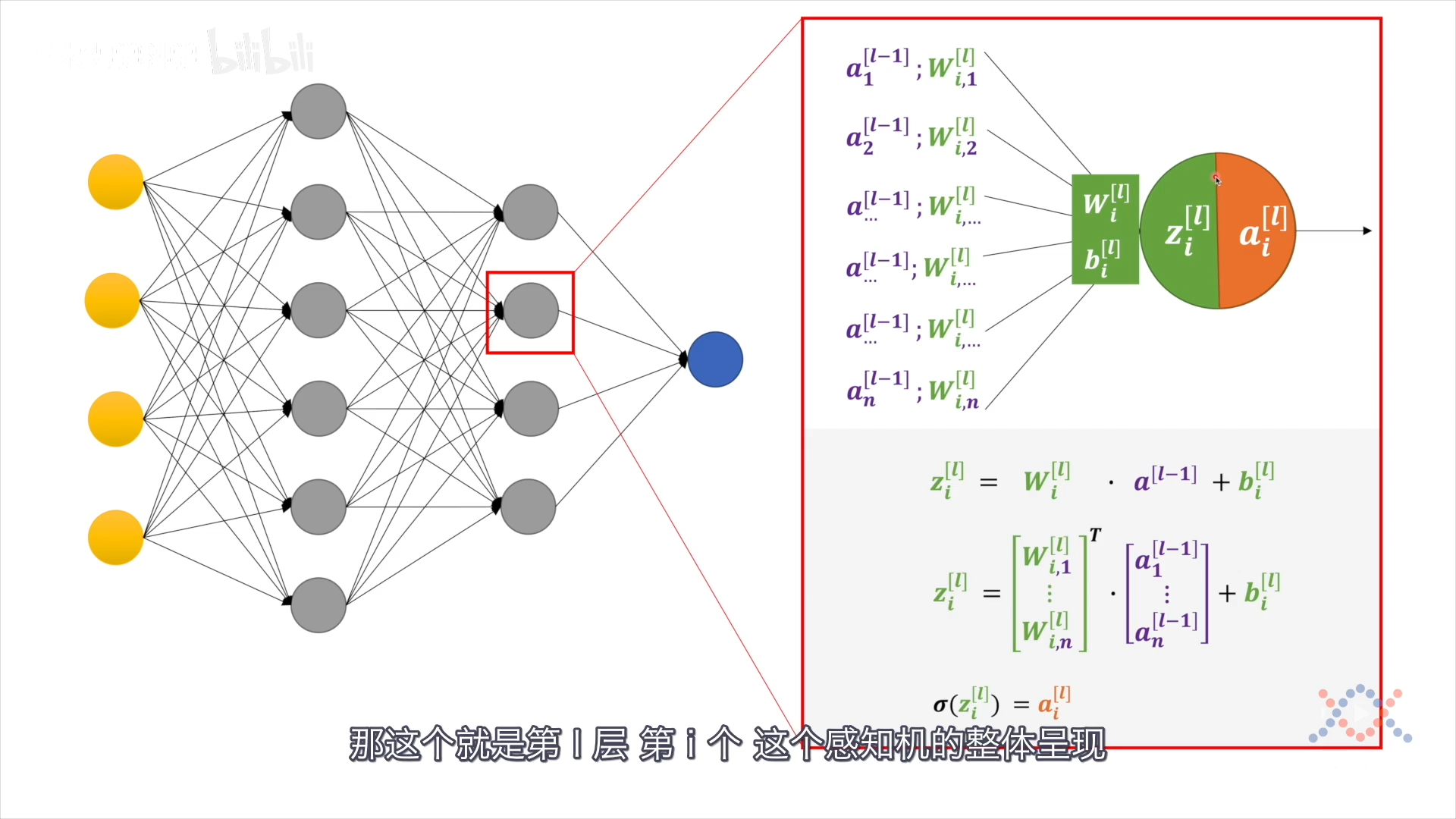
$$ \begin{aligned} z_i^{[l]} &= \mathbf w_i^{[l]} \cdot \mathbf a^{[l-1]} + b_i^{[l]} \ z_i^{[l]} &= \begin{bmatrix} \mathbf w_{i,1}^{[l]} \ \vdots \\mathbf w_{i,n}^{[l]} \end{bmatrix}^T \cdot \begin{bmatrix} a_{1}^{[l-1]} \ \vdots \ a_{n}^{[l-1]} \end{bmatrix} + b_i^{[l]} \end{aligned} $$

对一层感知机进行表述:

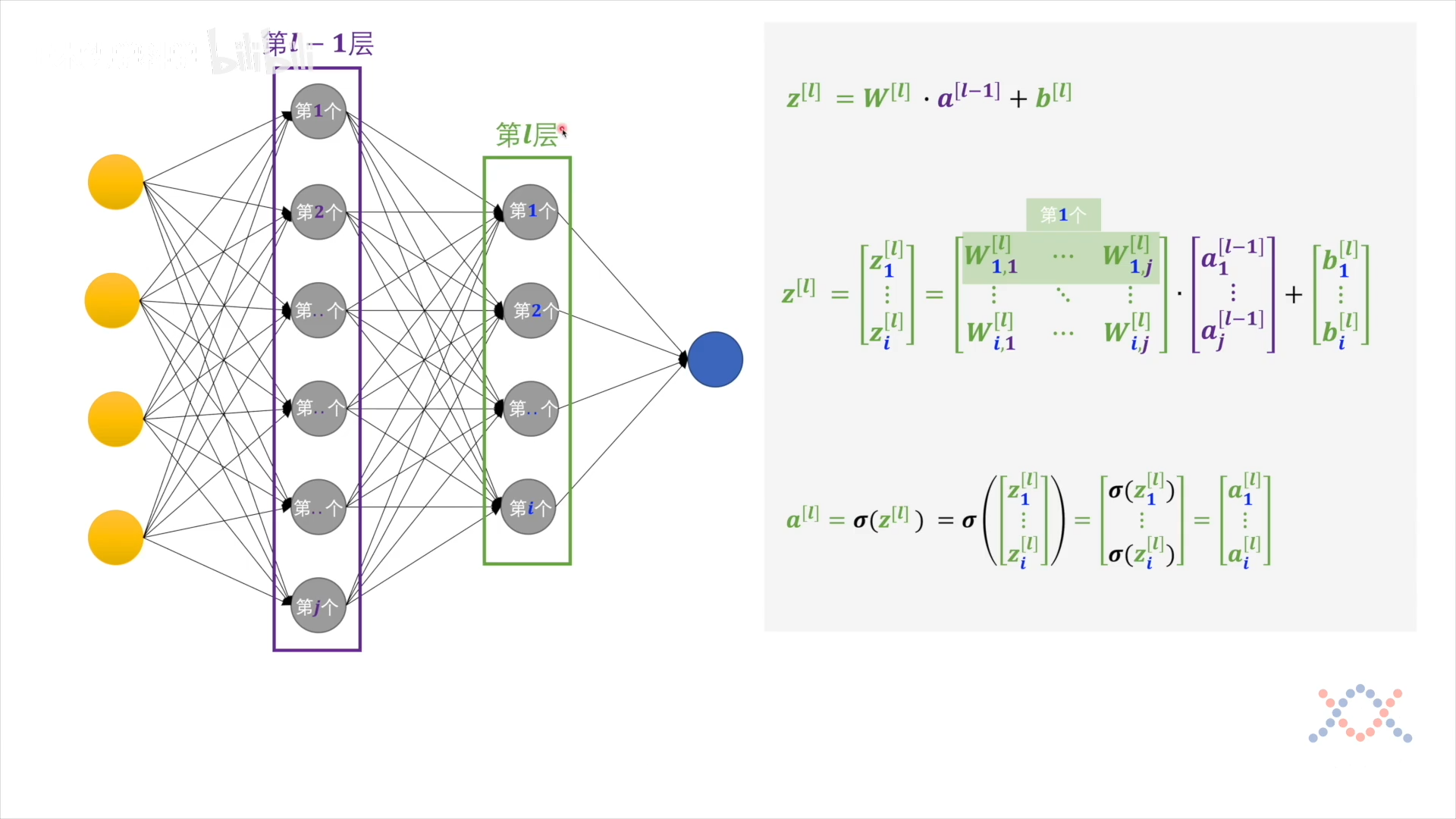
没有下标 $i$ 表示整层，第$l$层各感知机的输出：

$$ \begin{aligned} \mathbf z^{l} &= \mathbf w^{l} \cdot \mathbf a^{l-1} + b^{[l]} \ \mathbf z^{l} &= \begin{bmatrix} z_1^{[l]} \ \vdots \z_i^{[l]} \end{bmatrix} = \begin{bmatrix} \mathbf w_{1,1}^{[l]} & \cdot & \mathbf w_{1,j}^{[l]} \ \vdots & \ddots & \cdots \ \mathbf w_{i,1}^{[l]} & \cdot & \mathbf w_{i,j}^{[l]} \ \end{bmatrix} \cdot \begin{bmatrix} a_1^{[l-1]} \ \vdots \ a_j^{[l-1]} \end{bmatrix} + \begin{bmatrix} b_1^{[l]} \ \vdots \ b_i^{[l]} \end{bmatrix} \

a^{[l]} &=\sigma\left(z^{[l]}\right)=\sigma\left(\left[\begin{array}{c} z_{1}^{[l]} \ \vdots \ z_{i}^{[l]} \end{array}\right]\right)=\left[\begin{array}{c} \sigma\left(z_{1}^{[l]}\right) \ \vdots \ \sigma\left(z_{i}^{[l]}\right) \end{array}\right]=\left[\begin{array}{c} a_{1}^{[l]} \ \vdots \ a_{i}^{[l]} \end{array}\right]

\end{aligned} $$

输出层的损失函数：$J(y,a^{[l]})$，y是label，(k)是第几个样本：

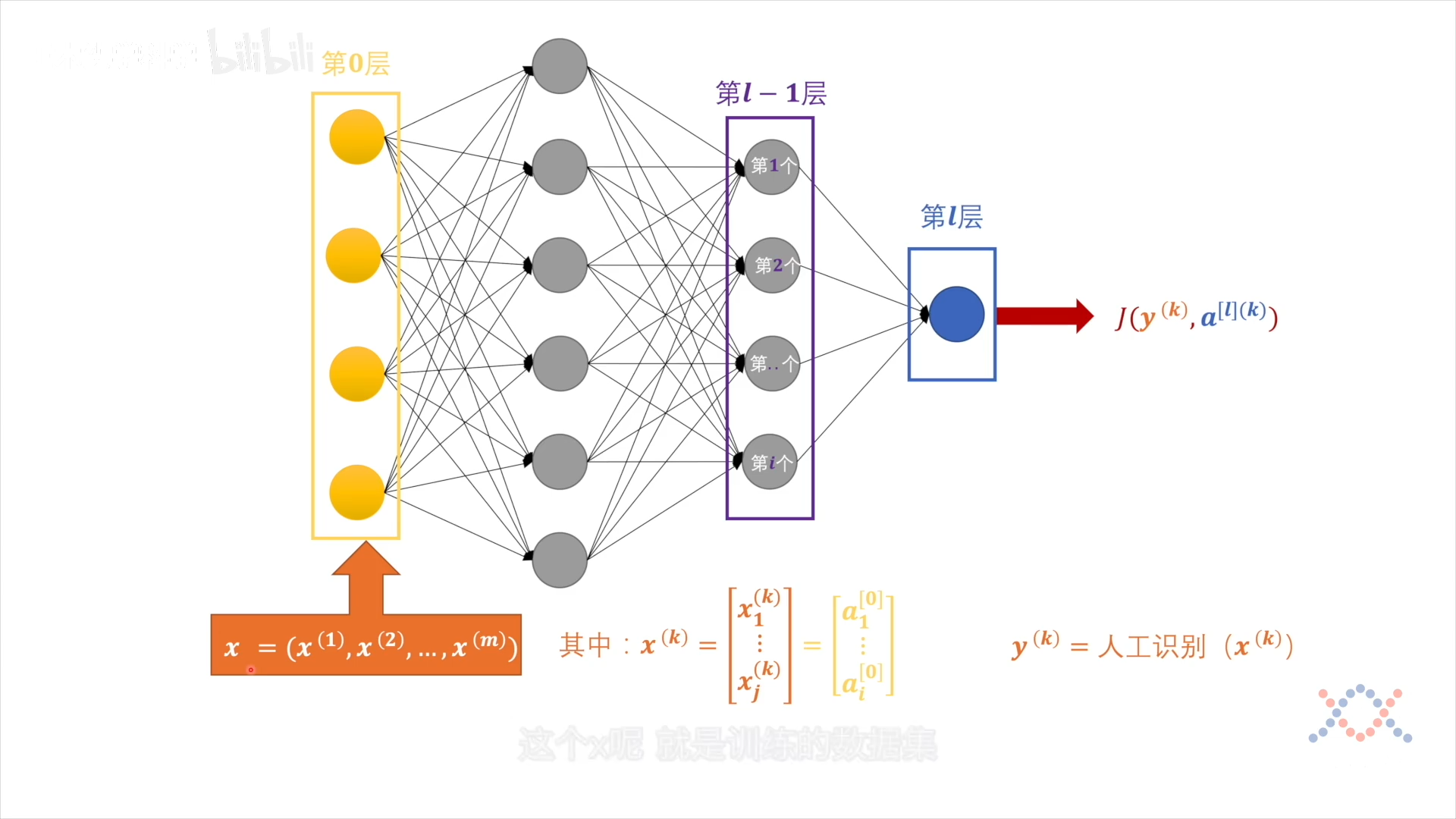
每个样本$\mathbf x$都有 j 个属性，对应第0层的输出 $a^{[0]}$：

$$ a^{[l]}=\sigma\left(z^{[l]}\right)=\sigma\left(\left[\begin{array}{c} z_{1}^{[l]} \ \vdots \ z_{i}^{[l]} \end{array}\right]\right)=\left[\begin{array}{c} \sigma\left(z_{1}^{[l]}\right) \ \vdots \ \sigma\left(z_{i}^{[l]}\right) \end{array}\right]=\left[\begin{array}{c} a_{1}^{[l]} \ \vdots \ a_{i}^{[l]} \end{array}\right] $$

多分类问题，有多个输出 $aᵢ^{l}$，此时的损失函数是把所有输出节点都考虑进来。不考虑常量: 样本x和标签y，损失函数的输出层感知机的函数：

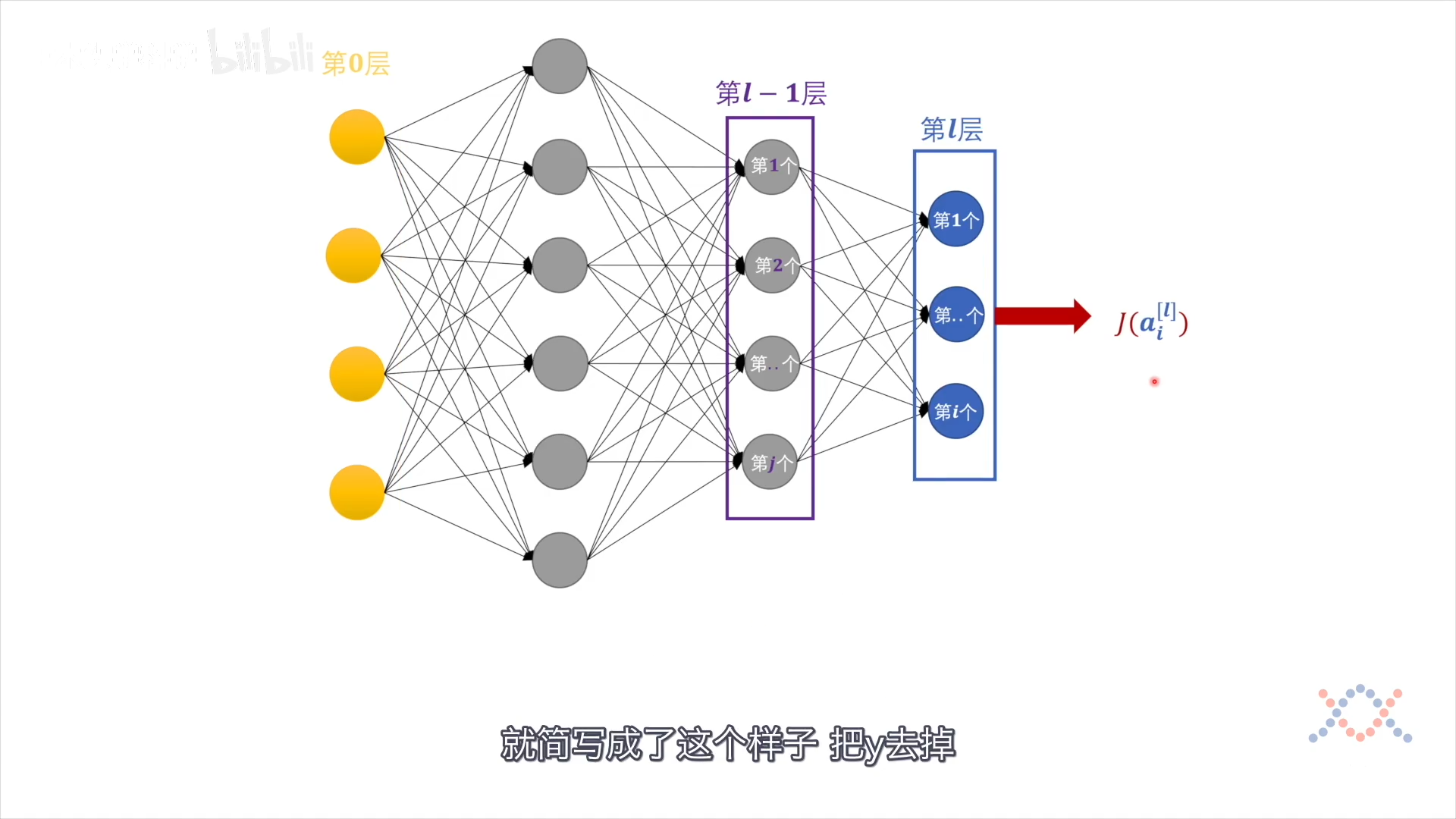
反向传播：对J求梯度，给各变量分配偏差(偏导)，走$eta$步长

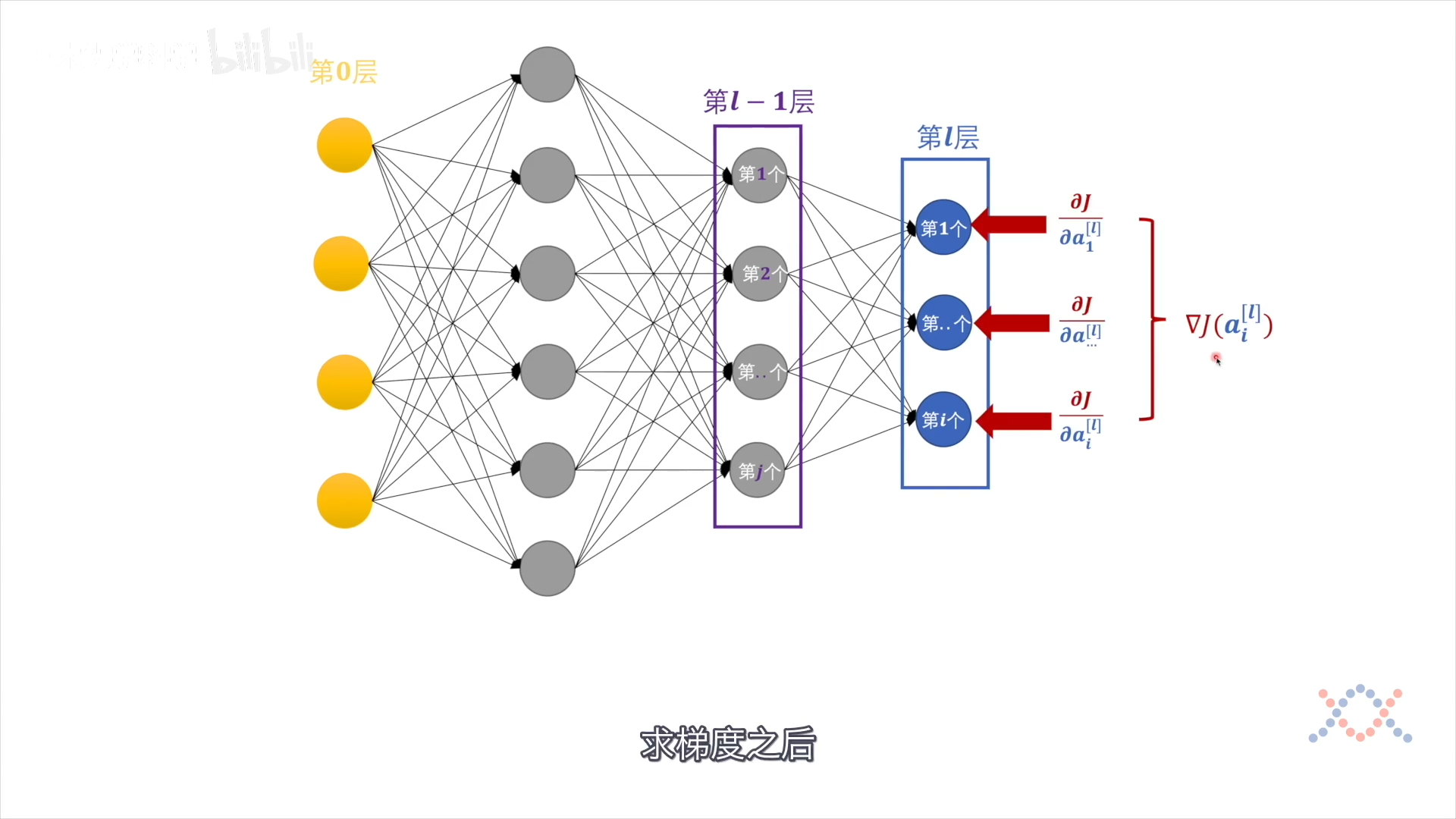
把对输出层各感知机的偏导看作是第 $l+1$ 层，第 l+1 层只对 第l层的一个感知机有作用，$J_1^{[l+1]}$ 是 $\mathbf w_1^{[l]},\ a^{l-1},\ b_1^{l}$ 的函数：

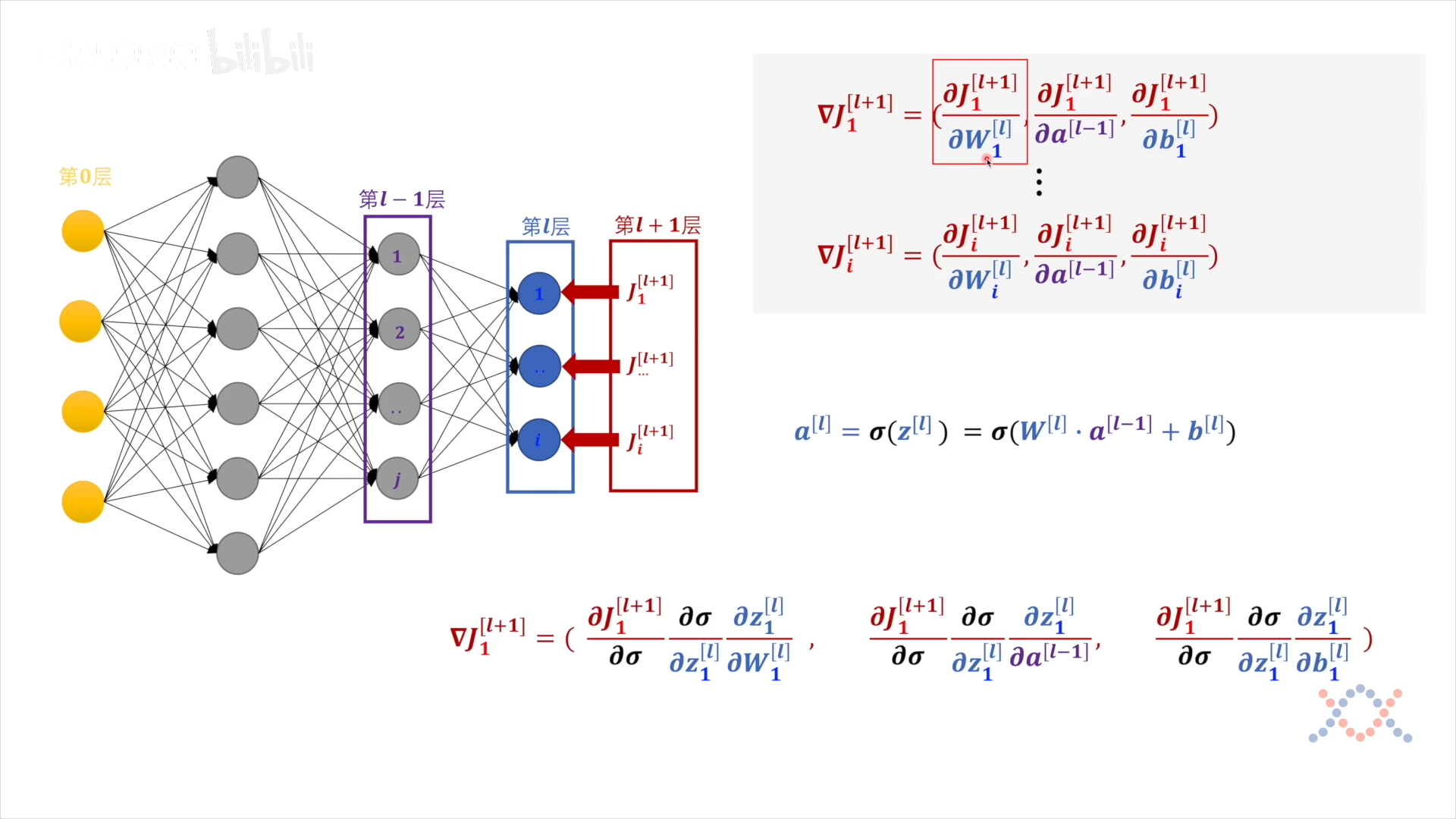
最后$\nabla J$的各项都从输出层 $a$ 开始求导（链式求导）：

$$ \nabla J_{1}^{[l+1]} = \left( \frac{\partial J}{\partial a_{1}^{[l]}} \frac{\partial a_{1}^{[l]}}{\partial \sigma} \frac{\partial \sigma}{\partial z_{1}^{[l]}} \frac{\partial z_{1}^{[l]}}{\partial W_{1}^{[l]}}, \quad \frac{\partial J}{\partial a_{1}^{[l]}} \frac{\partial a_{1}^{[l]}}{\partial \sigma} \frac{\partial \sigma}{\partial z_{1}^{[l]}} \frac{\partial z_{1}^{[l]}}{\partial a^{[l-1]}}, \quad \sqrt{\frac{\partial J}{\partial a_{1}^{[l]}} \frac{\partial a_{1}^{[l]}}{\partial \sigma}} \frac{\partial \sigma}{\partial z_{1}^{[l]}} \frac{\partial z_{1}^{[l]}}{\partial b_{1}^{[l]}} \right) $$

其中 $\mathbf w$ 是向量，对其求偏导要对它的每个分量求偏导：

$$ \begin{array}{l} \frac{\partial J_{1}^{[l+1]}}{\partial W_{1}^{[l]}}=\left(\frac{\partial J_{1}^{[l+1]}}{\partial W_{1,1}^{[l]}}, \frac{\partial J_{1}^{[l+1]}}{\partial W_{1,2}^{[l]}}, \ldots, \frac{\partial J_{1}^{[l+1]}}{\partial W_{1, j}^{[l]}}\right) \ \frac{\partial J_{1}^{[l+1]}}{\partial a^{[l-1]}}=\left(\frac{\partial J_{1}^{[l+1]}}{\partial a_{1}^{[l-1]}}, \frac{\partial J_{1}^{[l+1]}}{\partial a_{2}^{[l-1]}}, \ldots, \frac{\partial J_{1}^{[l+1]}}{\partial a_{j}^{[l-1]}}\right) \end{array} $$

每层的 $\mathbf w$ 和 $b$ 求偏导之后可直接修改：

$$ \begin{array}{c} W_{1}^{[l]}=W_{1}^{[l]}-\eta \cdot \frac{\partial J_{1}^{[l+1]}}{\partial W_{1}^{[l]}} \quad b_{1}^{[l]}=b_{1}^{[l]}-\eta \cdot \frac{\partial J_{1}^{[l+1]}}{\partial b_{1}^{[l]}} \ \vdots \ W_{i}^{[l]}=W_{i}^{[l]}-\eta \cdot \frac{\partial J_{i}^{[l+1]}}{\partial W_{i}^{[l]}} \quad b_{i}^{[l]}=b_{1}^{[l]}-\eta \cdot \frac{\partial J_{i}^{[l+1]}}{\partial b_{i}^{[l]}} \end{array} $$

对 $a^{l-1}$ 求偏导得到的是第 $a^{[l-1]}$ 层的变化量，作为损失函数：

$$ J_{1}^{[l]}=\frac{\partial J_{1}^{[l+1]}}{\partial a^{[l-1]}} \quad \cdots \quad J_{i}^{[l]}=\frac{\partial Jᵢ^{[l+1]}}{\partial a^{[l-1]}} $$

3个窗口反向移动，做下一轮:

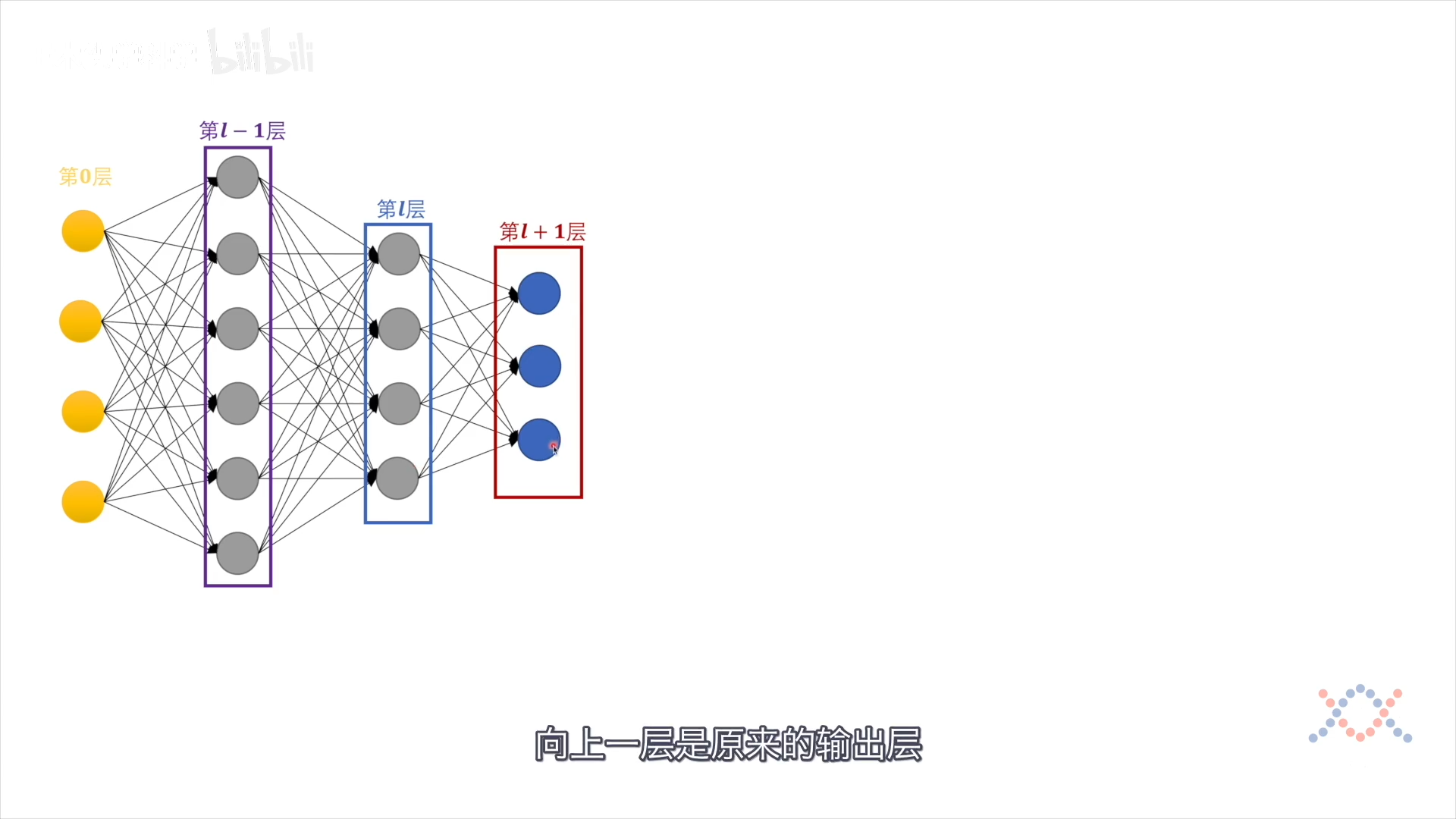
以第2隐藏层为中心，进行分析：

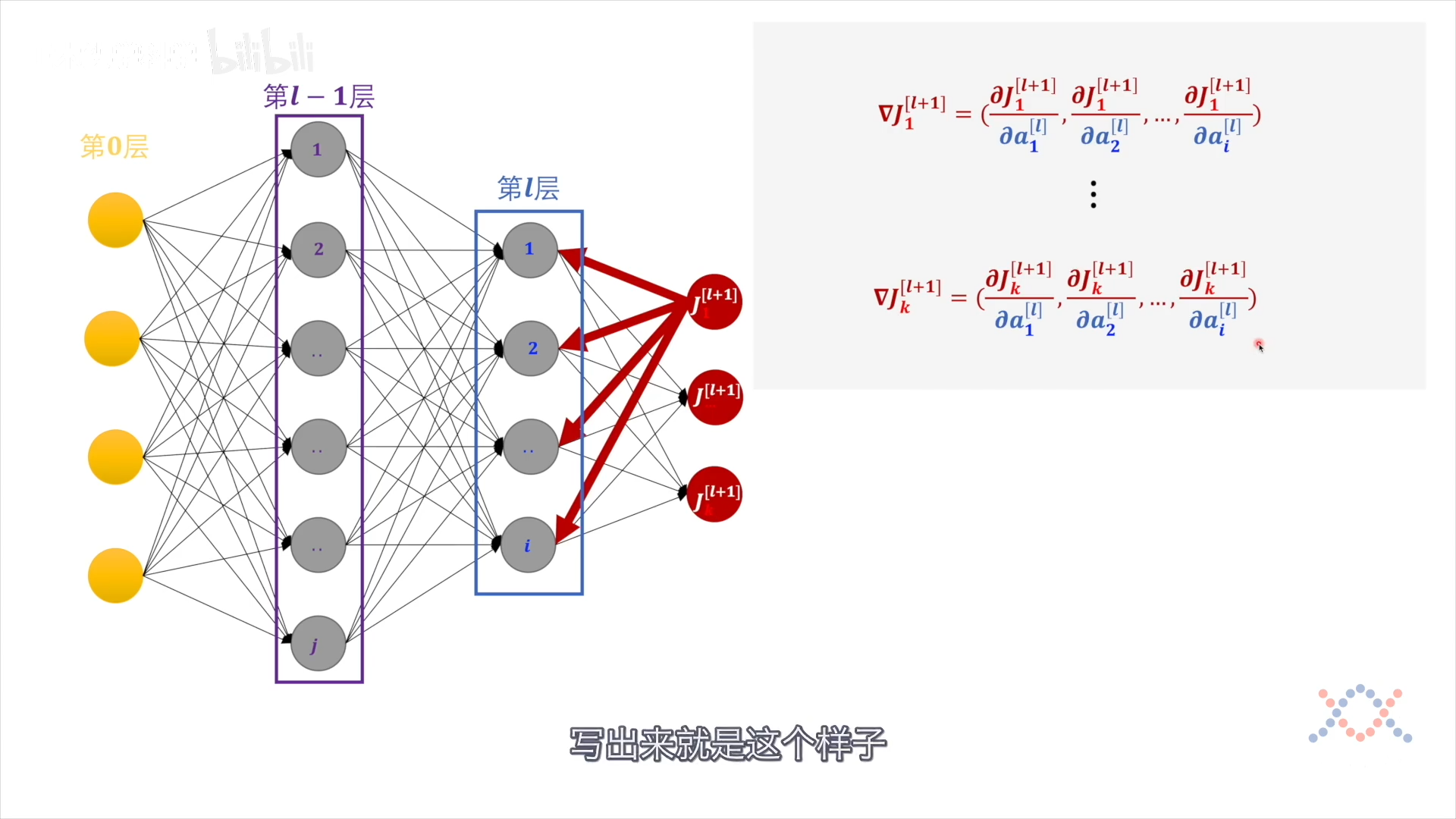
把 a 展开（对a的各分量求偏导）：

$$ \begin{array}{c} \nabla J_{1}^{[l+1]}=\left(\frac{\partial J_{1}^{[l+1]}}{\partial W_{1}^{[l]}}, \frac{\partial J_{1}^{[l+1]}}{\partial a^{[l-1]}}, \frac{\partial J_{1}^{[l+1]}}{\partial b_{1}^{[l]}}, \ldots, \frac{\left.\partial J_{1}^{[l+1]}\right]}{\partial W_{i}^{[l]}}, \frac{\partial J_{1}^{[l+1]}}{\partial a^{[l-1]}}, \frac{\partial J_{1}^{[l+1]}}{\partial b_{i}^{[l]}}\right) \ \vdots \ \nabla J_{k}^{[l+1]}=\left(\frac{\partial J_{k}^{[l+1]}}{\partial W_{1}^{[l]}}, \frac{\partial J_{k}^{[l+1]}}{\partial a^{[l-1]}}, \frac{\partial J_{k}^{[l+1]}}{\partial b_{1}^{[l]}}, \ldots, \frac{\partial J_{k}^{[l+1]}}{\partial W_{i}^{[l]}}, \frac{\partial J_{k}^{[l+1]}}{\partial a^{[l-1]}}, \frac{\partial J_{k}^{[l+1]}}{\partial b_{i}^{[l]}}\right) \end{array} $$

第l层的每个感知机的偏差由第l+1 层的所有偏差值赋予：

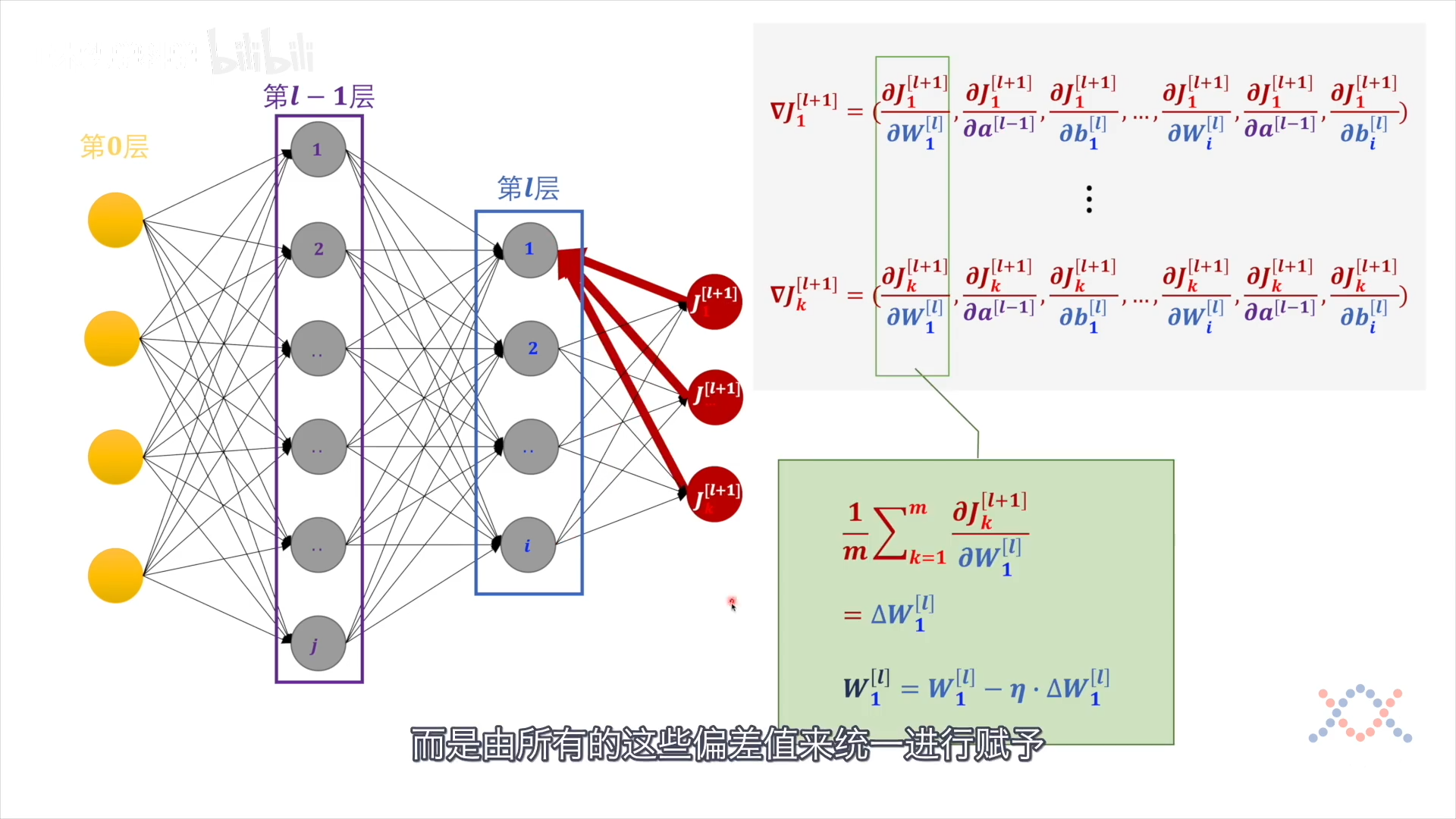
然后第l层各参数的变化量：

$$ \left(\Delta W_{1}^{[l]}, \Delta a^{[l-1]}, \Delta b_{1}^{[l]}, \ldots, \Delta W_{i}^{[l]}, \Delta a^{[l-1]}, \Delta b_{i}^{[l]}\right) $$

$\delta a$ 作为下一轮的损失函数：

$$ \left(\Delta W_{1}^{[l]}, J_{1}^{[l]}, \Delta b_{1}^{[l]}, \ldots, \Delta W_{i}^{[l]}, J_{i}^{[l]} \quad, \Delta b_{i}^{[l]}\right) $$

第2次迭代：

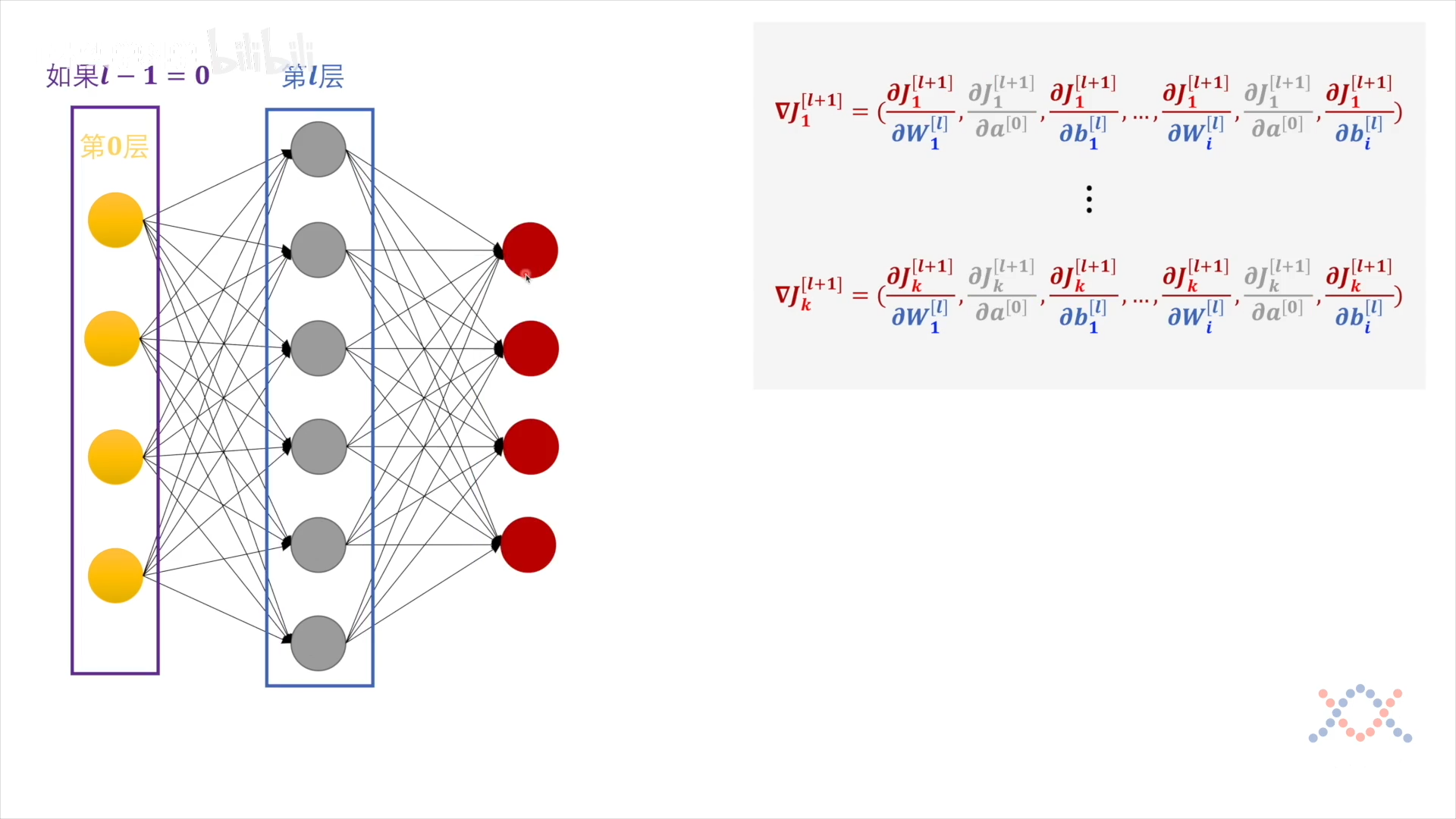
$a^{[0]}$ 是常量输入，求导为零，此时的$J^{l-1}$只与 $\mathbf w$ 和 $b$ 有关:

$$ \begin{array}{c} \nabla J_{1}^{[l+1]}= \left( \frac{\partial J_{1}^{[l+1]}}{\partial W_{1}^{[l]}}, \frac{\partial J_{1}^{[l+1]}}{\partial b_{1}^{[l]}},\ \ldots, \frac{\partial J_{1}^{[l+1]}}{\partial W_{i}^{[l]}}, \frac{\partial J_{1}^{[l+1]}}{\partial b_{i}^{[l]}}\right) \ \vdots \

\nabla J_{k}^{[l+1]}= \left( \frac{\partial J_{k}^{[l+1]}}{\partial W_{1}^{[l]}}, \frac{\partial J_{k}^{[l+1]}}{\partial b_{1}^{[l]}}, \ldots, \frac{\partial J_{k}^{[l+1]}}{\partial W_{i}^{[l]}}, \frac{\partial J_{k}^{[l+1]}}{\partial b_{i}^{[l]}}\right) \ \ \left( \Delta W_{1}^{[l]}, \Delta b_{1}^{[l]}, \ldots, \Delta W_{i}^{[l]}, \Delta b_{i}^{[l]}\right) \end{array} $$