Source video: “随机梯度下降、牛顿法、动量法、Nesterov、AdaGrad、RMSprop、Adam”,打包理解对梯度下降法的优化
梯度下降法在实际应用中的优化:
- 减小每次梯度下降的计算量:随机(分批次)梯度下降
- 减少迭代次数,即优化下降路径
随机梯度下降
对于一个凸问题,时间复杂度与误差量级的关系:
对于一个强凸问题,能收敛得更快
正常情况下,标准梯度下降法(1个batch)应该比随机梯度下降法快,但可以证明,不会快过 1/k
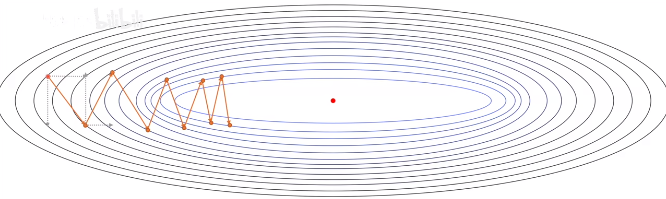
一个 batch 上的损失函数,可能与整个数据集上的损失函数不同,各处对应的梯度也不同, 所以每次迭代时的梯度方向不一定是“全体数据的误差函数”上的最优,每一步的行进可能会偏离下降最快的最优路径,从而导致需要更多次的迭代,才能到达极值点。
如下图,从 A 点 到 A’ 点的最优路径是橙色线,如果分两步,先走到 B ,B 再沿着它的梯度方向走,就走偏了。
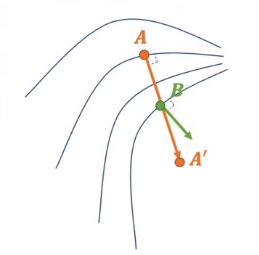
减小步长,可以让下降路径更贴近最优下降路径,但是计算量太大。
牛顿法
牛顿法是用来拟合曲线的,在梯度下降中,就是拟合损失函数表面上的最优下降路径对应的曲线。
对于一个只有一维变量的问题,纵轴是各变量取值对应的误差,蓝色曲线即是损失函数。 要到达损失函数的最小值处,根据梯度下降法,先求出损失函数在当前点的梯度(各个方向分量,按向量加法相加),这里只有一个变量(一个方向),就是求损失函数的切线。 然后变量沿着梯度(切线)方向移动一点,看看此时的误差值。
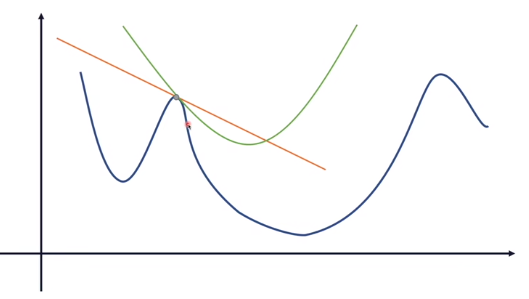
- 抛物线比直线更贴近损失函数,从而使下降路径与损失函数更贴合,而不是折线。
- 因为整个数据集上的损失函数未知,每下降一步,就在当前点的邻域范围内做泰勒展开,用一段高次函数对损失函数做近似代替; 又因为是找下降的方向,所以要保留到二次项,这样就能 拟合出在损失函数(表面)上的下降路径。
- 牛顿法的每一步是确定的:抛物线的顶点对应的横坐标就是这一步要走到的位置,所以牛顿法里没有步长。
下降的方向就不是梯度的方向了?
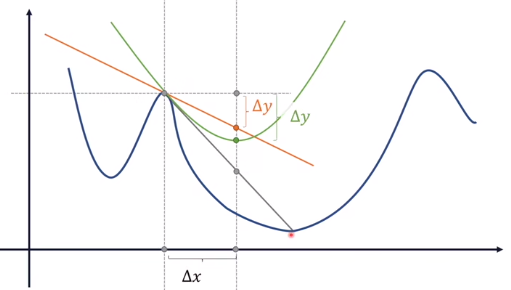
如上图,灰色的直线是到极值点的最优路径,但是未知。 牛顿法希望每一步都走在损失函数上,即拟合出损失函数(表面)上的最优下降路径。
泰勒展开保留二阶导,用二次函数近似表达损失函数上的每一点:
f(x) = J(a₀) + J’(a₀)(x-a₀) + 1/2 J"(a₀)(x-a₀)²
求 f(x) 的极值,就是求顶点所在位置,令 f’(x) = 0:
$$ f’(x) = 0 + J’(a₀) + J"(a₀)(x-a₀) = 0 \\ x = a₀ - J’(a₀) / J"(a₀) $$
然后让变量走到顶点的位置,对应于权重更新:W = W - J’(a₀) / J"(a₀),没有学习率η。 用一阶导数与二阶导数的比值对(一元)变量W做更新。path-int
直观理解:按固定步长做梯度下降法是橙色线,步长无穷小时,下降路径是灰色线,牛顿法的下降路径是绿色线,比梯度下降法更贴近最优路径的灰色线。 所以牛顿法是在拟合最优路径对应的曲线。
对高维函数求二阶偏导,需要算 Hessian 矩阵。对于高维的损失函数 J(W),参数更新公式为: 𝐖 = 𝐖 - 𝛁𝐉²(𝐖)⁻¹ ⋅ 𝛁𝐉(𝐖),其中 𝛁𝐉²(𝐖) 就是 Hessian 方阵 𝐇(𝐖)
$$ 𝐇(𝐖) = \begin{bmatrix} \frac{∂}{∂W₁}\frac{∂f}{∂W₁} & \frac{∂}{∂W₂}\frac{∂f}{∂W₁} & … & \frac{∂}{∂Wₙ}\frac{∂f}{∂W₁}\\ \frac{∂}{∂W₁}\frac{∂f}{∂W₂} & \frac{∂}{∂W₂}\frac{∂f}{∂W₂} & … & \frac{∂}{∂Wₙ}\frac{∂f}{∂W₂}\\ … \\ \frac{∂}{∂W₁}\frac{∂f}{∂Wₙ} & \frac{∂}{∂W₂}\frac{∂f}{∂Wₙ} & … & \frac{∂}{∂Wₙ}\frac{∂f}{∂Wₙ}\\ \end{bmatrix} $$
列向量更新公式:𝐖ₙₓ₁ = 𝐖ₙₓ₁ - 𝐇(𝐖)⁻¹ₙₓₙ ⋅ 𝛁𝐉(𝐖)ₙₓ₁
虽然迭代次数比梯度下降法少,但并不实用,缺点:path-int
- 计算量太大,每一步都要计算n维向量的一阶差分 O(n),Hessian矩阵 O(n²),及其逆
- 不能保证目标函数值在迭代过程中一直下降,可能会先升高,再下降;
- 不能保证收敛:因为牛顿法使用二阶泰勒展开近似,需要初始点在极小点附近,每一步都满足近似条件(Hessian矩阵是正定的),效果才会比较好。 如果离得很远,获得的结果可能非常奇怪。一般应用其他方法先搜索到极小点附近,再用牛顿法(或拟牛顿法)来继续更高精度的搜索。
- 如果目标函数 f(x) 只是一阶可微,二阶不可微(Hessian矩阵不存在),牛顿法就不适用了。 如果二阶可微,理论上牛顿法收敛速度比梯度法要快。牛顿法收敛阶数至少是2,梯度法收敛阶数最差情况下是1。
- 如果是一个多元凸函数,但是不是处处可导,Taylor近似展开不能适应,牛顿法不可应用。
- 若 H 不可逆,需要用 Levenberg-Marquadt 修正:加常量阵 λ𝐈,即给对角线加上足够大的值,使所有的 eigenvalue 都大于0,意味着在任何方向上的一阶导数都大于0. path-int
动量法
牛顿法同时考虑损失函数的所有维度,找出最优下降路径。
梯度是一个多维的向量,可以把各个维度拆开(向量的分解),单独分析每个方向上的变化
加权是要把维度分开考虑
考虑下降两步,抵消相反方向的梯度 惯性 mv,力作用的效果?把速度抵消,减少震荡
前几步梯度大,直接加的话,占主导,而且不准,用一个系数控制前后两个部分的权重就用 beta 和 1-beta (exponentially weighted moving average),越是先前发生的状态,乘以的(1-beta)次数越多,占比越来越小,对当前的值影响越小
Nesterov
等高线坐标系下的点是权重W,Nesterov 把上一时刻的权重按照上一时刻的梯度方向走了一步,没有与当前时刻的梯度加权,把权重点移动到的新位置,这个位置是比如果采用加权时的权重超调一些的,把新位置的梯度带回去,也就是考虑了下一步位置的情况
当前梯度方向d1,历史梯度方向d2,未来梯度方向d3,共同决定向哪个方向走。未来就是先按d2走一步梯度下降,走到一个点,计算那个点的梯度。不是按d1和d2的加权方向走,那样就是提前做了决策,还把决策的结果拿过来用了,应该用历史数据来决策
AdaGrad
当前梯度除以累计历史梯度内积再开根号,梯度的各方向分量数量级不一致,所以除以累计历史梯度模长,梯度值大的那个方向,除以一个数(可能与该方向数值在同一数量级)就没那么大了,不至于在那个方向上走太多,而且分母越加越大,梯度越往后越小。 稀疏数据集:只要关心维度/特征的有无就能把类别分开,而不需关心特征是否明显(猴子和人);非稀疏数据:需要关注同一特征上的差别,在同一特征上的数值,才能分类(长尾猫和短尾猫) 稀疏数据不同样本没有共同的特征,不同特征的绝对值差异大,数值相减后差值大,梯度大
维度越多,越不需要区分在同一特征上的数值差异,只需关心特征的有无,单位球内的点分散到各个维度上了,不再挤在同一维度上了,各个轴上的长度就不用那么长了,所以体积就变小了
王木头解释成学习率的衰减不太合适
梯度按泰勒公式展开,牛顿法用了二次项,动量法修正0次项基础值,AdaGrad修正1次项(梯度变化量)