watch: ML - 白板 11

Gaussian Mixture Model 高斯混合模型

1. 模型介绍

Source video: P1

根据中心极限定理，假设数据服从高斯分布是合理的

一维数据:

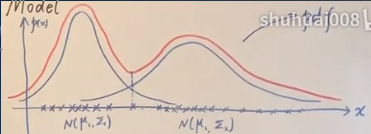
横轴是数据点，服从两个高斯分布的叠加，纵轴是概率密度函数值(PDF)，点越密代表该区域出现样本的概率越大。

可以认为这些样本点服从一个高斯分布，但并不合理，用两个高斯比较精确，红色曲线是2个分布的叠加（混合）。

(1) 从几何角度来看

GMM 的概率密度函数是多个高斯分布的加权平均，并不是直接相加，否则概率密度函数的积分可能大于1。权重是取到各种高斯分布的概率

每个高斯有自己的均值 μ 和方差 Σ （如果是多维的，就是协方差矩阵），它们的参数是要学习出来的。

GMM 中一个样本 x 的概率密度函数是K个高斯分布的加权平均： p(x) = ∑ₖ₌₁ᴷ αₖ N(x|μₖ,Σₖ), where ∑ₖ₌₁ᴷ αₖ = 1，α 是权重

(2) 从混合模型（或概率生成）角度来看

GMM 用离散的随机变量 z 代表样本 x 分别属于 K 个高斯分布概率。N 个样本是重复 N 次生成过程：先从K个高斯分布中选一个，再在这个高斯分布中采样生成一个样本。

两维数据的 PDF 是3维的（曲面）:

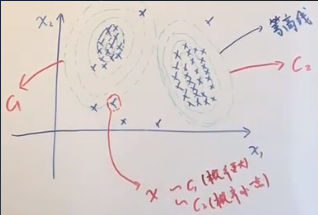
小x 是观测变量observed variable，两维的: x=(x1,x2)
引入隐变量latent variable 小z，一个 z 表明了一个样本 x 可能属于哪一个高斯分布，所以 z 是一个离散型的随机变量，一个样本 x 属于各个高斯分布的概率分别为：

z	C₁	C₂	…	Cₖ
概率密度	p₁	p₂	…	pₖ

z 代表不同的类别categories（不同的高斯分布），其中概率密度求和等于1：∑ₖ₌₁ᴷ pₖ = 1

一个样本既可属于C1，也可属于C2…, 只不过概率不同，所以用一个随机变量表达。用隐变量 z 代表一个样本 x 所属的高斯分布比较方便: x ～ z，z是一个离散分布，可以是 C₁，也可以是 C₂,C₃,…Cₖ,

GMM 是一个生成模型（混合模型一般都是生成模型），每个样本都是按照生成过程逐一生成的：假设有一个骰子有 K 个面，而且重量分布不均匀，所以各面的概率不同（越重越大）

掷一次得到了第 k 面(概率是pₖ)，对应于第 k 个高斯分布
在这第 k 个高斯分布中去采样，就生成了一个样本

GMM 是最简单的生成模型，它的概率图：

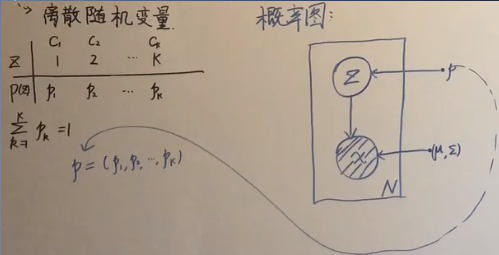
N 表示生成 N 个样本，小 x 是观测变量，用阴影来表示，小 z 是随机变量，用空心的圈表示，它服从的分布是以 p 为参数: p=(p1,p2,…,pₖ) 是一个向量，所以用实心点表示参数 p；而 X 服从高斯分布，其参数为 (μ,Σ)

2. 极大似然

Source video: P2

从混合模型角度，写出 GMM 的概率密度函数 p(x): 既然引入了隐变量 𝐳，也是一个随机变量，把它的概率积掉就行了，又因为 𝐳 是离散型的随机变量，所以是把各个可能的取值求和。

一个样本 x 的概率密度函数：
P(x) = ∑_z P(x,z) = ∑_ₖ₌₁ᴷ P(x,z=Cₖ)，分别从 K 个高斯分布中采出 x 的概率: P(x,zₖ) 累加
= ∑ₖ₌₁ᴷ P(z=Cₖ) P(x|z=Cₖ)，联合概率拆成两项积
= ∑ₖ₌₁ᴷ pₖ ⋅ N(x | μₖ,Σₖ)，第k个高斯分布出现的概率乘以在第k个高斯分布中采出x的概率

所以混合模型的概率密度函数与加权平均是一样的，只不过“权重” aₖ 变成了这里的概率值 pₖ

做 N 次随机试验，每次做试验时(扔骰子)，(假设)隐变量 𝐳 是不同的（即K个正态分布出现的概率不同），每次生成样本时，依据 𝐳 从 K 个高斯分布中选一个分布，再从被选中的高斯分布中采一个 x，所以每个 x 和一个 𝐳 对应: (xᵢ,𝐳ᵢ)。要求 xᵢ 的似然，就把这次试验中的 𝐳ᵢ 从联合概率P(xᵢ,𝐳ᵢ)中积掉。

N个样本就是 N 次试验同时发生，发生的概率（似然）就是多次试验的连乘 P(X,Z)=p(x₁,z₁)p(x₂,z₂)…p(xN,zN))，所以求 P(X)=∫z P(X,Z) dZ 就是多重积分: 先对 z1 积，再对 z2 积，….

x observed variable, 观测随机变量
z latent variable, 隐变量，服从离散分布: K个类别（高斯分布）C₁,C₂,…,Cₖ 分别对应概率 p₁,p₂,…,pK；
X observed data, N个观测数据 x1,x2,…xN, 样本之间相互独立
Z “latent data”, z1,z2,…zN, N 个样本 x 对应的生成它的隐变量
(X,Z): complete data, “完整数据” (x1,z1),(x2,z2),…(xN,zN)，每个样本 x 对应一个隐变量
为了叙述方便，用 θ 代表参数 = {p₁,p₂,…,pK, μ₁,Σ₁, μ₂,Σ₂,…, μK,ΣK}，隐变量中 K 个高斯分布出现的概率 + K 个高斯的均值和方差

用极大似然估计参数 θ: θ^ = arg max_θ log P(X)

GMM 是没有解析解的，所以直接用 MLE 是做不出来的，只能用数值方法得到近似解。而且 GMM （混合模型）中含有隐变量，所以用 EM 算法（迭代）会更有效率。

θ^ = arg max_θ log P(X) = arg max_θ log ∏ᵢ₌₁ᴺ P(xᵢ) ，N个样本iid
= arg max_θ ∑ᵢ₌₁ᴺ log P(xᵢ) ，连乘变连加
= arg max_θ ∑ᵢ₌₁ᴺ log ( ∑ₖ₌₁ᴷ pₖ ⋅ N(xᵢ | μₖ,Σₖ) )，将P(xᵢ)代入

要求极大值对应的参数，可以对上式中的参数（pk,μₖ,Σₖ）求偏导=0，但是因为 log 里面是多项连加，而且高斯分布可能是高维的（表达式很复杂），无法求出解析解

对于单个高斯分布，它的μ,σ² 都可以直接用 MLE 求出来。因为单一个正态分布的表达式简单，log可以把两项之积拆开，也可以把exp去掉，简化之后，对似然求导，可得到解析解。

3. EM求解-E-step

Source video: P3

用 EM 算法通过 MLE 求出 GMM 的参数 θ。

EM 是要最大化似然的下界，即似然的期望：θ⁽ᵗ⁺¹⁾ = arg max_θ ∫_Z q(Z) ⋅ log P(X,Z|θ) dZ，这个积分的本意是对（每个样本的）似然值 log P(x,z|θ) 按照隐变量 z 的分布 q(z) 求期望。因为 z 的分布是离散的，包括 K 个（高斯分布出现的）概率值，所以 logP(x,z|θ) 和 q(z) 也都是离散的，二者相乘的积分就是加权和 ∑ q(z)⋅log P(x,z|θ)，就是一个样本的期望。

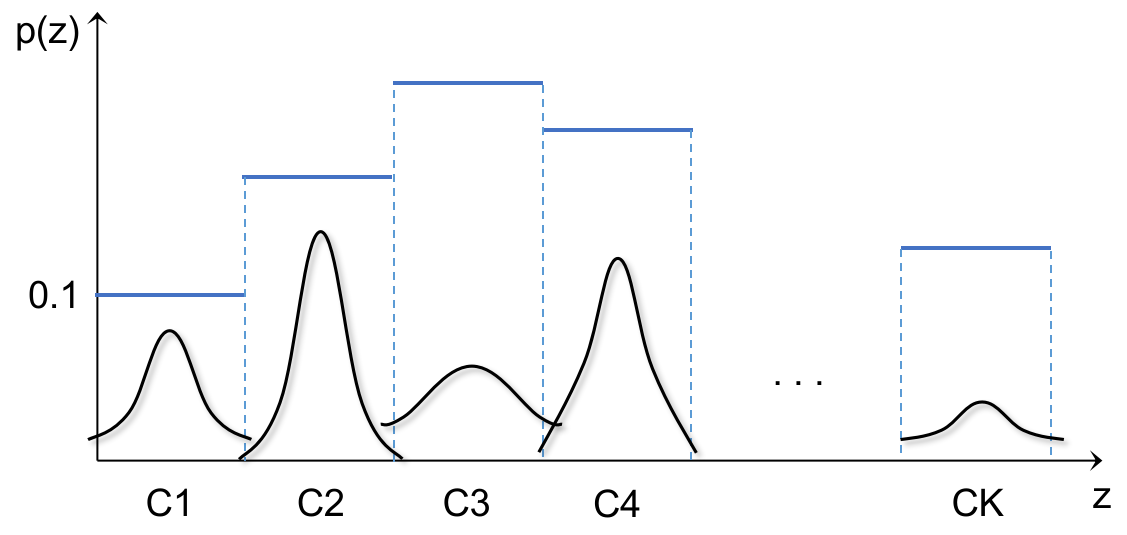
因为大 Z 是多个小 z 的联合，是多个”事件“同时发生的联合概率，又因为样本之间独立同分布，大Z的概率就是单个 z 的概率连乘：q(Z)=q(z₁)⋅q(z₂)…q(zN)，所以对大 Z 的积分就是多重积分，即对每个小 z 积分: ∫z₁∫z₂…∫zN；而只做有限 N 次试验的话，就是把 N 次实验的加权和连乘起来：

E = ∫_Z q(Z) ⋅ log P(X,Z|θ) dZ ，X和Z都是大写, N个样本集合. (|也可写成;: θ是随机变量vs固定值 ¹)
= ∫_z₁ ∫_z₂…∫_zN q(Z) ⋅ log P(X,Z|θ) dz₁ dz₂ dzN，把q(Z)写开
= ∑_z₁ ∑_z₂…∑_z$_N$ ∏ᵢ₌₁ᴺ q(zᵢ) ⋅ log ∏ᵢ₌₁ᴺ P(xᵢ,zᵢ|θ)，zᵢ都是离散分布
= ∑_z₁ ∑_z₂…∑_z$_N$ ∏ᵢ₌₁ᴺ P(zᵢ|xᵢ,θ⁽ᵗ⁾) ⋅ log ∏ᵢ₌₁ᴺ P(xᵢ,zᵢ|θ) ，当 q(zᵢ) 等于Z的后验分布时，KL散度=0，“积分”（似然的期望）取到最大。
= ∑_z₁ ∑_z₂…∑_z$_N$ [ ∏ᵢ₌₁ᴺ P(zᵢ|xᵢ,θ⁽ᵗ⁾) ⋅ ∑ᵢ₌₁ᴺ log P(xᵢ,zᵢ|θ) ]，log连乘变连加

把这个期望 E 记为 Q(θ,θ⁽ᵗ⁾)，是关于 θ 的一个函数（log 中的 θ 是变量，而θ⁽ᵗ⁾是常数）。

先把 log 的连加展开：

Q(θ,θ⁽ᵗ⁾) = ∑_z₁ ∑_z₂…∑_z$_N$ ∏ᵢ₌₁ᴺP(zᵢ|xᵢ,θ⁽ᵗ⁾) ⋅ [ log P(x₁,z₁|θ) + log P(x₂,z₂|θ) + … + log P($x_N,z_N$|θ)]

多重"积分"，先对 z₁ 积分：先只取出第 1 项 logP(x₁,z₁|θ)，并且只把 z₁ 从联合概率中取出来：

∑_z₁ ∑_z₂…∑_z$_N$ [ log P(x₁,z₁|θ) ⋅ ∏ᵢ₌₁ᴺ P(zᵢ|xᵢ,θ⁽ᵗ⁾) ]

对于后半部分的从 2 到 N 的联合概率：

∑_z₂…∑_zN [ ∏ᵢ₌₂ᴺ P(zᵢ|xᵢ,θ⁽ᵗ⁾) ]
= ∑_z₂…∑_zN [ P(z₂|x₂,θ⁽ᵗ⁾) ⋅ P(z₃|x₃,θ⁽ᵗ⁾) … ⋅ P(zN|xN,θ⁽ᵗ⁾)]

因为每一个累加号都只与一个 z 相关，也就是把每个 z 对应的离散概率分布（p₂,…,pK）求和，并且概率密度函数积分等于 1:
= ∑_z₂ P(z₂|x₂,θ⁽ᵗ⁾) ∑_z₃ P(z₃|x₃,θ⁽ᵗ⁾) … ∑_zN P(zN|xN,θ⁽ᵗ⁾)
= 1⋅1⋅…⋅1 = 1

所以对 z₁ 积分的结果，除了只与 z1 相关的项: ∑_z₁ logP(x₁,z₁|θ) ⋅ P(z₁|x₁,θ⁽ᵗ⁾)，其余都是1。同理之后对 z2, z3,…zN积分时，也只保留与自己相关的项

Q(θ,θ⁽ᵗ⁾) = ∑_z₁∑_z₂…∑_zN ∏ᵢ₌₁ᴺ P(zᵢ|xᵢ,θ⁽ᵗ⁾) ⋅ [logP(x1,z1|θ) + logP(x2,z2|θ) +… + logP(x_N,zN|θ)]

综上，似然P(X)的期望等于 N 个样本的似然期望的和。

把似然和后验代入 Q:

Q(θ,θ⁽ᵗ⁾) = ∑ᵢ₌₁ᴺ ∑_zᵢ log (p_zᵢ ⋅ N(xᵢ | μ_zᵢ,Σ_zᵢ)) ⋅ [ p_zᵢ ⋅ N(xᵢ | μ_zᵢ,Σ_zᵢ) / ∑ₖ₌₁ᴷ pₖ ⋅ N(xᵢ | μₖ,Σₖ) ] ，zᵢ是1⋯K中的任意一个

以上就是 EM 中的 E-step：把（N个样本的）似然的期望表示出来。M-step 要关于参数 θ 求 Q 的最大值。

4. EM求解-M-step

Source video: P4

上面得到了 Q 的表达式，对每个样本的似然按照后验求期望，然后N个样本累加。 M-step 要解一个最优化问题。

后验展开是：p_zᵢ ⋅ N(xᵢ | μ_zᵢ⁽ᵗ⁾,Σ_zᵢ⁽ᵗ⁾) / ∑ₖ₌₁ᴷ pₖ⁽ᵗ⁾ ⋅ N(xᵢ | μₖ⁽ᵗ⁾,Σₖ⁽ᵗ⁾)

在后续推导中，仍然把一个样本z 的后验简记为： P(zᵢ|xᵢ,θ⁽ᵗ⁾)，因为 θ⁽ᵗ⁾是上一时刻的参数：θ⁽ᵗ⁾={p₁⁽ᵗ⁾,p₂⁽ᵗ⁾,…,pK⁽ᵗ⁾, μ₁⁽ᵗ⁾,Σ₁⁽ᵗ⁾, μ₂⁽ᵗ⁾,Σ₂⁽ᵗ⁾,…, μ_K⁽ᵗ⁾,Σ_K⁽ᵗ⁾}，是常数，所以就简单写。而似然 logP(xᵢ,zᵢ|θ) 中的θ 是变量，所以似然的期望的累加就表示为：

Q(θ,θ⁽ᵗ⁾) = ∑ᵢ₌₁ᴺ ∑_zᵢ log (p_zᵢ ⋅ N(xᵢ | μ_zᵢ, Σ_zᵢ)) ⋅ P(zᵢ|xᵢ, θ⁽ᵗ⁾)

交换两个累加符号顺序：

Q(θ,θ⁽ᵗ⁾) = ∑_zᵢ ∑ᵢ₌₁ᴺ log (p_zᵢ ⋅ N(xᵢ | μ_zᵢ, Σ_zᵢ)) ⋅ P(zᵢ|xᵢ, θ⁽ᵗ⁾)

zᵢ 是一个样本上，K个高斯分布可能的概率，z 在最外面，可以把 zᵢ 替换成小 k（从1到K），∑_zᵢ 替换为 ∑ₖ₌₁ᴷ：

Q(θ,θ⁽ᵗ⁾) = ∑ₖ₌₁ᴷ ∑ᵢ₌₁ᴺ log (pₖ ⋅ N(xᵢ | μₖ, Σₖ)) ⋅ P(zᵢ=Cₖ|xᵢ, θ⁽ᵗ⁾)
= ∑ₖ₌₁ᴷ ∑ᵢ₌₁ᴺ [ log pₖ + log N(xᵢ | μₖ, Σₖ) ] ⋅ P(zᵢ=Cₖ|xᵢ, θ⁽ᵗ⁾)

目标函数就为： θ⁽ᵗ⁺¹⁾ = arg max_θ Q(θ,θ⁽ᵗ⁾)

θ⁽ᵗ⁺¹⁾ 包括 pₖ⁽ᵗ⁺¹⁾={p₁⁽ᵗ⁺¹⁾,p₂⁽ᵗ⁺¹⁾,…,p_K⁽ᵗ⁺¹⁾}, μₖ⁽ᵗ⁺¹⁾={μ₁⁽ᵗ⁺¹⁾,μ₂⁽ᵗ⁺¹⁾,…,μ_K⁽ᵗ⁺¹⁾}, Σₖ⁽ᵗ⁺¹⁾={Σ₁⁽ᵗ⁺¹⁾,Σ₂⁽ᵗ⁺¹⁾,Σ_K⁽ᵗ⁺¹⁾}，

下面只介绍 pₖ 的求法：

在 Q(θ,θ⁽ᵗ⁾) 中，只有 log pₖ 与 pₖ 相关：

p⁽ᵗ⁺¹⁾ = arg max_pₖ ∑ₖ₌₁ᴷ ∑ᵢ₌₁ᴺ log pₖ ⋅ P(zᵢ=Cₖ|xᵢ,θ⁽ᵗ⁾), s.t. ∑ₖ₌₁ᴷpₖ=1

求这个带约束的最优化问题，用拉格朗日乘子法求解:

写出拉格朗日函数：

L(pₖ,λ) = ∑ₖ₌₁ᴷ ∑ᵢ₌₁ᴺ log pₖ ⋅ P(zᵢ=Cₖ|xᵢ,θ⁽ᵗ⁾) + λ(∑ₖ₌₁ᴷpₖ - 1)

对 pₖ 求偏导时，后面的z的后验分布是常量，求导后是系数。pₖ 的 k 是从1到K的任一数，只对 pₖ 求导，所以带有 p₁,p₂,…, pₖ₋₁ 的项都是0，即最外层的累加号没了。

∂L/∂pₖ = ∑ᵢ₌₁ᴺ 1/pₖ ⋅ P(zᵢ=Cₖ|xᵢ,θ⁽ᵗ⁾) + λ ≜ 0 ，令其等于0

两边同时乘以 pₖ:

∑ᵢ₌₁ᴺ P(zᵢ=Cₖ|xᵢ,θ⁽ᵗ⁾) + pₖ ⋅ λ = 0

为了利用约束条件，把 k=1,2,…,K 的式子都加起来：

∑ᵢ₌₁ᴺ ∑ₖ₌₁ᴷ P(zᵢ=Cₖ|xᵢ,θ⁽ᵗ⁾) + ∑ₖ₌₁ᴷpₖ ⋅ λ = 0

其中 ∑ₖ₌₁ᴷ P(zᵢ=Cₖ|xᵢ,θ⁽ᵗ⁾) 是对隐变量 zᵢ 的概率密度函数“积分”，为1，所以

∑ᵢ₌₁ᴺ 1 + λ = 0
λ = -N

把 λ=-N 代入上式：

∑ᵢ₌₁ᴺ P(zᵢ=Cₖ|xᵢ,θ⁽ᵗ⁾) + pₖ ⋅ (-N) = 0

pₖ⁽ᵗ⁺¹⁾ = 1/N ⋅ ∑ᵢ₌₁ᴺ P(zᵢ=Cₖ|xᵢ,θ⁽ᵗ⁾)

上式是通项，把 k=1,2,..K，代入就可得到每个 p。

求 μₖ 和 Σₖ 的方法类似，只关心 log N(xᵢ | μₖ,Σₖ)，log 可以把高斯分布的概率密度函数简化（两项积拆成两项和，exp也可去掉），而且是无约束，直接（关于矩阵）求导，令其=0就行

Ref

概率论：p(x|theta)和p(x;theta)的区别 - -柚子皮- - CSDN