Featured image of post watch: CppExt - AI葵 | CUDA Extension for PyTorch

watch: CppExt - AI葵 | CUDA Extension for PyTorch

watch: CppExt - AI葵 01 | Cpp Bridges PyTorch & CUDA

Source video: Pytorch+cpp/cuda extension 教學 tutorial 1 - English CC -

Instructions

The pure purpose of CUDA extensions is to make PyTorch programs faster.

CUDA extensions are more efficient than PyTorch in two scenarios:

  1. Procedures can’t be executed in parallel, e.g., each ray has different numbers of points.

  2. Many sequential computations, like a nn.Sequential module including lots of conv layers. C++ can fuse multiple layers to a single function.

Relations: PyTorch will call a C++ function, which will call the CUDA extension.

P y T o r c h " B C r p i p d g e " C U D A

Environment

  1. conda create -n cppcuda python=3.8

  2. Latest PyTorch: conda install pytorch==1.12.1 cudatoolkit=10.2 -c pytorch

    Version of the (compiled) PyTorch needs to match the local CUDA version (checked by nvcc -V).

  3. Upgrade pip for building cpp programs: python -m pip install pip -U

Pybind11

The code: “interpolation.cpp” acts like the main function that calls the C++ function, and python will call the “main” function. The “main” function receives input tensors from PyTorch and return output tensors from CUDA code.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

// Declare PyTorch
#include <torch/extension.h>

// Define starts with the type of return values
torch::Tensor trilinear_interpolate(
    torch::Tensor features, // 8 corners
    torch::Tensor point     // target point coord. No comma at the end
){
    return features;
}

// API for Python
PYBIND11_MODULE(TORCH_EXTENSION_NAME, m){
    // Function name in python and the cpp function
    m.def("trilinear_interpolate", &trilinear_interpolate);
}

  • (2023-10-18) Didn’t update the includePath for PyTorch as follows because I didn’t find the entry “C/C++: Edit Configurations (JSON)” after pressing F1. It seems like VSCode finds PyTorch automatically.

    1
2
3
4
5
6

    "includePath": [
  "${workspaceFolder}/**",
  "/home/yi/anaconda3/envs/AIkui/include/python3.10",
  "/home/yi/anaconda3/envs/AIkui/lib/python3.10/site-packages/torch/include",
  "/home/yi/anaconda3/envs/AIkui/lib/python3.10/site-packages/torch/include/torch/csrc/api/include"
],

  • (2023-10-27) However, error intellisense occurs after I installed the ‘C/C++ Extension Pack’ for VSCode. So setting includePath is necessary.

  • pybind11 connects Python and C++11 codes.

    1
2

    pip install pybind11
pip install ninja

Pip compile

Build the cpp codes to a python package.

  1. Create a “setup.py” for building settings.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

    from setuptools import setup
from torch.utils.cpp_extension import BuildExtension, CppExtension

setup(
    name="my_cppcuda_pkg",    # python package name
    version="0.1",
    description="cppcuda example",
    long_description="cpp-cuda extension",
    author="z",
    author_email="luckily1640@gmail.com",
    ext_modules=[
        CppExtension(
            name='my_cppcuda_pkg', 
            sources=["interpolation.cpp",]) # code files
    ],
    cmdclass={  # commands to be executed
        "build_ext":BuildExtension
        } 
)

  2. Build and install the package:

    1
2
3
4

    pip install .    # setup.py path is cwd (since pip 21.3)

# Or adding an arg to avoid the deprecation warning:
pip install . --use-feature=in-tree-build

(2024-03-06) Pybind11 module also can be compiled with cmake: 如何在Python中调用C++代码？pybind11极简教程 - HexUp

PyTorch Call

“test.py” will call the cpp program.

  • Package torch must to be imported before the cuda extensions.
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

import torch

import my_cppcuda_pkg

features = torch.ones(8,1)
point = torch.zeros(1,2)

out = my_cppcuda_pkg.trilinear_interpolate(features, point)

print(out)

title: “watch: CppExt - AI葵 02 | Kernel Function” date: 2023-10-23T20:20:00

GPU Parallsiam

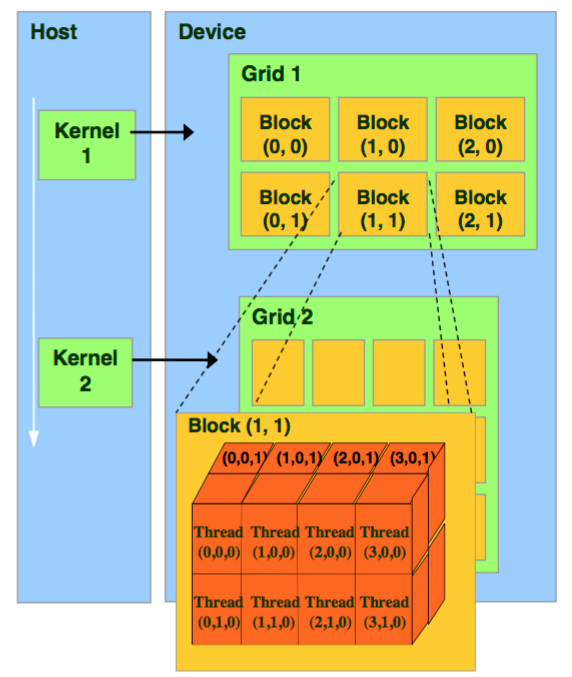
Kernel → Grid → Block → Thread

C P K n U e e r l d a t a ⋮ G P G U r i B d l T o c h k r 0 e a d B l T o c h k r 1 e a d ⋅ ⋅ ⋅

  • A thread is the smallest computation unit that executes element arithmatic independently.

  • The number of threads in a block is limited up to 1024. To multiply the amount of threads, many Block are placed together in a Grid. Docs

    The number of Blocks can be $(2^{31}-1) × 2^{16} × 2^{16}$

  • Introducetion to GPUs - NYU

Trilinear Interpolate

Each corner is sumed up with a weight which is the product of normalized distance from the point to the opposite side.

  1. Analogy to Bilinear interpolation:

    f f ₁ ₃ = = = = = u = = 1 = - 1 v = v ‖ 1 - u f 1 f ₂ ₄

    $$\rm f(u,v) = (1-u)(1-v)⋅f₁ + u(1-v)⋅f₂ + (1-u)v⋅f₃ +uv⋅f₄$$

  2. For Trilinear interpolation, each weight is the product of 3 normalized distances to the opposite plane.

    $$ \begin{aligned} \rm f(u,v,w) =& (1-u)(1-v)(1-w)f₁ + u(1-v)(1-w)f₂ + (1-u)v(1-w)f₃ + uv(1-w)f₄ \\ &+ (1-u)(1-v)w f₅ + u(1-v)w f₆ + (1-u)vw f₇ + uvwf₈ \\ & \\ =&\rm (1-u) [ (1-v)(1-w)f₁ + v(1-w)f₃ +(1-v)wf₅ +vw f₇ ] \\ &\rm + u [ (1-v)(1-w)f₂ + v(1-w)f₄ + (1-v)w f₆ + vwf₈] \end{aligned} $$

    f f ₁ ₃ f f ₅ ₇ u w V f f ₄ ₂ f f ₆ ₈

Input-Output

  1. Input: features (N, 8, F) and points coordinates in each cube (N, 3)

    Output: features at points (N, F).

  2. Operations can be performed in parallel

    1. Each point can be computed individually;
    2. Each feature can be computed individually.

Code

Notes:

  • If input variables of CUDA kernel are torch.Tensor, they must be checked whether they’re on cuda and contiguous, because threads needs to read/write data without jumping.

    While if input variables are not tensor, the checking is not required.

cpp

Cpp: “trilinear_interpolate.cpp”

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

#include <torch/extension.h>
#include "utils.h"

torch::Tensor trilinear_interpolate(
    const torch::Tensor features,
    const torch::Tensor points
){
    // Check input tensors for building successfully
    CHECK_INPUT(features);
    CHECK_INPUT(points);

    // Call the cuda kernel
    return trilinear_fw_cu(features, points);
}

PYBIND11_MODULE(TORCH_EXTENSION_NAME, m){
    m.def("trilinear_interpolate", &trilinear_interpolate);
}

Header: “include/utils.h”

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

#include <torch/extension.h>

// "one-line functions"
// Any tensor must reside on cuda device.
#define CHECK_CUDA(x) TORCH_CHECK(x.is_cuda(), #x " must be a CUDA tensor")

// Next element in x corresponds 1 step for R/W head, 
// thus, a multi-dim tensor is indexed like a flatten tensor. 
// Workers are contiguous, so tensor must be as well.
#define CHECK_CONTIGUOUS(x) TORCH_CHECK(x.is_contiguous(), #x " must be contiguous")

// Combine two conditions:
#define CHECK_INPUT(x) CHECK_CUDA(x); CHECK_CONTIGUOUS(x)

// Declear the cuda kernel
torch::Tensor trilinear_fw_cu(
    const torch::Tensor feats,
    const torch::Tensor points
);

cu

CUDA kernel: “interpolation_kernel.cu”

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

#include <torch/extension.h>

// kernel function
template <typename scalar_t>   // for type of scalar_t
__global__ void trilinear_fw_kernel(    // no return value
    // input variables are packed_accessor
    const torch::PackedTensorAccessor<scalar_t, 3, torch::RestrictPtrTraits, size_t> feats,
    const torch::PackedTensorAccessor<scalar_t, 2, torch::RestrictPtrTraits, size_t> points,
    torch::PackedTensorAccessor<scalar_t, 2, torch::RestrictPtrTraits, size_t> feat_interp
){
    // index thread along x for samples:
    const int n = blockIdx.x * blockDim.x + threadIdx.x;
    // index thread along y for features:
    const int f = blockIdx.y * blockDim.y + threadIdx.y;

    // Terminate exceeded threads without input data
    if (n >= feats.size(0) || f >= feats.size(2)) return;

    // Put results into output variable
    // normalized coordinates in each cell, [-1,1] -> [0,1]
    const scalar_t u = (points[n][0]+1)/2;
    const scalar_t v = (points[n][1]+1)/2;
    const scalar_t w = (points[n][2]+1)/2;

    // factors
    const scalar_t a = (1-v)*(1-w);
    const scalar_t b = v*(1-w);
    const scalar_t c = (1-v)*w;
    const scalar_t d = v*w;

    // Each thread will perform:
    feat_interp[n][f] = (1-u) * (a*feats[n][0][f] +
                                 b*feats[n][1][f] +
                                 c*feats[n][2][f] +
                                 d*feats[n][3][f]) +
                        u * (a*feats[n][4][f] +
                             b*feats[n][5][f] +
                             c*feats[n][6][f] +
                             d*feats[n][7][f]);
}

// foward pass
torch::Tensor trilinear_fw_cu(
    torch::Tensor feats, // (N=20, 8, F=10)
    torch::Tensor points // (N=20, 3)
){
    const int N = points.size(0);
    const int F = feats.size(2);

    // Initialize the output data residing on the same devices
    // as the input data
    torch::Tensor feat_interp=torch::empty({N,F}, feats.options());

    // Allocate threads and blocks
    // #Threads per block: 256 (Rule of thumb).
    // Threads can be 3-D (cube) at most, where each dim can be set as proportional as the data's shape.
    // Two dimensions will run in parallel: N (20) and F (10)
    const dim3 threads(16, 16, 1);  // total 256. 

    // #Blocks is determined by repeating `threads` to sufficiently cover the output data.
    const dim3 blocks( (N+threads.x-1)/threads.x, (F+threads.y-1)/threads.y );

    // Launch threads to compute for each "voxel" in the "cube" of block
    AT_DISPATCH_FLOATING_TYPES(feats.type(), "trilinear_fw_cu",
    ([&] {  // call kernel function with passing input and output
        trilinear_fw_kernel<scalar_t><<<blocks, threads>>>(
            feats.packed_accessor<scalar_t, 3, torch::RestrictPtrTraits, size_t>(),
            points.packed_accessor<scalar_t, 2, torch::RestrictPtrTraits, size_t>(),
            feat_interp.packed_accessor<scalar_t, 2, torch::RestrictPtrTraits, size_t>()
        );
    } )  );

    return feat_interp;
}

  1. Since 2 dimensions of the output tensor both require parallism, 256 threads in a block are resized to a square of (16, 16).

  2. To ensure each element of the output tensor assigned with a thread, 2 by 1 (2,1) blocks are required.

    Such that each element will be computed by a thread (“box”) individually.

2 - 0 ‖ ‖ ‖ ‖ ‖ ⋅ ‖ ‖ ‖ ‖ ‖ ‖ ' = = □ □ □ □ □ = □ □ □ □ □ = = □ □ □ □ □ = □ □ □ □ □ = = □ □ □ □ □ = □ □ □ □ □ = 1 = □ □ □ □ □ = □ □ □ □ □ = 0 = □ □ □ □ □ = □ □ □ □ □ = = □ □ □ □ □ = □ □ □ □ □ = 1 = □ □ □ □ □ = □ □ □ □ □ = 6 = □ □ □ □ □ = □ □ □ □ □ = □ □ □ = = □ □ □ □ □ = □ □ □ □ □ □ = = □ □ □ □ □ = □ □ □ □ □ □ = = □ □ □ □ □ = □ □ □ □ □ □ = . ‖ ‖ ‖ ‖ ‖ ⋅ ‖ ‖ ‖ ‖ ‖ ‖ ' 1 6 I ‖ ‖ ‖ ‖ ‖ ⋅ ‖ ‖ ‖ ‖ ‖ ‖ ' s = o = □ □ □ □ □ = □ □ ⊠ ⊠ ⊠ = l = □ □ □ □ □ = □ □ ⊠ ⊠ ⊠ = a T = □ □ □ □ □ = □ □ ⊠ ⊠ ⊠ = t h = □ □ □ □ □ = □ □ ⊠ ⊠ ⊠ = e r = □ □ □ □ □ = □ □ ⊠ ⊠ ⊠ = e = □ □ □ □ □ = □ □ ⊠ ⊠ ⊠ = 1 U a = □ □ □ □ □ = □ □ ⊠ ⊠ ⊠ = 6 n d = □ □ □ □ □ = □ □ ⊠ ⊠ ⊠ = u s ⊠ ⊠ ⊠ = s = ⊠ ⊠ ⊠ ⊠ ⊠ = ⊠ ⊠ ⊠ ⊠ ⊠ ⊠ = e = ⊠ ⊠ ⊠ ⊠ ⊠ = ⊠ ⊠ ⊠ ⊠ ⊠ ⊠ = d = ⊠ ⊠ ⊠ ⊠ ⊠ = ⊠ ⊠ ⊠ ⊠ ⊠ ⊠ = . ‖ ‖ ‖ ‖ ‖ ⋅ ‖ ‖ ‖ ‖ ‖ ‖ ' 1 6

Notes:

  1. threads and blocks are not assigned with tuples:

    1
2

    const dim3 threads = (16, 16, 1);  // total 256. 
const dim3 blocks = ( (N+threads.x-1)/threads.x, (F+threads.y-1)/threads.y )

    They’re object instantiated from classes:

    1
2

    const dim3 threads(16, 16, 1);  // total 256. 
const dim3 blocks( (N+threads.x-1)/threads.x, (F+threads.y-1)/threads.y )

  2. If multiple tensors need return, the return type of the func should be std::vector<torch::Tensor>. And the end syntax: return {feat_interp, points};

Kernel func

Source video: P4

  1. AT_DISPATCH_FLOATING_TYPES got passed data type and a name for error prompt.

  2. scalar_t is used to allow various float types of input data to kernel function trilinear_fw_kernel, as AT_DISPATCH_FLOATING_TYPES can recieve float16, float32, float64.

    • Specify sepcific dtype rather than scalar_t and size_t:

      1
2
3
4
5
6

      trilinear_fw_kernel<<blocks, threads>>(
   feats.packed_accessor<float, 3, torch::RestrictPtrTraits>(),
   points.packed_accessor<float, 2, torch::RestrictPtrTraits>(),
   feat_interp.packed_accessor<float, 2, torch::RestrictPtrTraits>(),
   var_not_tensor // packed_accessor is only for tensor
)

  3. packed_accesor indicates how to index elements by stating “datatype” (scalar_t) and “number of dimensions” (3) for each input. And size_t means shape of an index aligned with scalar_t.

  4. torch::RestrictPtrTraits: Memory is independent to any other variables.

  5. Kernel trilinear_fw_kernel doesn’t return any value (void), with directly changing the memory of output data. Thus, output must be passed.

  6. __global__ means kernel function is called on cpu and excecuted on cuda devices.

    • __host__ for functions called on cpu and run on cpu.
    • __device for functions called and run both on cuda device.

  7. Indexing samples by n and indexing features by f.

  8. If threads accessed empty area, program returns.

setup.py

Building CudaExtension: “setup.py”

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

from setuptools import setup
from torch.utils.cpp_extension import CUDAExtension, BuildExtension
from pathlib import Path

ROOT_DIR = Path.cwd()
exts = [".cpp", ".cu"]
sources = [str(p) for p in ROOT_DIR.rglob('*') if p.suffix in exts]
include_dirs = [ROOT_DIR / "include"]

setup(
    name="my_cppcuda_pkg",
    version="0.1",
    description="cppcuda example",
    long_description="cpp-cuda extension",
    author="z",
    author_email="luckily1640@gmail.com",
    ext_modules=[
        CUDAExtension(
            name='my_cppcuda_pkg', 
            sources=sources, # code files
            include_dirs=include_dirs,
            extra_compile_args={'cxx': ['-O2'],
                                'nvcc': ['-O2']}
            ) 
    ],
    cmdclass={  # commands to be executed
        "build_ext":BuildExtension
        } 
)
  • Build and install: pip install .
  • Delete failed building history manually: “/home/yi/anaconda3/envs/AIkui/lib/python3.10/site-packages/my_cppcuda_pkg-0.1.dist-info”

test.py

Python function: “test.py”

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

import torch
from my_cppcuda_pkg import trilinear_interpolate

N = 65536; F = 256

feats = torch.rand(N,3, F, device='cuda')
points = torch.rand(N,3, device='cuda')*2-1   # [0,1] -> [-1,1]

out = trilinear_interpolate(feats, points)
print(out.shape)

title: “watch: CppExt - AI葵 05 | Validate” date: 2023-10-28T12:05:00

To validate if cuda kernel yields correct results, impelement a PyTorch version.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

import torch
import my_cppcuda_pkg
import time

def trilinear_interpolate_py(feats, points):
    r"""
    feats: (N, 8, F), features on 8 vertices
    points: (N, 3) , coordinates [-1,1]
    """

    u,v,w = (points[:,0:1]+1)/2, (points[:,1:2]+1)/2, (points[:,2:3]+1)/2

    a,b,c,d = (1-v)*(1-w), v*(1-w), (1-v)*w, v*w

    feat_interp = (1-u) * (a*feats[:,0] + b*feats[:,1] + c*feats[:,2] + d*feats[:,3]) \
                 + u*(a*feats[:,4] + b*feats[:,5] + c*feats[:,6] + d*feats[:,7])

    return feat_interp  # (N,F)

if __name__ == "__main__":
    N=65536; F=256
    feats = torch.rand(N,8,F, device="cuda").requires_grad_(True)
    points = torch.rand(N,F, device="cuda")*2-1

    t = time.time()
    out_cuda = my_cppcuda_pkg.trilinear_interpolate(feats, points)
    torch.cuda.synchronize()
    print(f'CUDA time: {time.time()-t} s')

    t = time.time()
    out_py = trilinear_interpolate_py(feats, points)
    torch.cuda.synchronize()
    print(f'PyTorch time: {time.time()-t} s')

    print(f"fw all close? {torch.allclose(out_cuda, out_py)}")
    print(f"Cuda has grad? {out_cuda.requires_grad}")

title: “watch: CppExt - AI葵 06 | Backward” date: 2023-10-28T16:40:00

Source video: Pytorch+cpp/cuda extension 教學 tutorial 6 反向傳播 - English CC -

Compute Partial Derivatives

When loss L comes, the partial derivatives of L w.r.t. every trainable input variable of the function are required.

Trilinear interpolation:

$$ \begin{aligned} f(u,v,w) = (1-u) * [ & (1-v)(1-w)f₁ + v(1-w)f₃ + (1-v)wf₅ + vw f₇ ] \\ + u * [ & (1-v)(1-w)f₂ + v(1-w)f₄ + (1-v)w f₆ + vwf₈ ] \end{aligned} $$

  1. u,v,w are coordinates, which are constant (requires_grad is False). So only vertices features f₁, f₃, f₅, f₇, f₂, f₄, f₆, f₈ need optimizing.

  2. Given interpolated result f, their gradients for this operation are:

    $$ \begin{aligned} &\frac{∂f}{∂f₁} = (1-u)(1-v)(1-w); &\frac{∂f}{∂f₂} &= u(1-v)(1-w); \\ &\frac{∂f}{∂f₃} = (1-u)v(1-w); &\frac{∂f}{∂f₄} &= uv(1-w); \\ &\frac{∂f}{∂f₅} = (1-u)(1-v)w; &\frac{∂f}{∂f₆} &= u(1-v)w; \\ &\frac{∂f}{∂f₇} = (1-u)vw &\frac{∂f}{∂f₈} &= uvw \end{aligned} $$

  3. The derivatives of L w.r.t. features f₁, f₂, f₃, f₄, f₅, f₆, f₇, f₈ are:

    $$ \frac{∂L}{∂f} \frac{∂f}{∂f₁}; \quad \frac{∂L}{∂f} \frac{∂f}{∂f₂}; \quad \frac{∂L}{∂f} \frac{∂f}{∂f₃}; \quad \frac{∂L}{∂f} \frac{∂f}{∂f₄}; \quad \frac{∂L}{∂f} \frac{∂f}{∂f₅}; \quad \frac{∂L}{∂f} \frac{∂f}{∂f₆}; \quad \frac{∂L}{∂f} \frac{∂f}{∂f₇}; \quad \frac{∂L}{∂f} \frac{∂f}{∂f₈} $$

Bw Kernel

  1. Write host function trilinear_bw_cu based on trilinear_fw_cu in “interpolation_kernel.cu”

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

    torch::Tensor trilinear_bw_cu(
    const torch::Tensor dL_dfeat_interp,  // Inputs
    const torch::Tensor feats,
    const torch::Tensor points
){
    const int N = points.size(0);
    const int F = feats.size(2);
    torch::Tensor dL_dfeats=torch::empty({N,8,F}, feats.options()); // output data
    const dim3 threads(16,16);
    const dim3 blocks((N+threads.x-1)/threads.x, (F+threads.y-1)/threads.y);

    // Launch kernel function
    AT_DISPATCH_FLOATING_TYPES(feats.type(), "trilinear_bw_cu",
    ([&] {
        trilinear_bw_kernel<scalar_t><<<blocks, threads>>>(
            dL_dfeat_interp.packed_accessor<scalar_t, 2, torch::RestrictPtrTraits, size_t>(),
            feats.packed_accessor<scalar_t, 3, torch::RestrictPtrTraits, size_t>(),
            points.packed_accessor<scalar_t, 2, torch::RestrictPtrTraits, size_t>(),
            dL_dfeats.packed_accessor<scalar_t, 3, torch::RestrictPtrTraits, size_t>() );
         }
    )
    );
    return dL_dfeats;
}

  2. Write kernel function trilinear_bw_kernel based on trilinear_fw_kernel in “interpolation_kernel.cu”:

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

    template <typename scalar_t>
__global__ void trilinear_bw_kernel(
    const torch::PackedTensorAccessor<scalar_t, 2, torch::RestrictPtrTraits, size_t> dL_dfeat_interp,
    const torch::PackedTensorAccessor<scalar_t, 3, torch::RestrictPtrTraits, size_t> feats,
    const torch::PackedTensorAccessor<scalar_t, 2, torch::RestrictPtrTraits, size_t> points,
    torch::PackedTensorAccessor<scalar_t, 3, torch::RestrictPtrTraits, size_t> dL_dfeats
){
    const int n = blockIdx.x * blockDim.x + threadIdx.x;
    const int f = blockIdx.y * blockDim.y + threadIdx.y;

    if (n >= points.size(0) || f>= feats.size(2)) return;

    // Define helper variables
    const scalar_t u = (points[n][0]+1)/2;
    const scalar_t v = (points[n][1]+1)/2;
    const scalar_t w = (points[n][2]+1)/2;
    const scalar_t a = (1-v)*(1-w);
    const scalar_t b = v*(1-w);
    const scalar_t c = (1-v)*w;
    const scalar_t d = v*w;

    // Compute derivatives
    dL_dfeats[n][0][f] = dL_dfeat_interp[n][f]*(1-u)*a;
    dL_dfeats[n][1][f] = dL_dfeat_interp[n][f]*(1-u)*b;
    dL_dfeats[n][2][f] = dL_dfeat_interp[n][f]*(1-u)*c;
    dL_dfeats[n][3][f] = dL_dfeat_interp[n][f]*(1-u)*d;
    dL_dfeats[n][4][f] = dL_dfeat_interp[n][f]*u*a;
    dL_dfeats[n][5][f] = dL_dfeat_interp[n][f]*u*b;
    dL_dfeats[n][6][f] = dL_dfeat_interp[n][f]*u*c;
    dL_dfeats[n][7][f] = dL_dfeat_interp[n][f]*u*d;
}

  3. Add the function signature into header file “include/utils.h”

    1
2
3
4
5

    torch::Tensor trilinear_bw_cu(
    const torch::Tensor dL_dfeat_interp,
    const torch::Tensor feats,
    const torch::Tensor points
);

  4. Add a cpp function to call the backward method trilinear_bw_cu in “interpolation.cpp”:

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

    torch::Tensor trilinear_interpolate_bw(
    const torch::Tensor dL_dfeat_interp,
    const torch::Tensor feats,
    const torch::Tensor points
){
    CHECK_INPUT(dL_dfeat_interp);
    CHECK_INPUT(feats);
    CHECK_INPUT(points);

    return trilinear_bw_cu(dL_dfeat_interp, feats, points);
}

    Give the function trilinear_interpolate_bw a name in PYBIND as a method of the package:

    1
2
3
4

    PYBIND11_MODULE(TORCH_EXTENSION_NAME, m){
    m.def("trilinear_interpolate", &trilinear_interpolate);
    m.def("trilinear_interpolate_bw", &trilinear_interpolate_bw);
}

Encapsulate

Wrap forward and backward by a subclass inherited from torch.autograd.Function in “test.py”:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class trilinear_interpolate_cuda(torch.autograd.Function):
    @staticmethod
    def forward(ctx, feats, points):
        feat_interp = my_cppcuda_pkg.trilinear_interpolate(feats, points)
        ctx.save_for_backward(feats, points)
        return feat_interp

    @staticmethod
    def backward(ctx, dL_dfeat_interp): 
    # The number of input vars corresponds to return values of forward pass.
    # i.e., inputs are gradients of Loss w.r.t the forward's outcomes.
        feats, points = ctx.saved_tensors

        dL_dfeats = my_cppcuda_pkg.trilinear_interpolate_bw(
            dL_dfeat_interp.contiguous(), feats, points)
        return dL_dfeats, None  # return gradients of Loss w.r.t each input data forward

Notes:

  1. The nubmer of return values needs to match the input to forward pass. If some input doesn’t require grad, return a None.

  2. ctx is mandatory for storing intermeidate data.

Verify Graident

Test the gradient of backward:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

# test.py
import torch
import my_cppcuda_pkg
import time

def trilinear_interpolate_py(feats, points):
    r"""
    feats: (N, 8, F), features on 8 vertices
    points: (N, 3) , coordinates [-1,1]
    """

    u,v,w = (points[:,0:1]+1)/2, (points[:,1:2]+1)/2, (points[:,2:3]+1)/2

    a,b,c,d = (1-v)*(1-w), v*(1-w), (1-v)*w, v*w

    feat_interp = (1-u) * (a*feats[:,0] + b*feats[:,1] + c*feats[:,2] + d*feats[:,3]) \
                 + u*(a*feats[:,4] + b*feats[:,5] + c*feats[:,6] + d*feats[:,7])

    return feat_interp  # (N,F)


if __name__=="__main__":
    N = 1024; F=256
    feats = torch.rand(N,8,F, device="cuda")
    feats_py = feats.clone().requires_grad_()
    feats_cu = feats.clone().requires_grad_()
    points = torch.rand(N,3, device="cuda")*2-1

    t = time.time()
    out_py = trilinear_interpolate_py(feats_py, points)
    torch.cuda.synchronize()
    print(f"py: {time.time() - t}")

    t = time.time()
    out_cuda = trilinear_interpolate_cuda.apply(feats_cu, points)
    torch.cuda.synchronize()
    print(f"cu: {time.time() - t}")

    loss_py = out_py.sum()
    loss_cuda = out_cuda.sum()

    loss_py.backward()
    loss_cuda.backward()

    print(f"Grad all close? {torch.allclose(feats_py.grad, feats_cu.grad)}")