memo: PyTorch | Autograd

Elliot Waite

Source video: PyTorch Autograd Explained - In-depth Tutorial-Elliot Waite

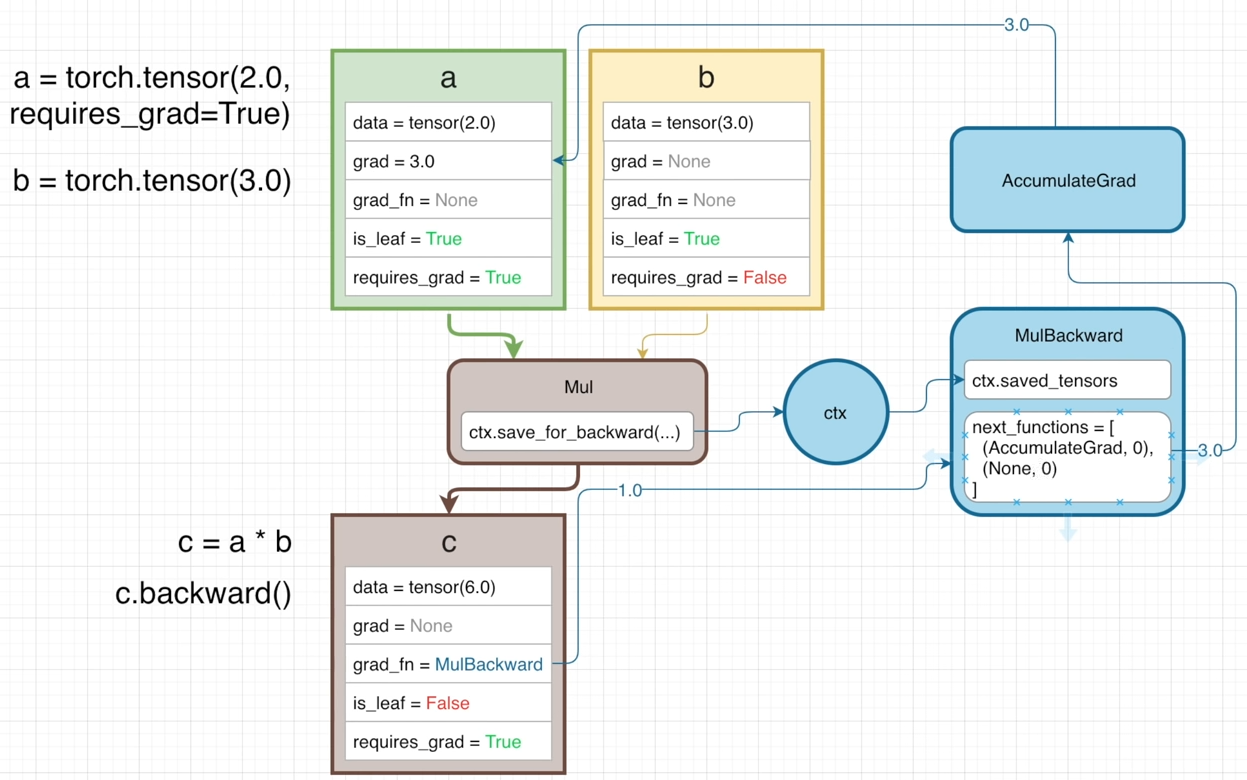
Two tensors are created with the values of 2 and 3 and assigned to variables a and b. Then the product of a and b is assigned to variable c.

In the following diagram, each struct is a tensor containing several attributes.

  • data holds the data of the tensor
  • grad holds the calculated gradient value
  • grad_fn, gradient function points to a node in the backwards graph
  • is_leaf marks is this tensor a leaf of a graph
  • requires_grad is False by default for all tensors that are being input (like a,b) into or output (like c) from an operation. Such that no backwards graph will be created.

However, if the attribute requires_grad of a is set to True and a is passed into any operation (Mul), the output tensor (c) will also have requires_grad=True and be apart of the backwards graph, because c is no longer a leaf.
And c’s grad_fn points to MulBackward, which calculates the gardient of its operation w.r.t. input tensor a: ∂c/∂a = ∂(a∗b)/∂a = b

The blue contents are the backwards graph behind the tensors and their operations.

  • When the Mul function is called, the ctx context variable will save the values to be used in the backwards pass: MulBackward operation.

  • Specifically, the input tensor a is stored by the method ctx.save_for_backward(...) and referenced by the property ctx.saved_tensors in the backward pass.

  • The MulBackward has another attribute next_functions is a list of tuples, each one associated with an input tensor that were passed to the Mul operation.

    • (AccumulatedGrad, 0) corresponds to the input tensor a meaning the gradient of a will be calculated continuously by AccumulatedGrad operation.
    • (None, 0) is associated with input tensor b, no further calculation is needed for its gradient.

  • The AccumulateGrad operation is used to sum the gradients (from multiple operations) for the input tensor a.

When executing c.backward(), the backward pass of gradients starts. The initial gradient is 1.0 and then passed into MulBackward, where it times b getting 3.0. Then by looking at the next_functions, it needs to get into AccumulatedGrad to obtain the gradient w.r.t. tensor a. Finally, the attribute grad of a comes from AccumulateGrad.

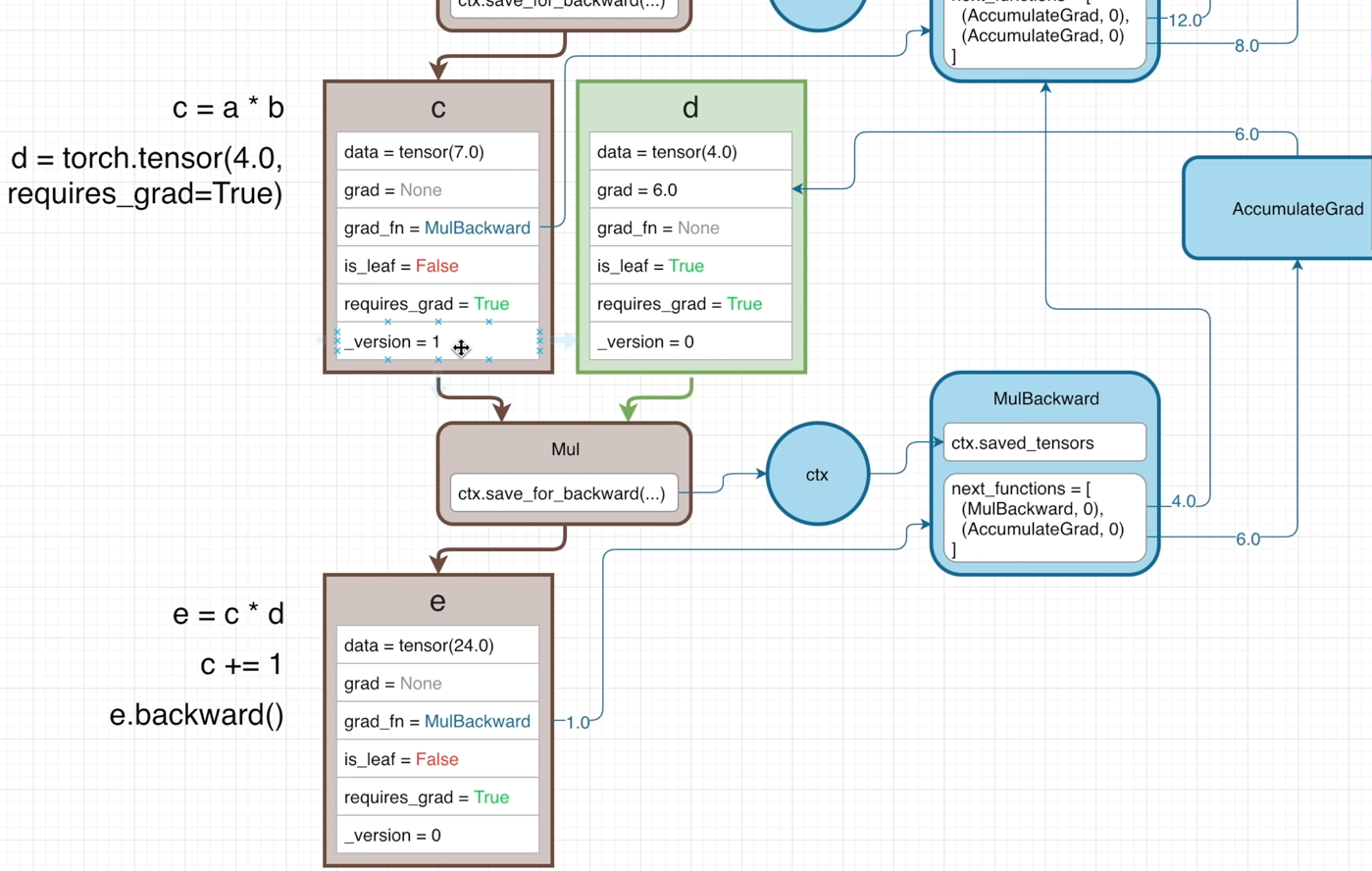
Simple example

Two input tensors are both requires_grad=True.

They’re multiplied together to get c.

If here executing c.backward(), the initial gradient 1.0 will start the backward pass from its grad_fn.

Then tensor d is created to multiply with c to get e.

If executing e.backward() here, to calculate the gradient of e w.r.t. the leaft nodes on the graph, the backward pass is as follows:

  • The initial gradient 1.0 is first passed into e.grad_fn, i.e., MulBackward, where it multiplies with gradient of the operation w.r.t. the leaf nodes: ∂(c∗d)/∂d (=c=6.0).
    (Since c is not a leaf, ∂e/∂c doesn’t need to compute.)

  • Then by looking at property next_functions, the gradients go continuously into MulBackward and AccumulateGrad separately.

    • In MulBackward, to get ∂e/∂a, the incoming gradient ∂e/∂c multiplies with gradient of the Mul operation w.r.t. a: ∂(a∗b)/∂a, so the gradient of leaf a is ∂e/∂a = ∂e/∂c × ∂(a∗b)/∂a = 4×3=12.
      Also to get ∂e/∂b, the incoming gradient ∂e/∂c multiplies with ∂(a∗b)/∂b, ∂e/∂b = ∂e/∂c × ∂(a∗b)/∂b = 4×2 = 8
    • While ∂e/∂c gets into AccumulateGrad, no other operations needed to calculate the gradients w.r.t. d, the grad of leaf node d is 6.0.

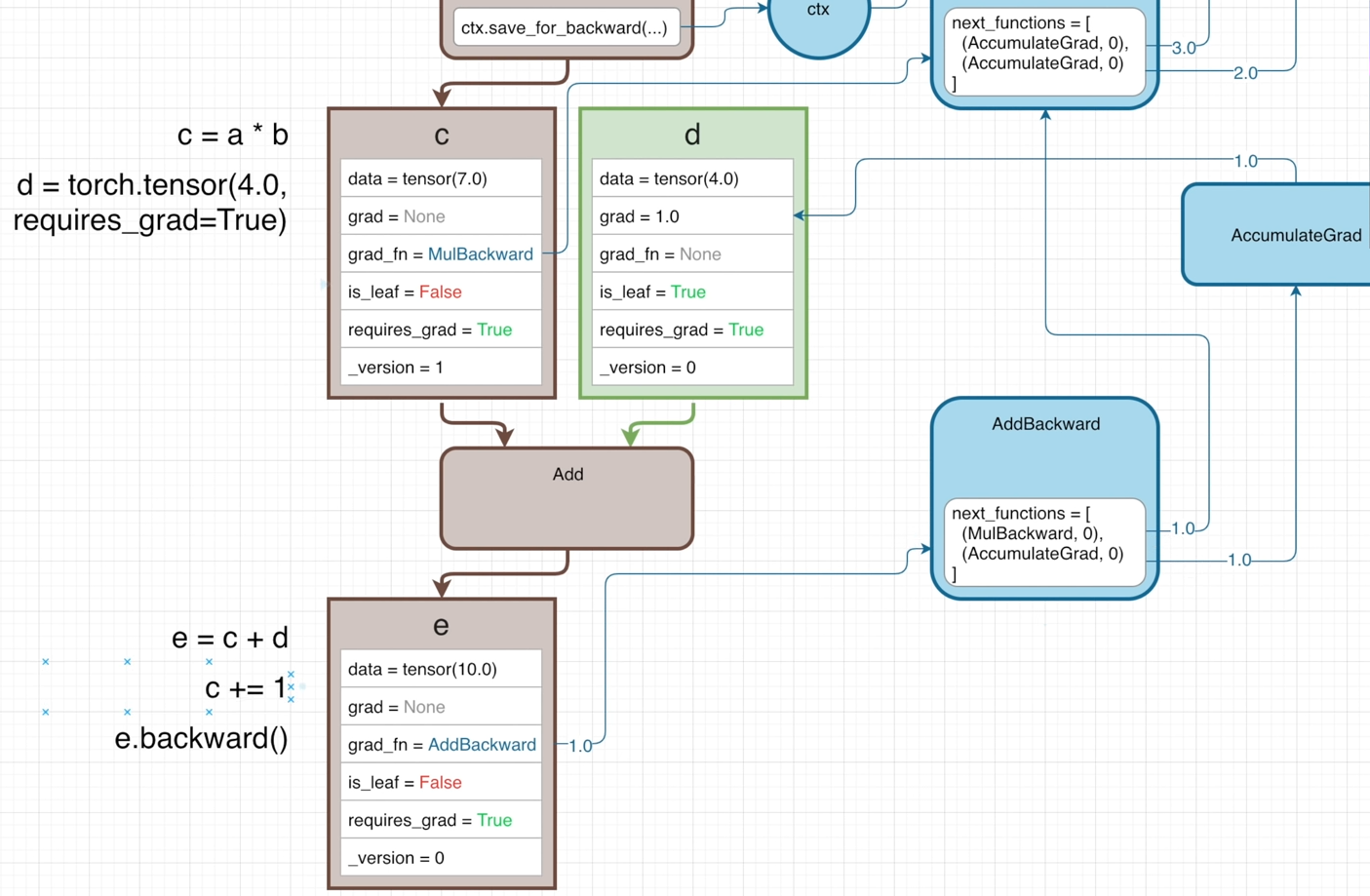
Avoid In-place operation

When the MulBackward operation retrieve input tensors through ctx.saved_tensors, it is necessary to ensure that the correct values are referenced. Therefore, each tensor must maintains its attribute _version, which will be increamented (+1) when performing in-place operation (e.g., c+=1) each time.

Thus, if calling e.backward() after c+=1, the ctx.saved_tensors will get an error, beacuse the attribute _version of the input tensor c is not matched with the previously saved one. In this way, the input tensors to be used are ensured haven’t changed in the time since the operation was performed in the forward pass.

However, the Add function doesn’t affect the graidents, so it doesn’t need to save any its input tensors for the backward pass. Hence, the ctx will not store its input tensors. And the initial gradient will directly looking at the next_functions after getting into AddBackward node. In this case, doing c+=1 before e.backward(), no errors will occur because the input tensor c is not retrieved by ctx.saved_tensors.

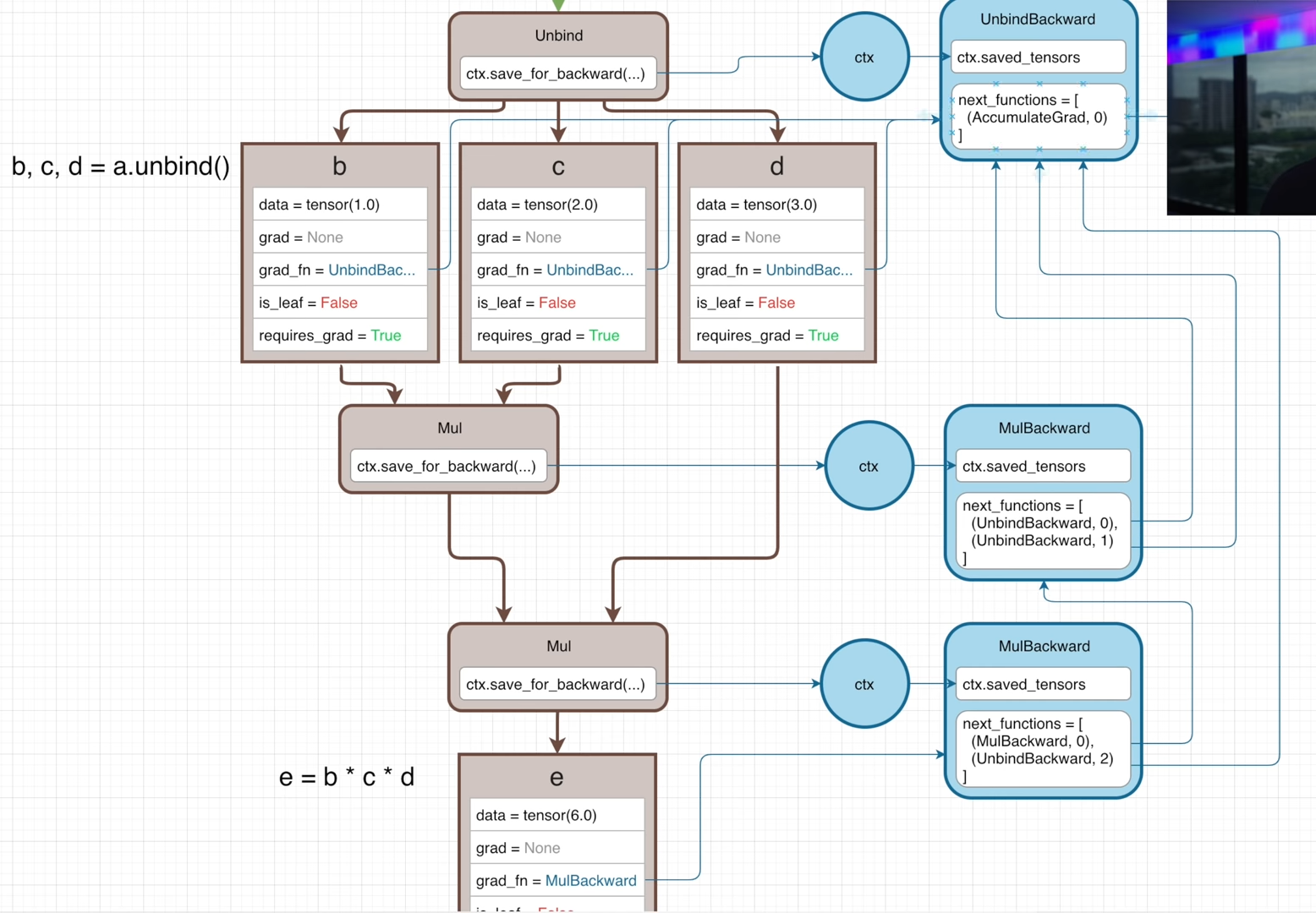
Unbind operation

A tensor is created with 1-D list holding 3 values and assigned to variable a.

Then by executing b,c,d = a.unbind(), tensor a is split along the 1st dimension and tensors b, c, d are created. This operation will generate the graph as follows:

All of the grad_fn of b, c, d point to the same UnbindBackward function.

If b, c, d are multiplied together to get e, there will be two Mul operation in the forward pass and two MulBackward is the backward pass.

The property next_functions of those 2 MulBackward functions both have tuple (UnbindBackward, i ), but their indecies are different, where i is 0, 1, 2 corresponding to the 3 outputs from the Unbind function.

  • (UnbindBackward, 0) means the current gradient is associated with the first input tensor b of the (1st) Mul operation, which is also the first output from the Unbind function.
  • (UnbindBackward, 1) is saying this is the gradient for the second output fromt he Unbind function.
  • (UnbindBackward, 2) indicates this gradient is for the third output of the Unbind function.

The index value is used to inform the UnbindBackward which output tensor the gradient is calculated for. Such that the UnbindBackward can output a list of gradients.

The gradient of the leat node can be calculated by calling e.backward(). The backward pass is started off with the initial gradient of 1.

Complicated example

The following scalar tensor can be replaced with any vector or matrix or any n-dimension array.

The tensors are created with the same value of 2 and they both don’t require grad.

a and b are multiplied together to get c, which doesn’t require grad too.

Then by executing c.requires_grad = True, the tensor c will be a port of the backwards graph. So that any future operations done using c as an input will start to build the backwards graph.

The full forward graph is build as:

  • Another tensor d is created with requires_grad=False.
  • Multiply d with c to get e.
  • Another leaf f is constructed with requires_grad=False (not on the graph).
  • Multiply f with e to get g
  • Another tensor h is created with requires_grad=True (a leaf on the graph).
  • Devide g by h to get i;
  • Add i and h together to get j. (h is leaf and fed into 2 operations, so its AccumulteGrad has two inputs from DivBackward and AddBackward.
  • Multiply j and i together to get k. (i is passed into both Add and Mul, so its (grad_fn) DivBackward has 2 streams from AddBackward and MulBackward.
    Unlike h has its 2 backward streams converge at AccumulateGrad, the 2 backward streams of i instead converge at the DivBackward that corresponds to the operation Div generating the i.

(Yellow means the leaf that doesn’t on the graph. Green means the leaf on the graph. Brown means the non-leaf)

At the end, by executing k.backward(), the backward pass will start with a gradient of 1.0, which will times the gradient of each operation w.r.t. local input tensors sequentially from bottom to top. If an operation’s input is a leaf, the next_functions will point to the AccumulateGrad for this leaf node. Once all gradients streams are accumulated, the sum is put into the attribute grad of the left node. Finally, ∂k/∂leaf will obtained.

retain_grad()

By default, the gradients will only calculated for the leaf nodes, and the grad of the intermediate nodes are kept None. But an intermediate tensor can retain their gradient by calling its retain_grad() method. For example, i.retain_grad(), which will set up a hook “that gets called in the backward pass that will basically tell the DivBackward function that any gradients passed into it should be saved on the grad attribute of tensor i.

detach()

m = k.detach() will create a new tensor sharing the same underlying data as k, but m will no longer require gradients. m will be a leaft node but not on the graph because its grad_fn is None without pointing any node on the graph.

Usually, the backwards graph is expected to get garbage collected after finishing the training loop. Once the k.backward() is executed, some values have no references (get freed) in the graph. Specifically, the references to the saved_tensors. But the actual graph still exists in memory. If the output tensor k is needed to kept for longer than the training loop, k can be detached from the graph.

Similar functions:

  • k.numpy() : ndarray
  • k.item() : python int or python float
  • k.tolist() : original tensor that holds multiple values will be converted to python list

(old summary on 2022-10-19)

Those tensors whose attribute requires_grad=True will be nodes on a backwards graph. Any output tensor yielded from any operation is not leaf node.

grad_fn & grad

The grad_fn of the ’non-leaf’ (intermediate) node points to a node (like MulBackward) which will multiply the incoming gradient by the gradient of this operation w.r.t. its inputs (leaf nodes with requires_grad=True), or pass the grad of the ’non-leaf’ node up to next gradient-computing node for other leaf nodes before. This’s like the divergence of ∂L/∂wᶦ and ∂L/∂wᶦ⁻¹.

If an “non-leaf” node is passed into multiple operations, its gradient equals the sum of the gradients coming from each operation. Its gradient will be fed into the “gradient-computing” node as the incoming gradient of the operation that generates it.

While if a leaf node is used by multiple functions, its gradient equals to the sum of the gradients comeing from the “gradient-computeing” nodes of every operation. Hence, the grad of the leaf node is accumulated by AccumulateGrad function.

ctx

ctx (context) stores the operators doing the operation for computing the gradient in backward graph. The gradients at different time are different, so the version of variables needs to be recorded. The in-place operation will increment the version of the variable, and then calling the backward method will cause an error due the mismatch of the _version value.

However, if an operation doesn’t bring gradients (like Add), its operators are not necessary to store. The incoming gradient will not change when passing through its corresponding backwards function (AddBackward). In this case, modifying its operators before calling .backward() is okay, becaue they are not involved with gradient.

Gradient for a one-dim tensor is a list of partial derivative. The second value in the tuple is the index among the mutliple outputs of the operation, indicating to who the gradient belongs

output don’t have grad by default

The “non-leaf” node will not store grad by default, unless set its .retain_grad(), from which a hook can be set up to make its grad_fn to save any gradient passed to it into grad of this node.

detach()

m=k.detach() will create a leaf node m sharing the same data as k, but will no longer require gradient. Its grad_fn=None meaning it doesn’t have a reference to the backwards graph. This operation is used to store a output value separately, but free the backwards graph after a training loop (forward+backward). Alternatives for detaching from the graph:

  1. k.numpy(),
  2. k.item() convert one-element tensor to python scalar.
  3. k.tolist().

(2022-11-01)

  • gradient is the upstream gradients until this calling tensor (from the intermediate node to the network ouput).
    Since the explicit expression of output is unknown, the derivative $\rm\frac{ d(output) }{ d(input) }$ cannot be calculated directly. But the derivative $\rm\frac{ d(output) }{ d(intermediate) }$ and $\rm\frac{ d(intermediate) }{ d(input) }$ are all known. Therefore, by passing the d(output)/d(intermediate), say 0.05, to gradient, the d(output)/d(input) is the returned value of intermeidate.backward(gradient=0.05,). The gradient argument in PyTorch backward - devpranjal Blog

(2023-08-02)

Freeze params

  1. module.requires_grad_(False) will change all its parameters. PyTorch Forum

    • If I explicitly add the learnable params one-by-one, like this tutorial (if p.requires_grad), only the ordinal of the layers in the state dict ckpt['optimizer]['state'] changed, while the total number of states remains the number of layers to be performing gradient descent.

      1
2
3
4
5
6
7

      # Test in GNT with multiple encoders:
self.optimizer.add_param_group({"params": self.multiEncoders.parameters()})
# Saved `ckpt['optimizer']['state']` has a max index: 1390, but total 262 layers.

params = [p for p in self.multiEncoders.parameters() if p.requires_grad]
self.optimizer.add_param_group({"params": params})
#`ckpt['optimizer']['state']` has a max index: 281, but total 262 layers too.

  2. with torch.no_grad(): will stop backward-propagation for a block of operations wrapped in its region (in a context). This is equivalent to module.requires_grad_(False). Demo-SO

    • Inference mode is similar with no_grad, but even faster.

  3. module.eval() = module.train(False) affects the settings of nn.Dropout and nn.BatchNorm2d. And it has nothing to do with grad. Docs - Autograd

    • In pixelNeRF, self.net.eval() and self.net.train() will jump to SwinTransformer2D_Adapter.train(mode=True)

requires_grad_ vs requires_grad

requires_grad_ can do for non-leaf node, while requires_grad will have error. PyTorch Forum

Twice nn.Parameter

(2024-04-11)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

import torch
from torch import nn
from torchviz import make_dot
x = torch.rand(2,3)
w = torch.rand(3,2).requires_grad_(True)
for i in range(2):
    f = nn.Parameter(w @ x) # shape (3,3)
    loss = f.sum()
    loss.backward()

    # dot = make_dot(loss, params={'w': w, 'x': x})
    # dot.render('computational_graph', format='png')

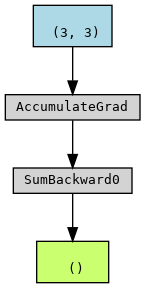
As shown above, once “re-convert” the w@x as the nn.Parameter, the forward graph doesn’t include w and the operation Matrixmultiplication. The graph is starting from f instead.

Therefore, even though w is a leaf node and require_grad is True, it won’t obtain .grad: w.grad is None.

In contrast, do not re-set the nn.Parameter won’t change the leaf tensors.

1
2
3
4
5
6
7

import torch
x = torch.rand(2,3)
w = torch.rand(3,2).requires_grad_(True)
for i in range(2):
    f = w @ x
    loss = f.sum()
    loss.backward()

In this way, the leaf tensors are prepared outside the for loop (specifally forward()). And the leaf tensors (i.e., w) will be added onto the graph correctly during each iteration rebuilding.

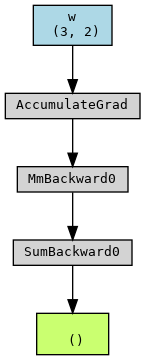
Graph in For Loop

(2024-04-11)

The computational graph (of PyTorch 1.x) is build in each iteration, as the previous graph has been destroyed after executing .backward()

Therefore, the tensors to be optimized, i.e., the leaf node of the graph, have to be present within the for loop as the starting point of the graph.

In the following code, w needs to be optimized.

1
2
3
4
5
6
7
8
9

import torch
x = torch.rand(2,3)
w = torch.rand(2,3).requires_grad_(True)
optimizer = torch.optim.Adam([w], lr=0.0001)
for i in range(2):
    f = w * x
    loss = f.sum()
    loss.backward()
    optimizer.step()

The forward graph can be plotted as:

  • The endpoint (green box) is the tensor loss
  • The w has performed Multiplication and Sum to get loss
  • The graph will be rebuilt in each iteration, with the w and x as the starting points. And the graph will be freed after loss.backward()
  • optimizer.step() updates leaf tensors that require grad. Docs
Code 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

import torch
from torchviz import make_dot
x = torch.rand(2,3)
w = torch.rand(2,3).requires_grad_(True)
optimizer = torch.optim.Adam([w], lr=0.0001)
for i in range(2):
    f = w * x
    loss = f.sum()
    loss.backward()
    optimizer.step()

    if i == 0:
        dot = make_dot(loss, params={'w': w, 'x': x})
        dot.render('computational_graph', format='png')

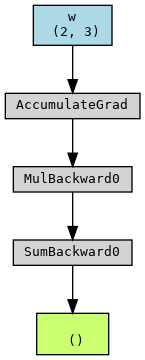
However, if moving the operation f=w*x outside the for loop, the graph only contain an operation: f.sum()

1
2
3
4
5
6
7

import torch
x = torch.rand(2)   # leaf
w = torch.rand(2).requires_grad_(True) # leaf
f = w * x   # non-leaf tensor won't have .grad
for i in range(5):
    loss = f.sum()
    loss.backward()

From the second run, the rebuilt graph only includes “Sum”, and no longer includes w (out of this graph). In other words, the w doesn’t belong to this newly rebuilt graph.

Therefore, the .backward() method cannot be completed for w.

w ∗ x = f r f e o b w u a i r f l d o d ( r ) t l h o e o p g r l a o p s h s e a c h i t e r

In the second iteration, the graph doesn’t include w. So, when the gradient backpropagates, the gradient cannot reach w.

On the other hand, the w still points to the previous graph, without updating.

Error:

1
2
3
4
5
6
7

  File "/home/yi/Downloads/CppCudaExt_PT_Tut_AIkui/test_debug.py", line 8, in <module>
    loss.backward()
RuntimeError: Trying to backward through the graph a second time 
(or directly access saved tensors after they have already been freed). 
Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). 
Specify retain_graph=True if you need to backward through the graph a second time 
or if you need to access saved tensors after calling backward.