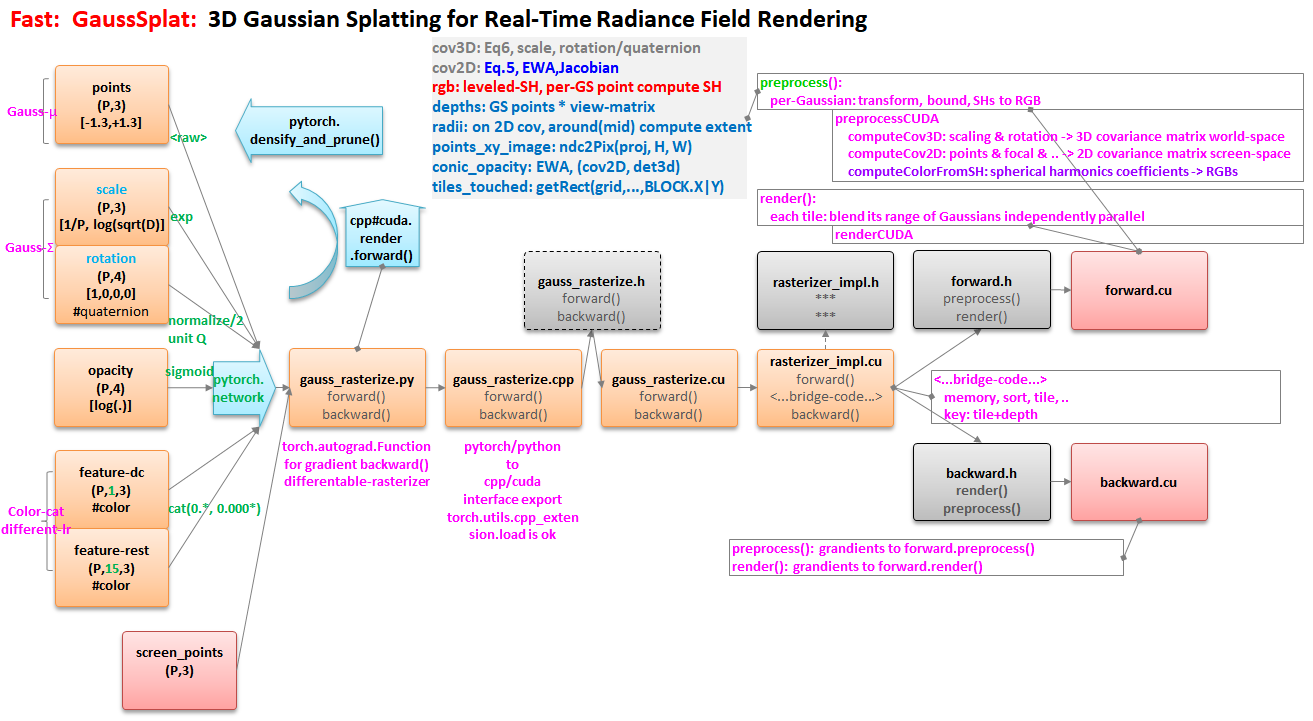
(Feature image credits: GS big picture, please say thanks to GS.#419 - yuedajiong)

gaussian-splatting python

Source code

Define Params

(2024-01-22)

1. Create PyTorch tensors for Gaussians’ parameters at GaussianModel() by __init__ them with torch.empty(0):

   • _xyz (Gaussian center), _features_dc and _features_rest (SH coeffs), _scaling (vec3), _rotation(quaternion), sh_degree (color), _opacity (unweighted alpha)

   • Each covariance matrix 𝚺 is built from a scaling vector and a quaternion:

     symm is [Σ₀₀, Σ₀₁, Σ₀₂, Σ₁₁, Σ₁₂, Σ₂₂]

2. Read point cloud and cameras at Scene() by calling __init__

   • SceneInfo:

     • Basic point cloud: points(x,y,z), normals (nx,ny,nz), colors (r,g,b)

     • CameraInfo: extrinsics (R,T), fov (FovX,FovY), gt images (image, image_name, image_path, width, height)

     • nerf_normalization (avg_cam_center (translate), max displacement from the avg cam (radius)),

   • Cameras list train_cameras of 300 Camera() is made up by repeatly loadCam()

     • Resize GT image for each camera (i.e., 300 views).

     • Viewing transform (world➡camera): self.world_view_transform

     • Projection matrix (camera➡clip): self.projection_matrix

       $$ 𝐏 = \begin{bmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & \frac{f}{f-n} & \frac{-fn}{f-n} \\ 0 & 0 & 1 & 0 \end{bmatrix} $$

       By denoting sight width as $W$, the above $r=\frac{W}{2},\ l=-\frac{W}{2}$, so $(r-l)=W$. The sight center (principle center) (cx,cy) is (r,l), i.e., (W/2, H/2) The clip coordinate of $x$ produced by multiplying 𝐏 will result in $x_{NDC} ∈ [-1,1]$

       By using this 𝐏, the final $z$ axis of ND coordinate ranges in [0,1], unlike the usual NDC cube of [-1,1]

       $$ near_{NDC} = \frac{ \frac{f * near}{f-n} + \frac{-fn}{f-n} }{n} = 0 \\ far_{NDC} = \frac{ \frac{f*far}{f-n} + \frac{-fn}{f-n} }{f} = 1 $$

       Therefore, this 𝐏 leads to a cuboid NDC space, rather than a cube NDC space. Figuratively, in the clip space, the points satisfying $0<z_{clip} < w_{clip}$ and $-w_{clip} < x_{clip}, y_{clip} < w_{clip}$ will be excluded from rendering. After clipping those point, the remaining space is the NDC space.

     • The transformation from world to clip space (P@w2c)ᵀ for each camera: self.full_proj_transform

   • Initialize Gaussians’ parameters create_from_pcd

     • _xyz is set as the basic piont cloud
     • _features_dc and _features_rest are converted from the color of the basic point cloud. The 0th-order SH coeffs is the rgb. And the rest of coeffs are initialized as 0.
     • spatial_lr_scale is set to the max displacement from the avg cam center.
     • _scaling is initialized with simple_KNN.
     • _rotation is preset with 0 and 1
     • _opacity is initilized as the inverse of sigmoid(0.1)

3. Training optimization settings, gaussians.training_setup()

   • lr for each parameter

Render

(2024-01-23)

render()

1. screenspace_points: Gaussian centers on the 2D screen are initialized as 0.

diff_gauss_raster

(2023-11-18)

Code | Explaination: kwea123/gaussian_splatting_notes

Python Invokes

1. The Python program gaussian_renderer/__init__.py calls GaussianRasterizer.forward() to render an image tile-by-tile.

2. Internally, program goes to the submodule’s _RasterizeGaussians.forward() in __ini__.py, analogous to the “test.py” that calls the cuda-extension package’s methods, which are wrapped in PyTorch’s forward and backward.

   • _C is a class of the diff_gaussian_rasterization package, as set in setup.py

   • The names of package’s methods are set in PYBIND11_MODULE()

forward Steps

1. RasterizeGaussiansCUDA() in rasterize_points.cu

   • Define geomBuffer, binningBuffer, and imgBuffer for storing data of point cloud, tiles, and the rendered image. Their memory will be allocated through a Lambda function resizeFunctional(), where tensor’s resize_ method is called.

2. ➔ CudaRasterizer::Rasterizer::forward() in cuda_rasterizer/rasterizer_impl.cu

3. ➔ FORWARD::preprocess() in cuda_rasterizer/forward.cu

4. ➔ preprocessCUDA() in forward.cu

\begin{algorithm}
\begin{algorithmic}
\STATE RasterizeGaussiansCUDA
\STATE $\quad$ CudaRasterizer::Rasterizer::forward
\STATE $\qquad$ geomState, imgState
\COMMENT{Allocate memory}
\STATE $\qquad$ FORWARD::preprocess
\STATE $\qquad$ cub::DeviceScan::InclusiveSum
\COMMENT{Count tiles}
\STATE $\qquad$ binningState
\STATE $\qquad$ duplicateWithKeys
\STATE $\qquad$ getHigherMsb
\STATE $\qquad$ cub::DeviceRadixSort::SortPairs
\STATE $\qquad$ identifyTileRanges
\STATE $\qquad$ FORWARD::render
\end{algorithmic}
\end{algorithm}

preprocessCUDA

1. Frustum culling

   Delete points whose w (equal to depth) is larger than x, y, z in clip space. However, in_frustum() is based on coordinates in the camera space.

2. Construct 3D covariance matrix. Code

   Given a quaternion $q = [r, \ x, \ y, \ z]$, the rotation matrix is: wiki

   $$ 𝐑 = \begin{bmatrix} 1 - 2(y² + z²) & 2(xy - rz) & 2(xz + ry) \\ 2(xy + rz) & 1 - 2(x² + z²) & 2(yz - rx) \\ 2(xz - ry) & 2(yz + rx) & 1 - 2(x²+y²) \end{bmatrix} $$

   The stretching matrix is diagonal and represented as a 3D vector $𝐒 = [x, \ y, \ z]$

   Covariance matrix (3x3) of 3D Gaussian cov3D: 𝚺 = 𝐑𝐒𝐒ᵀ𝐑ᵀ

3. Covariance matrix (3x3) is projected onto 2D screen cov: 𝚺’ = 𝐉 𝐖 𝚺 𝐖ᵀ𝐉ᵀ. Code

4. Take the inverse of 𝚺’ (𝚺’⁻¹), conic, to evaluate the 2D Gaussian PDF. Code

5. The extent of a point (Gaussian center) is a bounding square, where the “radius” from each side to the projected pixel is my_radius: 3σ. Code

   The radius of the circumscribed circle for a 2D Gaussian is the max eigenvalue of the 2D covariance matrix $𝐀 = [^{a \ b}_{b \ c}]$. The eigenvalues can be solved from:

   $$ det (𝐀 - λ⋅𝐈) = 0 \\ \begin{vmatrix} a-λ & b \\ b & c-λ\end{vmatrix} = 0 \\ (a-λ)(c-λ) - b^2 = 0 \\ λ^2 - (a+c)λ + ac-b^2 =0 $$

   Two roots: $λ₁,\ λ₂ = \frac{(a+c)}{2} ± \sqrt{\frac{(a+c)²}{4}-(ac-b²)}$

   1 2 3 4 5

   float det = (cov.x * cov.z - cov.y * cov.y); // determinant - - - float mid = 0.5f * (cov.x + cov.z); float lambda1 = mid + sqrt(max(0.1f, mid * mid - det)); float lambda2 = mid - sqrt(max(0.1f, mid * mid - det));

   Pixel coordinates: Scale the ND coordinates of x,y ∈ [-1,1] to image-grid coordiantes point_image [0,W] through viewport transformation: $x = \frac{W⋅(x-1)}{2} -0.5,\ y=\frac{H⋅(y-1)}{2} -0.5$

Prepare Tiles

(2024-02-02)

1. Obtain the total sum of touched tiles for all Gaussian centers by inclusive sum

   1 2 3 4 5 6

   cub::DeviceScan::InclusiveSum(geomState.scanning_space, geomState.scan_size, geomState.tiles_touched, geomState.point_offsets, P) - - - int num_rendered; // total number CHECK_CUDA(cudaMemcpy(&num_rendered, geomState.point_offsets + P - 1, sizeof(int), cudaMemcpyDeviceToHost), debug);

   • InclusiveSum produces a sequence of prefix sum for tiles_touched (the number of touched tiles) of 100k points.

     The pointer point_offsets points to the first byte of the 100k-byte sequence.

   • P = 100k bytes (char) is the number of points (Gaussian center).

     So, point_offsets + P - 1 is the last element in the prefix-sum sequence. Specifically, it’s the total number of touched tiles for all 100k points.

2. Evaluate each Gaussian to pair every touched tile’s index and Gaussian’s depth: Code

   1	duplicateWithKeys << <(P + 255) / 256, 256 >> > (

   Iterate each tile that a Gaussian overlaps, and combine the tile index and the Gaussian’s depth to form a key

   1 2 3 4 5

   for (int y = rect_min.y; y < rect_max.y; y++) { for (int x = rect_min.x; x < rect_max.x; x++) { gaussian_keys_unsorted[off] = key;

   • 100x100 image are divided to tiles with size of 16x16, so the thread gridDim: (7,7,1)

     For example, the above small Gaussian covers 9 tiles at: (0,1), (1,1), (2,1), (0,2), (1,2), (2,2), (0,3), (1,3), (2,3)

     The tile index is computed as y*grid.x + x. Therefore, the 9 tiles’ indices are: 8,9,10, 15,16,17, 22,23,24

   • Suppose the tile id is 24 and the Gaussian’s depth is 15.7 (cast to int 15), the corresponding pair’s key is:

     1 2 3

     tile id 24: 0000_0000_0000_0000_0000_0000_0001_1000 Shift left 32 bits: 0000_0000_0000_0000_0000_0000_0001_1000_0000_0000_0000_0000_0000_0000_0000_0000 combine depth (15): 0000_0000_0000_0000_0000_0000_0001_1000_0000_0000_0000_0000_0000_0000_0000_1111

   • Because each Gaussian is processed by a thread in parallel, the prefix sum point_offsets is referenced to locate the starting cell for each Gaussian to store keys into corresponding area of the array gaussian_keys_unsorted:

   • The value is the Gaussian’s index ranging in [0, 100k-1], i.e., the thread index idx:

     1 2 3

     auto idx = cg::this_grid().thread_rank(); --- gaussian_values_unsorted[off] = idx

3. With performing SortPairs, the tile-Gaussian pairs sequence (binningState.point_list_keys) is arranged based on the tile ID, and for keys with identical tile id, the depths are then sorted.

   1 2 3 4 5

   CHECK_CUDA(cub::DeviceRadixSort::SortPairs( ... binningState.point_list_keys_unsorted, binningState.point_list_keys, binningState.point_list_unsorted, binningState.point_list, ...

4. Evaluate each pair to identify the boundaries ranges of each tile for rendering. Code

   1	identifyTileRanges << <(num_rendered + 255) / 256, 256 >> > (

   • Count the number of tile-Gaussian pairs for each tile, as the threadIdx is the counter.

     1	auto idx = cg::this_grid().thread_rank();

   • Identify the tile’s boundary by detecting the change of tiles index in the list of the sorted tile-Gaussian keys:

     1	if (currtile != prevtile)

Render Pixel

(2024-02-05)

A block for a tile; A thread for a Gaussian; A pixel is an iterative composition of multiple Gaussian. Ultimately, in the end, a thread in a block corresponds to a pixel.

A thread syntheses a single pixel by performing alpha compositing Gaussian-by-Gaussian.

1
2

renderCUDA<NUM_CHANNELS> << <grid, block >> > (
// grid: (7,7,1), block: (16,16,1), 49*256 threads for 100x100 pix

• A pixel’s color is rendered within the tile encompassing it, based on the obtained sorted sequence of Gaussians’ indices.

• All pixels in a tile correspond to the same Gaussians, but with different weights, as the weights depend on distance from the pixel coordinates to the 2D Gaussian center: $exp(-½ (𝐱-\bm μ)^T \bm Σ_{(2D)}^{-1} (𝐱-\bm μ))$.

  1 2 3 4 5 6 7

  for (int j = 0; !done && j < min(BLOCK_SIZE, toDo); j++) { ... float2 xy = collected_xy[j]; // pixel coords float2 d = { xy.x - pixf.x, xy.y - pixf.y }; // dist float4 con_o = collected_conic_opacity[j]; // cov float power = -0.5f * (con_o.x * d.x * d.x + con_o.z * d.y * d.y) - con_o.y * d.x * d.y;

• The coordinates of the pixel to be rendered by a thread is obtained as follows:

  • pix_min = (2 * BLOCK_X, 1 * BLOCK_Y) = (32, 16)
  • pix_max = (max(32+BLOCK_X, W), max(16+BLOCK_Y, H)) = (48, 32)
  • pix = (32+block.thread_index().x, 16+block.thread_index().y)
  • pix_id = 100*pix.y + pix.x
  • tile id = 1*7 + 2 = 9
  • range = ranges[9], number of Gaussians for this tile.

• After the pixel is fully rendered as the accumulated transmittance T is close to 0.0, this thread is assigned to transfer data (Gaussian properties) from the global memory to shared memory.

(2023-02-06)

A 16×16 thread block works repeatedly for one tile.

In NeRF, a rendering batch comprises multiple rays emitted from pixels, while in 3DGS, a rendering batch is a tile (16x16) of pixels.

• Different tile has different number of tile-Gaussian pairs (range). Thus, each tile requires varying computations.

• Each pixel in a tile results from multiple (range) tile-Gaussian pairs. Each tile-Gaussian pair is a “filter composition” and requires a thread to execute once. As only a single 16x16 thread block is assigned to render the tile. To fulfill all the tile-Gaussian pairs composition, the equal amount (range) of thread executions are needed. Thus, the computation for a tile has to re-use the 16x16 thread block several times repeatedly, i.e., rounds times.

  1 2 3

  uint2 range = ranges[block.group_index().y * horizontal_blocks + block.group_index().x]; // given tile index, read (starting pair, ending tile-Gaussian pair) const int rounds = ((range.y - range.x + BLOCK_SIZE - 1) / BLOCK_SIZE); // the number of 16x16 blocks are allocated based on the number of tile-Gaussian pairs int toDo = range.y - range.x; // number of tile-Gaussian pairs to render the tile

  For example, if the tile 0 corresponds to 158 tile-Gaussian pairs in the sorted list: point_list_keys, the 16x16 thread block runs only once to render pixels in tile 0. And if tile 1’s range is 768 tile-Gaussian pairs, 3-round executions are needed.

• Every Gaussian gets added onto every pixel (color += color * alpha * T) until a pixel gets fully rendered, i.e., T is close to 0:

  1 2 3 4 5 6 7 8 9 10 11 12

  // Iterate tiles for (int i = 0; i < rounds; i++, toDo -= BLOCK_SIZE) { // if pixels in the tile are all rendered, break ... // Iterate Gaussians for (int j = 0; !done && j < min(BLOCK_SIZE, toDo); j++) { ... // Add a Gaussian to every pixel with specific weight for (int ch = 0; ch < CHANNELS; ch++) C[ch] += features[collected_id[j] * CHANNELS + ch] * alpha * T;

• The alpha compositing can be calculated in parallel, as the cumulative summation is definite and independent of the adding sequence.

(2024-04-27)

1. A tile (16x16 pixels) is rendered from many tile-Gaussian pairs, which are composited batch-by-batch iteratively.

2. Each iteration processes 16x16 (256) tile-Gaussian pairs, because each tile is allocated with 16x16 threads.

3. The shared memory is leverage to speed up the inner for loop, which is for compositing the contributing Gaussians for the pixel processed by the thread.

Render Depth

(2024-04-28)

Refer to code ashawkey/diff-gaussian-rasterization

The depth of a pixel is composited behind the alpha compositing of colors. Code.

1

D += depths[collected_id[j]] * alpha * T;

• depths is the z coordinate of 3D Gaussian centers in the camera space.
• collected_id is the Gaussians index stored in shared memory. j is the index of a Gaussian in a round.
• alpha is the portion of Gaussian’s color that will be used.
• T is the accumulated decay factor for the current Gaussian color passing through filter before it.

Similar to NeRF, where α is the probability of ray terminating and T is the prob of ray passing, the depth map is an expectation of Gaussians (“probability * depth”), where the weights (“probability”) are alpha * T.

(2024-05-05)

• Similar to MVSNet, by regarding the αT as the probability of depth, the “pre-defined hypothetical” depth values are aggregated by probabilities to form a predicted pixel depth.

• Ziyi Yang believes: Using z-coordinate in camera space to represent depth is acceptable, because the depth essentially represents relative spatial relations, similar to z coordinate.

  • However, robot0321 rebuttuled that regarding the z-value expectation as depth may cause error. And the depth map can be accquired by locating the frontmost point if there’s only one surface. conversation

Other papers also applied this form: FSGS, SparseGS

(2024-05-02)

• The depths of Gaussians in the camera space are already included in the geometryBuffer.

• The “buffer” memory allocated on GPU is for input data to kernel functions (depths, radii, points_xy_image, …) Code.

• The forward pass only performs depth rendering and return it, by mofifying files: cuda_rasterizer/forward.cu

  And change the function signatures in cuda_rasterizer/rasterizer_impl.cu.

Backward

Looking up definitions: backward.cu ⬅ rasterizer_impl.cu ⬅ rasterize_points.cu ⬅ __init__.py

bw render pixel color

(2024-02-09) Calling entry

The rendered pixel is derived from color (R,G,B) and opacity of each Gaussian.

Derivative flows backward:

The partial derivatives of Loss w.r.t. each Gaussian can be computed in parallel similar to forward rendering, as the contribution is a summation?

• Incoming upstream gradient: dL_dpixels
• Accumulated transmittance over all Gaussians is known, so accumulated transmittance of each Gaussian can be accquired with: $T_{curr} = \frac{T_{curr+1}}{(1-α_{curr})} $

(2024-02-10)

For pixel color scalar (R,G,B) in each channel k:

1. Partial derivative of pixel color w.r.t. each Gaussian’s color: α⋅T

   $$\rm \frac{∂C_{pixel}}{∂C_{k}} = α_{curr}⋅ T_{curr}$$

   dL_dcolors is the sum of 3 channels of all Gaussians that contribute to this pixel.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

   // Batchify Gaussians responsible for the pixel for (int i = 0; i < rounds; i++, toDo -= BLOCK_SIZE){ ... // Each round calculate a BLOCK_SIZE Gaussians for (int j = 0; !done && j < min(BLOCK_SIZE, toDo); j++){ ... T = T / (1.f - alpha); const float dchannel_dcolor = alpha * T; for (int ch = 0; ch < C; ch++){ // C=3 channels ... const float dL_dchannel = dL_dpixel[ch]; // add to previous dL_dcolors atomicAdd(&(dL_dcolors[global_id * C + ch]), dchannel_dcolor * dL_dchannel); } } }

2. Partial derivative of (pixel color) Loss w.r.t. each Gaussian’s alpha: dL_dalpha

   $$ \begin{aligned} \rm C_{pix} &= \rm C_{last-1} α_{last-1} T_{curr}(1-α_{curr})(1-α_{last}) + C_{last}α_{last}T_{curr}(1-α_{curr}) + C_{curr} α_{curr} T_{curr} + ⋯ \\ \rm \frac{∂C_{pix}}{∂α_{curr}} &= \rm - C_{last-1} α_{last-1} T_{curr}(1-α_{last}) - C_{last}α_{last}T_{curr} + C_{curr} T_{curr} \\ &= \rm (C_{curr} - \underbrace{C_{last-1} α_{last-1}}_{\text{accum rec}} (1-α_{last}) - C_{last}α_{last}) ⋅ T_{curr} \\ \rm \frac{∂L}{∂α_{curr}} &= \rm \frac{∂L}{∂C_{pix}}⋅ \frac{∂C_{pix}}{∂α_{curr}} \end{aligned} $$

   1 2 3 4 5 6 7 8 9 10 11

   for (int ch = 0; ch < C; ch++) // C=3 chnls { const float c = collected_colors[ch * BLOCK_SIZE + j]; accum_rec[ch] = last_alpha * last_color[ch] + (1.f - last_alpha) * accum_rec[ch]; last_color[ch] = c; const float dL_dchannel = dL_dpixel[ch]; dL_dalpha += (c - accum_rec[ch]) * dL_dchannel; ... } dL_dalpha *= T;

   Old notes

   $$ \rm \frac{∂C_{pixel}}{∂ α_{curr}} = C_{k} T_{curr} - \frac{∑_{m>curr}cₘ⋅αₘ⋅ Tₘ}{1-α_{curr}} $$

   A summation of subsequent Gaussians which are based on the current Gaussian.

   As the solving process starts from the rare Gaussian that depends on all previous Gaussians to, when calculating the current Gaussian, the summation of Gaussians affected by it is ready to use.

   ---

   Consider the contribution of background color to the pixel color finally: Code

   $$ \begin{aligned} \rm C_{pix} &= \rm C_{gs} + T_{final}C_{bg} \\ &= \rm α_{gs} c_{gs} + (1-α_{gs}) T_{final-1} C_{bg} \\ \\ \rm \frac{∂ L}{∂ α_{gs}} &= \rm \frac{∂ L}{∂ C_{pix}} ⋅ ( \frac{∂C_{pix}}{∂α_{gs}} + \frac{∂C_{pix}}{∂T_{final}} ⋅ \frac{∂T_{final}}{∂α_{gs}} ) \\ &= \rm \frac{∂L}{∂α_{gs}} + \frac{∂ L}{∂ C_{pix}} ⋅ C_{bg} ⋅ (-\frac{T_{final}}{(1-α_{gs})}) \end{aligned} $$

   1 2 3 4

   float bg_dot_dpixel = 0; for (int i = 0; i < C; i++) bg_dot_dpixel += bg_color[i] * dL_dpixel[i]; dL_dalpha += (-T_final / (1.f - alpha)) * bg_dot_dpixel;

3. Partial derivative of Loss w.r.t. 2D means:

   $$ \begin{aligned} G &= e^{-½ (\bm μ-𝐱)ᵀ \bm Σ⁻¹ (\bm μ-𝐱)} \\ &= exp(-½ ⋅ [μₓ-x \ μ_y-y] ⋅ [^{a \ b}_{d \ c}] ⋅ [^{μₓ-x} _{μ_y-y}])\\ &= exp(-½⋅ (a⋅Δₓ² + (b+d)⋅ΔₓΔ_y + c⋅Δ_y²)) \\ α &= o ⋅ G \\ \frac{∂α}{∂Δₓ} &= o⋅G⋅ (-aΔₓ - bΔ_y) \\ \frac{∂L}{∂μ_{x(flim)}} &= \frac{∂L}{∂α}⋅ \frac{∂α}{∂Δₓ}⋅ \frac{∂Δₓ}{∂μₓ} ⋅ \frac{∂μₓ}{∂μ_{x (film)}} \\ &= \frac{∂L}{∂α} ⋅o⋅G⋅ (-aΔₓ - bΔ_y) ⋅ 1 ⋅ \frac{W}{2} \end{aligned} $$

   • Although b=d, to be consistent with the derivative ∂L/∂b in the Jacobian matrix, the b and d keep separated instead of using b+d = 2b.

   1 2 3 4 5 6 7 8 9 10 11

   const float ddelx_dx = 0.5 * W; // viewport transform const float ddely_dy = 0.5 * H; const float dL_dG = con_o.w * dL_dalpha; const float gdx = G * d.x; const float gdy = G * d.y; const float dG_ddelx = -gdx * con_o.x - gdy * con_o.y; const float dG_ddely = -gdy * con_o.z - gdx * con_o.y; // Update gradients w.r.t. 2D mean position of the Gaussian atomicAdd(&dL_dmean2D[global_id].x, dL_dG * dG_ddelx * ddelx_dx); atomicAdd(&dL_dmean2D[global_id].y, dL_dG * dG_ddely * ddely_dy);

4. Partial derivative of Loss w.r.t. 3 elements a,b,c in the inverse of 2D covariance matrix, based on $α = o⋅G = o⋅exp(-\frac{1}{2}Δₓᵀ[^{a\ b}_{d\ c}]Δₓ)$:

   • Note: Here $[^{a\ b}_{d\ c}]$ represents the inverse cov 𝚺⁻¹, not the original cov2D 𝚺.

   $$ \frac{∂L}{∂a} = \frac{∂L}{∂α}⋅ \frac{∂α}{∂a} = \frac{∂L}{∂α}⋅ o ⋅ G ⋅ (-½Δₓ²) $$

   1 2 3

   atomicAdd(&dL_dconic2D[global_id].x, -0.5f * gdx * d.x * dL_dG); atomicAdd(&dL_dconic2D[global_id].y, -0.5f * gdx * d.y * dL_dG); atomicAdd(&dL_dconic2D[global_id].w, -0.5f * gdy * d.y * dL_dG);

5. Partial derivative of Loss w.r.t. opacity based on $α=oG$

   $$ \frac{∂L}{∂o} = \frac{∂L}{∂α} ⋅ \frac{∂α}{∂o} = \frac{∂L}{∂α}⋅ G $$

bw render pixel depth

(2024-05-04)

• Ziyi Yang has a PR only for depth forward and backward. 3DGS-PR#5

(2024-04-29)

The forward pass of ashawkey/diff-gaussian-rasterization also rendered alpha in addition to the depth map:

The weight of each Gaussian’s opacity is the exponential function, where the power depends on the distance from pixel (processed by the thread) to a Gaussian’s mean.

$$ \begin{aligned} α &= \text{opacity} ⋅ e^{-½\bm Δᵀ \bm Σ_{(2D)}^{-1} \bm Δ} \\ &= o ⋅ exp(-½ \begin{bmatrix} Δ_x & Δ_y \end{bmatrix} \begin{bmatrix} a & b \\ d & c \end{bmatrix} \begin{bmatrix} Δ_x \\ Δ_y \end{bmatrix} ) \\ &= o ⋅ exp(-0.5 ⋅(a ⋅ Δ_x^2 + c ⋅ Δ_y^2) - b ⋅ Δ_x Δ_y) \end{aligned} $$

Depth loss:

$$ \begin{aligned} L_d &= ½(d_{render} - d_{target})² \\ &= ½(∑_{n}dₙ αₙ Tₙ - d_{target})² \end{aligned} $$

• where n is the index of a Gaussian.

1. The partial derivative of pixel depth w.r.t. a Gaussian’s depth: Code

   $$ \frac{∂d_{render}}{∂dₙ} = αₙ Tₙ $$

   1	const float dpixel_depth_ddepth = alpha * T;

2. The partial derivative of Loss of depth w.r.t. a Gaussian’s alpha:

   Similar to rendering the color for a pixel:

   $$ \begin{aligned} L_d &= ½(∑_{n}dₙ αₙ Tₙ - d_{target})² \\ &= ½(d_{curr} α_{curr} T_{curr} + d_{last} ⋅α_{last}⋅ (1-α_{curr}) T_{curr} \\ &\quad + d_{last-1}⋅ α_{last-1}⋅ (1-α_{last})(1-α_{curr}) T_{curr} \\ &\quad + ⋯ - d_{target})² \end{aligned} $$

   The partial derivative of Loss of depth w.r.t. alpha of the current Gaussian:

   $$ \begin{aligned} \frac{∂L_d}{∂α_{curr}} &= d_{curr}⋅T_{curr} - d_{last} ⋅α_{last}⋅T_{curr} \\ &\quad - d_{last-1}⋅ α_{last-1}⋅ (1-α_{last})T_{curr} \\ &\quad - d_{last-2}⋅ α_{last-2} ⋅ (1-α_{last}) (1-α_{last-1})T_{curr} \\ &\quad + … \\ &= d_{curr}⋅T_{curr} - d_{last} ⋅α_{last}⋅\frac{T_{last}}{1-α_{curr}} \\ &\quad - d_{last-1}⋅ α_{last-1}⋅\frac{T_{last-1}}{1-α_{curr}} \\ &\quad - d_{last-2}⋅ α_{last-2} ⋅\frac{T_{last-2}}{1-α_{curr}} \\ &\quad + … \\ \end{aligned} $$

   Therefore, the general term for each Gaussian is:

   $$ \frac{∂L_d}{∂α_{curr}} = d_{curr}⋅T_{curr} - ∑_{m<curr} \frac{d_m α_m T_m}{1-α_{curr}} $$

   where the computation of the cumulative sum can be simplified using a recurrence relation (refer to will’s derivation):

   $$ \begin{aligned} & ∑_{m<curr} \frac{d_m α_m T_m}{1-α_{curr}} \\ &= ∑_{m<curr} \frac{d_m α_m T_m}{(1-α_{curr})T_{curr}}T_{curr} \\ &= ∑_{m<curr} \frac{d_m α_m T_m}{T_{last}}T_{curr} \\ &= \frac{d_{last} α_{last} \cancel{T_{last} }}{ \cancel{ T_{last} } }T_{curr} + ∑_{m<last} \frac{d_m α_m T_m}{T_{last}}T_{curr} \\ &= d_{last} α_{last}T_{curr} + (1-α_{last}) ∑_{m<last} \frac{d_m α_m T_m}{T_{last-1}}T_{curr} \\ \end{aligned} $$

   Therefore, the summation $∑_{m<curr}$ got split into 2 parts: the summation of terms before the previous 2 Gaussians (last-1), plus the previous one (last):

   The graph illustrates that the preceding result can be reused to compute the derivatives of the current Gaussian.

   The reuseable term, i.e., accum_depth_rec, is: $∑_{m<curr} \frac{d_m α_m T_m}{T_{last}}T_{curr}$

   1	accum_depth_rec = last_alpha * last_depth + (1.f - last_alpha) * accum_depth_rec;

   (2024-05-03)

   Since depth map (∑zαT) and RGB image (∑cαT) have similar generation process, just with different number of channels. the code of back-propagation for Gaussians’ depths can mimic the code of Gaussians’ colors. Code

3. The ashawkey’s code also renders each pixel’s alpha besides depth (∑αT) during forward, and produces a loss for pixel alpha $L_{alpha}$.

   Thus, the loss $L_{alpha}$ will affect the derivative of each pixel’s alpha dL_dalphas, and futhur each Gaussian’s alpha.

   To compute the derivative of the pixel alpha w.r.t. a Gaussian’s alpha, only Gaussians behind the current Gaussian will be considered.

   $$ \begin{aligned} α_{pixel} &= …+ α_{curr}T_{curr} + α_{last}(1-α_{curr})T_{curr} + α_{last-1}(1-α_{last})(1-α_{curr})T_{curr} + … \\ \frac{∂α_{pixel}}{∂α_{curr}} &= [1 - α_{last} -α_{last-1}(1-α_{last}) -α_{last-2}(1-α_{last-1})(1-α_{last})+…] T_{curr}\\ &= [1 - α_{last} - α_{last-1} \frac{T_{last-1}}{T_{last}} -α_{last-2}\frac{T_{last-2}}{T_{last}} + … ] T_{curr} \\ &= \cancel{[1 - α_{last} - ∑_{m<last}\frac{α_mT_m}{T_{last}}] T_{curr}} \quad \text{Can’t be recursive or explain the final $(1-α_{last})$}\\ &= [1 - ∑_{m<curr}\frac{α_mT_m}{T_{last}}] T_{curr} \\ &= [1 - α_{last} - (1-α_{last}) ∑_{m<last}\frac{α_mT_m}{T_{last-1}}] T_{curr} \end{aligned} $$

   • Multiplying by $(1-α_{last})$ is to use the sum of previously computed Gaussian

   (2024-05-04)

   • The recursive term should be a single term, instead of two-term combination. As shown above, if the sum $∑_{m<curr}$ doesn’t include $α_{last}$, the $∑_{m<last}$ indeed can be written as the previous result by multiplying with ($(1-α_{last})$), however when reversing back, the $- α_{last} - (1-α_{last}) ∑_{m<last}\frac{α_mT_m}{T_{last-1}}$ is not the $- ∑_{m<last}\frac{α_mT_m}{T_{last}}$, whereas it should equal to the 2-term sum: $- α_{last} - ∑_{m<last}\frac{α_mT_m}{T_{last}}$.

   1 2	accum_alpha_rec = last_alpha + (1.f - last_alpha) * accum_alpha_rec; dL_dopa += (1 - accum_alpha_rec) * dL_dalpha;

4. The partial derivative of depth loss w.r.t. each Gaussian’s opacity: Code

   Based on the relationship: $α=oG$

   $$ \frac{∂α}{∂o} = G, \quad \frac{∂L}{∂o} = \frac{∂L}{∂α} G $$

   1	atomicAdd(&(dL_dopacity[global_id]), G * dL_dopa);

   • I don’t know why he changed dL_dalpha to dL_dopa?

5. Subsequently, the partial derivative of alpha w.r.t. mean2D (or $\bm Δ$) and cov2D (a,b,c): Code

   Based on the formula: $α = o ⋅ exp(-0.5 ⋅(a ⋅ Δ_x^2 + c ⋅ Δ_y^2) - b ⋅ Δ_x Δ_y)$

   $$ \begin{aligned} \frac{∂α}{∂Δ_x} &= o ⋅ e^{-½\bm Δᵀ \bm Σ_{(2D)}^{-1} \bm Δ} ⋅ (-aΔ_x - bΔ_y) \\ \frac{∂α}{∂Δ_y} &= o ⋅ e^{-½\bm Δᵀ \bm Σ_{(2D)}^{-1} \bm Δ} ⋅ (-cΔ_y - bΔ_x) \\ \frac{∂α}{∂a} &= o ⋅ e^{-½\bm Δᵀ \bm Σ_{(2D)}^{-1} \bm Δ}⋅(-0.5Δ_x^2) \\ \frac{∂α}{∂b} &= o ⋅ e^{-½\bm Δᵀ \bm Σ_{(2D)}^{-1} \bm Δ}⋅(-Δ_x Δ_y) \\ \frac{∂α}{∂c} &= o ⋅ e^{-½\bm Δᵀ \bm Σ_{(2D)}^{-1} \bm Δ}⋅(-0.5Δ_y^2) \\ \end{aligned} $$

   snippet

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

   const float ddelx_dx = 0.5 * W; const float ddely_dy = 0.5 * H; const float dL_dG = con_o.w * dL_dopa; //I think it's dL_dalpha const float gdx = G * d.x; const float gdy = G * d.y; const float dG_ddelx = -gdx * con_o.x - gdy * con_o.y; const float dG_ddely = -gdy * con_o.z - gdx * con_o.y; // Update gradients w.r.t. 2D mean position of the Gaussian atomicAdd(&dL_dmean2D[global_id].x, dL_dG * dG_ddelx * ddelx_dx); atomicAdd(&dL_dmean2D[global_id].y, dL_dG * dG_ddely * ddely_dy); // Update gradients w.r.t. 2D covariance (2x2 matrix, symmetric) atomicAdd(&dL_dconic2D[global_id].x, -0.5f * gdx * d.x * dL_dG); atomicAdd(&dL_dconic2D[global_id].y, -0.5f * gdx * d.y * dL_dG); atomicAdd(&dL_dconic2D[global_id].w, -0.5f * gdy * d.y * dL_dG);

6. The partial derivative of mean2D to mean3D: Code

   (2024-05-04)

   Given transformation $mean3D_{cam} = W2C ⋅ mean3D_{world}$, only consider the z and the homogeneous coordinates.

   $$ \begin{bmatrix} \\ \\ mul3 \\ homo \end{bmatrix} = \begin{bmatrix} & & & \\ & & & \\ 2 & 6 & 10 & 14 \\ 3 & 7 & 11 & 15 \end{bmatrix} \begin{bmatrix} m.x \\ m.y \\ m.z \\ 1 \end{bmatrix} $$

   $$ \begin{aligned} depth_{cam} &= \frac{mul3}{homo} \\ \frac{∂depth_{cam}}{∂m.x} &= \frac{w2c[2] ⋅homo - mul3⋅ w2c[3]}{homo^2} \end{aligned} $$

   I don’t know why his code omitted the homo:

   1 2	float mul3 = view[2] * m.x + view[6] * m.y + view[10] * m.z + view[14]; dL_dmean2.x = (view[2] - view[3] * mul3) * dL_ddepth[idx];

bw cov2D

The cov2D $\bm Σ’_{ray}$ is originated from the 3D covariance matrix 𝚺 and the mean vector 𝐱 (ie, 𝛍) in world space. So the $\bm Σ’_{ray}$ is the starting point of the derivative of Loss w.r.t. the 𝚺 and 𝐱 of each Gaussian.

To align notations in previous posts, the covariance matrix in ray space is dentoed as 𝚺’, and the cov matrix in world space is 𝚺.

Note:

1. The clip coordinates aren’t used in the conversion for the 3D covariance matrix from world space to ray space. This is aligned with the EWA splatting. As the Gaussian center’s coordiantes are used in the Jacobian 𝐉, which is an approximation of perspective division, where the camera-space coordinates are supposed to be used, the 𝐭 in 𝐉 is coordinates of Gaussian center in camera space. So, only the viewmatrix “w2c” 𝐑 is applied to the world coordinates 𝐱.

2. However, the 2D Gaussian center on the screen indeed comes from clip coordinates, because points outside the frustrum don’t need to be rendered. Therefore, the projection matrix projmatrix is applied to the world coordinates 𝐱.

3. The above two branches both are derived from the world coordinates 𝐱, so the derivative of Loss w.r.t. 𝐱 ($\frac{∂L}{∂𝐱}$) comprises of two portions.

dΣ’⁻¹/dΣ'

(2024-02-11)

So far, the derivative of loss w.r.t. the inverse (conics, $(\bm Σ’)⁻¹$) of a 2D-plane covariance matrix $\bm Σ’$ (i.e., the 3D cov in ray space with 3rd row and column omitted) has been obtained. So, the derivative of loss w.r.t. the original 2D cov matrix 𝚺’ is $\frac{∂L}{∂\bm Σ’⁻¹}$ appended with the derivative of 𝚺’⁻¹ w.r.t. 𝚺'.

Consider 4 variables a, b, c, d form the matrix $\bm Σ’ = \begin{bmatrix}a & b \\ d & c \end{bmatrix}$, its inverse matrix is: $\bm Σ’⁻¹ = \frac{1}{ac-bd} \begin{bmatrix} c & -b \\ -d & a \end{bmatrix}$, where b=d.

The partial derivatives of the inverse matrix w.r.t. each variable: a,b,c,d are:

$$ \begin{aligned} \frac{∂ \bm Σ’⁻¹}{∂a} &= \frac{-c² + bc + dc - bd}{(ac-bd)²}, & \frac{∂ \bm Σ’⁻¹}{∂b} &= \frac{cd-ac-d²+ad}{(ac-bd)²} \\ \frac{∂ \bm Σ’⁻¹}{∂c} &= \frac{-bd+ba+da-a²}{(ac-bd)²}, & \frac{∂ \bm Σ’⁻¹}{∂d} &= \frac{cb-b²-ac+ab}{(ac-bd)²} \\ \end{aligned} $$

1
2
3
4
5
6
7

float denom = a * c - b * b;  // detminant
float dL_da = 0, dL_db = 0, dL_dc = 0;
float denom2inv = 1.0f / ((denom * denom) + 0.0000001f);
...
dL_da = denom2inv * (-c * c * dL_dconic.x + 2 * b * c * dL_dconic.y + (denom - a * c) * dL_dconic.z);
dL_dc = denom2inv * (-a * a * dL_dconic.z + 2 * a * b * dL_dconic.y + (denom - a * c) * dL_dconic.x);
dL_db = denom2inv * 2 * (b * c * dL_dconic.x - (denom + 2 * b * b) * dL_dconic.y + a * b * dL_dconic.z);

dΣ’/dΣ

(2024-02-12)

Derivative of 3D covariance matrix from ray space to camera space:

As the above 2D covariance matrix on plane is the 3D cov matrix 𝚺’ in the ray space with the 3rd row and column omitted. Thus, the next step to be calculated is the conversion from 𝚺’ in the 3D ray space to 𝚺 in the world space.

The 3D covariance matrix 𝚺’ in the ray space is obtained after performing viewing transform and projective transform:

$$ \begin{aligned} \bm Σ’_{ray} &= 𝐉⋅ 𝐑_{w2c} ⋅\bm Σ_{world}⋅ 𝐑ᵀ_{w2c} ⋅𝐉ᵀ \\ \begin{bmatrix} a & b & ∘ \\ b & c & ∘ \\ ∘ & ∘ & ∘ \end{bmatrix} &= \underbrace{ \begin{bmatrix} \frac{f_x}{t_z} & 0 & -\frac{f_x t_x}{t_z^2} \\ 0 & \frac{f_y}{t_z} & -\frac{f_y t_y}{t_z^2} \\ \frac{t_x}{‖𝐭‖} & \frac{t_y}{‖𝐭‖} & \frac{t_z}{‖𝐭‖} \end{bmatrix} \begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{bmatrix} }_{T} \begin{bmatrix} v_0 & v_1 & v_2 \\ v_1 & v_3 & v_4 \\ v_2 & v_4 & v_5 \\ \end{bmatrix} \underbrace{ \begin{bmatrix} R_{11} & R_{21} & R_{31} \\ R_{12} & R_{22} & R_{32} \\ R_{13} & R_{23} & R_{33} \end{bmatrix} \begin{bmatrix} \frac{f_x}{t_z} & 0 & \frac{t_x}{‖𝐭‖} \\ 0 & \frac{f_y}{t_z} & \frac{t_y}{‖𝐭‖} \\ -\frac{f_x t_x}{t_z^2} & -\frac{f_y t_y}{t_z^2} & \frac{t_z}{‖𝐭‖} \end{bmatrix} }_{Tᵀ} \\ &= \begin{bmatrix} T_{00} & T_{01} & T_{02} \\ T_{10} & T_{11} & T_{12} \\ T_{20} & T_{21} & T_{22} \\ \end{bmatrix} \begin{bmatrix} v_0 & v_1 & v_2 \\ v_1 & v_3 & v_4 \\ v_2 & v_4 & v_5 \\ \end{bmatrix} \begin{bmatrix} T_{00} & T_{10} & T_{20} \\ T_{01} & T_{11} & T_{21} \\ T_{02} & T_{12} & T_{22} \\ \end{bmatrix} \end{aligned} $$

The derivatives of 𝚺’ w.r.t. each element in the cov matrix $\bm Σ_{world}$ in world are:

$$ \begin{aligned} \frac{∂\bm Σ’_{ray}}{∂v_0} = \begin{bmatrix} T_{00}T_{00} & T_{00}T_{10} \\ T_{10}T_{00} & T_{10}T_{10} \end{bmatrix} \frac{∂\bm Σ’_{ray}}{∂v_1} = \begin{bmatrix} T_{00}T_{01} & T_{00}T_{11} \\ T_{10}T_{01} & T_{10}T_{11} \end{bmatrix} \frac{∂\bm Σ’_{ray}}{∂v_2} = \begin{bmatrix} T_{00}T_{02} & T_{00}T_{12} \\ T_{10}T_{02} & T_{10}T_{12} \end{bmatrix} \\ \frac{∂\bm Σ’_{ray}}{∂v_3} = \begin{bmatrix} T_{01}T_{01} & T_{01}T_{11} \\ T_{11}T_{01} & T_{11}T_{11} \end{bmatrix} \frac{∂\bm Σ’_{ray}}{∂v_4} = \begin{bmatrix} T_{01}T_{02} & T_{01}T_{12} \\ T_{11}T_{02} & T_{11}T_{12} \end{bmatrix} \\ \frac{∂\bm Σ’_{ray}}{∂v_5} = \begin{bmatrix} T_{02}T_{02} & T_{02}T_{12} \\ T_{12}T_{02} & T_{12}T_{12} \end{bmatrix} \end{aligned} $$

• Trick: Just find out the terms involving $v_0, v_1, v_2, v_3, v_4, v_5$

  For example, in the first matmul, the coefficients applied on v₀ are $T_{00},\ T_{10},\ T_{20}$ (a row). Then, in the outer matmul, the coefficients that multiplis with $v_0$ are $T_{00},\ T_{10},\ T_{20}$ (a column).

  So, the row and the column form a matrix:

  $$ \begin{bmatrix} T_{00} \\ T_{10} \\ T_{20} \end{bmatrix} \begin{bmatrix} T_{00} & T_{10} & T_{20} \end{bmatrix} → \begin{bmatrix} T_{00}T_{00} & T_{00}T_{10} & T_{00}T_{20} \\ T_{10}T_{00} & T_{10}T_{10} & T_{10}T_{20} \\ T_{20}T_{00} & T_{20}T_{10} & T_{20}T_{20} \end{bmatrix} $$

  The 3-rd row and column are omitted to yield the 2D covariance matrix on plane.

  Since the upstream derivative of loss w.r.t. $\bm Σ’_{ray}$ is a matrix as well, they need to do element-wise multiplication:

  $$ \begin{aligned} \frac{∂L}{∂v_0} &= \begin{bmatrix} \frac{∂L}{∂a} & \frac{∂L}{∂b} \\ \frac{∂L}{∂b} & \frac{∂L}{∂c} \end{bmatrix} ⊙ \begin{bmatrix} T_{00}T_{00} & T_{00}T_{10} \\ T_{10}T_{00} & T_{10}T_{10} \end{bmatrix} \\ &= \begin{bmatrix} \frac{∂L}{∂a} T_{00}T_{00} & \frac{∂L}{∂b} T_{00}T_{10} \\ \frac{∂L}{∂b} T_{10}T_{00} & \frac{∂L}{∂c} T_{10}T_{10} \end{bmatrix} \end{aligned} $$

  As loss is a scalar, the derivative of the loss w.r.t. $v_0$ should be the summation of all elements in the matrix (Need reference❗):

  $$ \frac{∂L}{∂v_0} = \frac{∂L}{∂a} T_{00}T_{00} + 2× \frac{∂L}{∂b}T_{00}T_{10} + \frac{∂L}{∂c} T_{10}T_{10} $$

• Details for v₄

  Similarly, the coefficients related to $v_4$ are the 3rd row of the right matrix 𝐓ᵀ, and the 2nd column of the left matrix 𝐓.

  $$ \begin{bmatrix} T_{01} \\ T_{11} \\ T_{21} \end{bmatrix} \begin{bmatrix} T_{02} & T_{12} & T_{22} \end{bmatrix} → \begin{bmatrix} T_{01}T_{02} & T_{01}T_{12} & T_{01}T_{22} \\ T_{11}T_{02} & T_{11}T_{12} & T_{11}T_{22} \\ T_{21}T_{02} & T_{21}T_{12} & T_{21}T_{22} \\ \end{bmatrix} $$

  The derivative of loss w.r.t. $v_1$

  $$ \begin{aligned} \frac{∂L}{∂v_1} &= \begin{bmatrix} \frac{∂L}{∂a} & \frac{∂L}{∂b} \\ \frac{∂L}{∂b} & \frac{∂L}{∂c} \end{bmatrix} ⊙ \begin{bmatrix} T_{01}T_{02} & T_{01}T_{12} \\ T_{11}T_{02} & T_{11}T_{12} \end{bmatrix} \\ &= T_{01}T_{02} \frac{∂L}{∂a} + (T_{01}T_{12} + T_{11}T_{02})\frac{∂L}{∂b} + T_{11}T_{12}\frac{∂L}{∂c} \end{aligned} $$

  Because the covariance matrix is symmatric (cov[1][2]=cov[2][1]), the effect attributed to the change of $v_1$ should double.

  $$ \frac{∂L}{∂v_4} = 2×T_{01}T_{02} \frac{∂L}{∂a} + 2×(T_{01}T_{12} + T_{11}T_{02})\frac{∂L}{∂b} + 2×T_{11}T_{12}\frac{∂L}{∂c} $$

• In the 3DGS code, dL_db had doubled.

  1 2 3 4 5 6 7 8

  glm::mat3 T = W * J; ... dL_dcov[6 * idx + 0] = (T[0][0] * T[0][0] * dL_da + T[0][0] * T[1][0] * dL_db + T[1][0] * T[1][0] * dL_dc); dL_dcov[6 * idx + 3] = (T[0][1] * T[0][1] * dL_da + T[0][1] * T[1][1] * dL_db + T[1][1] * T[1][1] * dL_dc); dL_dcov[6 * idx + 5] = (T[0][2] * T[0][2] * dL_da + T[0][2] * T[1][2] * dL_db + T[1][2] * T[1][2] * dL_dc); dL_dcov[6 * idx + 1] = 2 * T[0][0] * T[0][1] * dL_da + (T[0][0] * T[1][1] + T[0][1] * T[1][0]) * dL_db + 2 * T[1][0] * T[1][1] * dL_dc; dL_dcov[6 * idx + 2] = 2 * T[0][0] * T[0][2] * dL_da + (T[0][0] * T[1][2] + T[0][2] * T[1][0]) * dL_db + 2 * T[1][0] * T[1][2] * dL_dc; dL_dcov[6 * idx + 4] = 2 * T[0][2] * T[0][1] * dL_da + (T[0][1] * T[1][2] + T[0][2] * T[1][1]) * dL_db + 2 * T[1][1] * T[1][2] * dL_dc;

dΣ’/dT

(2024-02-13)

To solve the derivative of Loss w.r.t. $𝐭$ (in camera space), the chain is:

$$\frac{∂L}{∂t} = \frac{∂L}{\bm Σ’_{ray}} \frac{∂\bm Σ’_{ray}}{∂T} \frac{∂T}{∂J} \frac{∂J}{∂t}$$

The derivative of Loss w.r.t. 2D $\bm Σ’_{ray}$ has been obtained earlier. The next step is to calculate $\frac{∂\bm Σ’_{ray}}{∂T}$, where all variables except for T are treated as constants.

Based on the relationship:

$$ \bm Σ’_{ray} = 𝐓⋅\bm Σ_{world}⋅𝐓ᵀ \\ = \begin{bmatrix} T_{00} & T_{01} & T_{02} \\ T_{10} & T_{11} & T_{12} \\ T_{20} & T_{21} & T_{22} \end{bmatrix} \begin{bmatrix} v_{00} & v_{01} & v_{02} \\ v_{10} & v_{11} & v_{12} \\ v_{20} & v_{21} & v_{22} \end{bmatrix} \begin{bmatrix} T_{00} & T_{10} & T_{20} \\ T_{01} & T_{11} & T_{21} \\ T_{02} & T_{12} & T_{22} \end{bmatrix} $$

Represent the matrix $\bm Σ’_{ray}$ as a single generic term with varying indices: (inspired by David Levin surfaced by perplexity)

• an element in the result of $\bm Σ_{world}⋅𝐓ᵀ$ is $q$;
• an element in the $\bm Σ’_{ray}$ is $p$

$$ \begin{aligned} q_{ij} &= ∑ₖ₌₀² v_{ik} T_{jk} \\ p_{mn} &= ∑ₛ₌₀² T_{ms} q_{sn} = ∑ₛ₌₀² T_{ms} ∑ₖ₌₀² v_{sk} T_{nk}\\ \bm Σ’_{ray} &= \begin{bmatrix} p_{00} & p_{01} & p_{02} \\ p_{10} & p_{11} & p_{12} \\ p_{20} & p_{21} & p_{22} \end{bmatrix} \end{aligned} $$

Expand each $p_{mn}$:

$$ \begin{array}{ccc} \begin{aligned} p_{00} =& T_{00}(v_{00}T_{00} + v_{01}T_{01} + v_{02}T_{02}) \\ +& T_{01}(v_{10}T_{00} + v_{11}T_{01} + v_{12}T_{02}) \\ +& T_{02}(v_{20}T_{00} + v_{21}T_{01} + v_{22}T_{02}) \\ \end{aligned} & \begin{aligned} p_{01} =& T_{00}(v_{00}T_{10} + v_{01}T_{11} + v_{02}T_{12}) \\ +& T_{01}(v_{10}T_{10} + v_{11}T_{11} + v_{12}T_{12}) \\ +& T_{02}(v_{20}T_{10} + v_{21}T_{11} + v_{22}T_{12}) \\ \end{aligned} & \begin{aligned} p_{02} =& T_{00}(v_{00}T_{20} + v_{01}T_{21} + v_{02}T_{22}) \\ +& T_{01}(v_{10}T_{20} + v_{11}T_{21} + v_{12}T_{22}) \\ +& T_{02}(v_{20}T_{20} + v_{21}T_{21} + v_{22}T_{22}) \\ \end{aligned} \\ \begin{aligned} p_{10} =& T_{10}(v_{00}T_{00} + v_{01}T_{01} + v_{02}T_{02}) \\ +& T_{11}(v_{10}T_{00} + v_{11}T_{01} + v_{12}T_{02}) \\ +& T_{12}(v_{20}T_{00} + v_{21}T_{01} + v_{22}T_{02}) \\ \end{aligned} & p_{11} & p_{12} \\ \begin{aligned} p_{20} =& T_{20}(v_{00}T_{00} + v_{01}T_{01} + v_{02}T_{02}) \\ +& T_{21}(v_{10}T_{00} + v_{11}T_{01} + v_{12}T_{02}) \\ +& T_{22}(v_{20}T_{00} + v_{21}T_{01} + v_{22}T_{02}) \\ \end{aligned} & p_{21} & p_{22} \end{array} $$

The 3-rd row and column are omitted to become the 2x2 $\bm Σ’_{ray}$. So, only 4 elements affect the derivative of the $\bm Σ’_{ray}$. For example, the derivative of $\bm Σ’_{ray}$ w.r.t. $T₀₀$ only related to components containing $T_{00}$.

Calculate the derivative of each element $p_{mn}$ in the $\bm Σ’_{ray}$ w.r.t. $T_{00}$. A matrix is assembled:

$$ \begin{bmatrix} \frac{∂p_{00}}{∂T_{00}} & \frac{∂p_{01}}{∂T_{00}} \\ \frac{∂p_{10}}{∂T_{00}} & \frac{∂p_{11}}{∂T_{00}} \end{bmatrix} = \begin{bmatrix} \substack{2T_{00}v_{00} + v_{01}T_{01} + v_{02}T_{02} \\ + T_{01}v_{10} + T_{02}v_{20} } & v_{00}T_{10} + v_{01}T_{11} + v_{02}T_{12} \\ T_{10}v_{00} + T_{11}v_{10} + T_{12}v_{20} & 0 \end{bmatrix} $$

Therefore, the derivative of the scalar Loss w.r.t. T₀₀, i.e., $\frac{∂L}{∂T₀₀}$, is also a matrix:

$$ \frac{∂L}{∂T_{00}} = \frac{∂L}{∂\bm Σ’_{ray}}⊙ \frac{∂\bm Σ’_{ray}}{∂T_{00}} = \begin{bmatrix} \frac{∂L}{∂a} (2(T_{00}v_{00}+T_{01}v_{01}+T_{02}v_{02})) & \frac{∂L}{∂b} (T_{10}v_{00}+T_{11}v_{01}+T_{12}v_{02} ) \\ \frac{∂L}{∂b} (T_{10}v_{00}+T_{11}v_{10}+T_{12}v_{20} ) & 0 \end{bmatrix} $$

As the loss $L$ is a scalar, the derivative of $L$ w.r.t. a certain variable (e.g., T₀₀) is the total quantity of changes in all elements of a matrix caused by that variable’s unit perturbation. Thus, $\frac{∂L}{∂T₀₀}$ is a sum of all elements in the final “derivative matrix” of Loss w.r.t. T₀₀:

$$ \frac{∂L}{∂T_{00}} = \frac{∂L}{∂a}(2(T_{00}v_{00}+T_{01}v_{01}+T_{02}v_{02}) ) + \frac{∂L}{∂b}(2(T_{10}v_{00}+T_{11}v_{01}+T_{12}v_{02} ) ) $$

The dL_db in 3DGS Code had doubled:

1
2

float dL_dT00 = 2 * (T[0][0] * Vrk[0][0] + T[0][1] * Vrk[0][1] + T[0][2] * Vrk[0][2]) * dL_da +
(T[1][0] * Vrk[0][0] + T[1][1] * Vrk[0][1] + T[1][2] * Vrk[0][2]) * dL_db;

Similarly, the derivatives of Loss w.r.t. T₀₁, T₀₂, T₁₀, T₁₁, T₁₂ can be obtained. As T₂₀, T₂₁, T₂₂ are not involved in the 2D $\bm Σ’_{ray}$, they don’t contribute the derivative of $\bm Σ’_{ray}$.

$$ \frac{∂L}{∂𝐓} = \begin{bmatrix} \frac{∂L}{∂T_{00}} & \frac{∂L}{∂T_{01}} & \frac{∂L}{∂T_{02}} \\ \frac{∂L}{∂T_{10}} & \frac{∂L}{∂T_{11}} & \frac{∂L}{∂T_{12}} \\ 0 & 0 & 0 \end{bmatrix} $$

dT/dJ

(2024-02-14)

Based on the relationship:

$$ 𝐓 = 𝐉𝐖 = \begin{bmatrix} J₀₀ & J₀₁ & J₀₂ \\ J₁₀ & J₁₁ & J₁₂ \\ J₂₀ & J₂₁ & J₂₂ \end{bmatrix} \begin{bmatrix} W₀₀ & W₀₁ & W₀₂ \\ W₁₀ & W₁₁ & W₁₂ \\ W₂₀ & W₂₁ & W₂₂ \end{bmatrix} $$

The derivative of 𝐓 w.r.t. $J₀₀$

$$ \frac{∂T}{∂J_{00}} = \begin{bmatrix} W₀₀ & W₀₁ & W₀₂ \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} $$

The “derivative matrix” of Loss w.r.t. $J₀₀$

$$ \frac{∂L}{∂T} ⊙ \frac{∂T}{∂J_{00}} = \begin{bmatrix} \frac{∂L}{∂T_{00}} & \frac{∂L}{∂T_{01}} & \frac{∂L}{∂T_{02}} \\ \frac{∂L}{∂T_{10}} & \frac{∂L}{∂T_{11}} & \frac{∂L}{∂T_{12}} \end{bmatrix} ⊙ \begin{bmatrix} W₀₀ & W₀₁ & W₀₂ \\ 0 & 0&0 \end{bmatrix} \\ = \begin{bmatrix} \frac{∂L}{∂T_{00}} W₀₀ & \frac{∂L}{∂T_{01}} W₀₁ & \frac{∂L}{∂T_{02}} W₀₂ \\ 0 & 0 & 0 \end{bmatrix} $$

The derivative of Loss w.r.t. J₀₀ is the sum of all elements in the “derivative matrix”:

$$ \frac{∂L}{∂J₀₀} = \frac{∂L}{∂T_{00}} W₀₀ + \frac{∂L}{∂T_{01}} W₀₁ + \frac{∂L}{∂T_{02}} W₀₂ $$

In 3DGS code, the 3-rd row of the Jacobian matrix is set to 0 (as opacity isn’t obtained by integration along z-axis of ray space, but learned), thus no contribution to the derivative of Loss. Only compute the derivative of Loss w.r.t. J₀₀, J₀₂, J₁₁, J₁₂

$$ \frac{∂L}{∂𝐉} = \begin{bmatrix} \frac{∂L}{∂J₀₀} & 0 & \frac{∂L}{∂J₀₂} \\ 0 & \frac{∂L}{J₁₁} & \frac{∂L}{∂₁₂} \end{bmatrix} $$

1

float dL_dJ00 = W[0][0] * dL_dT00 + W[0][1] * dL_dT01 + W[0][2] * dL_dT02;

dJ/dt

The 3D mean 𝐭 in 𝐉 is the coordinates of a Gaussian center in camera space, Not the clip space, whereas the 2D mean 𝛍 indeed originates from the clip coordinates. Clip space is the scaled camera space for frustum clipping, and it’ll lead to 2D-plane projection coordinates (x,y) ranging in [-1,1]. However, the 𝐭 in 𝐉 must be camera-space coordinates, instead of the clip coordinates, because the perspective division approximated by the Jacobian 𝐉 uses coordinates of the 3D mean in camera space.

The 𝐉 is the projective transform that transforms a point to 3D ray space (screen is the ray space with z-axis omitted). 𝐉 is an approximation of the non-linear perspective division with the 1st-order Taylor expansion evaluated at the 3D Gaussian center 𝐭 in camera space.

In 3DGS, the 3rd row of 𝐉 is set to 0, as the opacity of each Gaussian is learned through gradient descent, instead of an integral over the viewing ray in the ray space. Thus, the z-axis of the ray space is useless in 3DGS.

Based on the relationship:

$$ 𝐉 = \begin{bmatrix} f_x/t_z & 0 & -f_x t_x / t_z² \\ 0 & f_y/t_z & -f_y t_y/t_z² \\ 0 & 0 & 0 \end{bmatrix} $$

The derivatives of 𝐉 w.r.t. $t_x,\ t_y,\ t_z$:

$$ \begin{aligned} \frac{∂𝐉}{∂t_x} &= \begin{bmatrix}0 & 0 & -f_x / t_z² \\ 0 & 0 & 0 \end{bmatrix} \\ \frac{∂𝐉}{∂t_y} &= \begin{bmatrix}0 & 0 & 0 \\ 0 & 0 & -f_y / t_z²\end{bmatrix} \\ \frac{∂𝐉}{∂t_z} &= \begin{bmatrix} -f_x⋅t_z^{-1} & 0 & 2f_x t_x ⋅t_z^{-3} \\ 0 & -f_y⋅t_z^{-1} & 2f_y t_y ⋅t_z^{-3} \\ \end{bmatrix} \end{aligned} $$

Combine upstream coefficients:

$$ \begin{aligned} \frac{∂L}{∂t_x} &= \frac{∂L}{∂𝐉}⊙ \frac{∂𝐉}{∂t_x} = \frac{∂L}{∂J_{02}} ⋅ -f_x/t_z^2 \\ \frac{∂L}{∂t_y} &= \frac{∂L}{∂𝐉}⊙ \frac{∂𝐉}{∂t_y} = \frac{∂L}{∂J_{12}} ⋅ -f_y/t_z^2 \\ \frac{∂L}{∂t_z} &= \frac{∂L}{∂𝐉}⊙ \frac{∂𝐉}{∂t_z} = \begin{bmatrix} \frac{∂L}{∂J₀₀} & 0 & \frac{∂L}{∂J₀₂} \\ 0 & \frac{∂L}{J₁₁} & \frac{∂L}{∂₁₂} \end{bmatrix} ⊙ \begin{bmatrix} -f_x⋅t_z^{-2} & 0 & 2f_x t_x ⋅t_z^{-3} \\ 0 & -f_y⋅t_z^{-2} & 2f_y t_y ⋅t_z^{-3} \\ \end{bmatrix} \\ &= \begin{bmatrix} \frac{∂L}{∂J₀₀} ⋅-f_x⋅t_z^{-2} & 0 & \frac{∂L}{∂J₀₂}⋅ 2f_x t_x ⋅t_z^{-3} \\ 0 & \frac{∂L}{J₁₁} ⋅-f_y⋅t_z^{-2} & \frac{∂L}{∂₁₂} ⋅2f_y t_y ⋅t_z^{-3} \end{bmatrix} \end{aligned} $$

Code

1
2
3
4

// h_x and h_y are f_x and f_y
float dL_dtx = x_grad_mul * -h_x * tz2 * dL_dJ02;
float dL_dty = y_grad_mul * -h_y * tz2 * dL_dJ12;
float dL_dtz = -h_x * tz2 * dL_dJ00 - h_y * tz2 * dL_dJ11 + (2 * h_x * t.x) * tz3 * dL_dJ02 + (2 * h_y * t.y) * tz3 * dL_dJ12;

dt/dx

After the projective transform, the derivative of $𝐭$ (Gaussian center coordinates) in camera space w.r.t. $𝐱$ in world space follows.

Based on the relationship of w2c viewmatrix:

$$ \begin{aligned} 𝐭_{cam} &= 𝐑_{w2c}⋅𝐱_{world} + 𝐓_{w2c} \\ &=\begin{bmatrix} R₀₀ & R₀₁ & R₀₂ \\ R₁₀ & R₁₁ & R₁₂ \\ R₂₀ & R₂₁ & R₂₂ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} + \begin{bmatrix} T_0 \\ T_1 \\ T_2 \end{bmatrix} \\ &=\begin{bmatrix} R₀₀x + R₀₁y + R₀₂z + T_0 \\ R₁₀x + R₁₁y + R₁₂z + T_1 \\ R₂₀x + R₂₁y + R₂₂z + T_2 \end{bmatrix} \end{aligned} $$

The derivative of $𝐭_{cam}$ w.r.t. $x, y, z$ of $𝐱_{world}$ are:

$$ \frac{∂𝐭}{∂x} = \begin{bmatrix} R₀₀\\ R₁₀\\ R₂₀ \end{bmatrix}, \frac{∂𝐭}{∂y} = \begin{bmatrix} R₀₁\\ R₁₁\\ R₂₁ \end{bmatrix}, \frac{∂𝐭}{∂z} = \begin{bmatrix} R₀₂\\ R₁₂\\ R₂₂ \end{bmatrix} $$

The derivative of $L$ w.r.t. $x, y, z$ of $𝐱_{world}$ are:

$$ \frac{∂L}{∂𝐭} \frac{∂𝐭}{∂x} = \frac{∂L}{∂t_x}\begin{bmatrix} R₀₀\\ R₁₀\\ R₂₀ \end{bmatrix}, \frac{∂L}{∂𝐭} \frac{∂𝐭}{∂y} = \frac{∂L}{∂t_y}\begin{bmatrix} R₀₁\\ R₁₁\\ R₂₁ \end{bmatrix}, \frac{∂L}{∂𝐭} \frac{∂𝐭}{∂z} = \frac{∂L}{∂t_z}\begin{bmatrix} R₀₂\\ R₁₂\\ R₂₂ \end{bmatrix} $$

As the x, y, z are individual variables to be optimized, the derivatives of L w.r.t. each of them shouldn’t add up.

1
2
3
4
5
6
7
8
9

__forceinline__ __device__ float3 transformPoint4x3(const float3& p, const float* matrix)
{
    float3 transformed = {
        matrix[0] * p.x + matrix[4] * p.y + matrix[8] * p.z + matrix[12],
        matrix[1] * p.x + matrix[5] * p.y + matrix[9] * p.z + matrix[13],
        matrix[2] * p.x + matrix[6] * p.y + matrix[10] * p.z + matrix[14],
    };
    return transformed;
}

bw preprocess

(2024-02-15)

The preprocess performed conversions from SH to RGB, from quaternion to a 3x3 rotation matrix, and from a stretching vector to the 3x3 covariance matrix in the world space.

Therefore, the inputs to the function BACKWARD::preprocessCUDA are the derivatives of Loss w.r.t. upstream variables: $\frac{∂L}{∂(RGB)},\ \frac{∂L}{∂\bm Σ_{world}},\ \frac{∂L}{∂𝐱_{world}},\ \frac{∂L}{∂\bm μ_{2D}}$. to solve the derivatives of Loss w.r.t. stretching vector, quaternion, and SH coeffs.

d_pix/d_world

(2024-02-16)

Gaussian center transformation from world space to 2D screen:

The derivative of Loss w.r.t. the 3D Gaussian mean 𝐱 in world space comprises of 2 streams:

$$\frac{∂L}{∂𝐱} = \frac{∂L}{∂𝐉} \frac{∂𝐉}{∂𝐱} + \frac{∂L}{∂\bm μ} \frac{∂\bm μ}{∂𝐱} $$

The first term resulted from 𝐉 has been obtained above, and the relationship between the 2D mean 𝛍 on screen and 3D 𝐱 is the full_proj_transform , i.e., projection matrix @ w2c

$$ \begin{aligned} \bm μᶜ &= 𝐏 [𝐑|𝐓] 𝐱 \\ \begin{bmatrix} μᶜ_x \\ μᶜ_y \\ μᶜ_z \\ μᶜ_w \end{bmatrix} &= \begin{bmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & \frac{f}{f-n} & \frac{-f n}{f-n} \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} R₀₀ & R₀₁ & R₀₂ & T₀ \\ R₁₀ & R₁₁ & R₁₂ & T₁ \\ R₂₀ & R₂₁ & R₂₂ & T₂ \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} \\ &= \begin{bmatrix} \frac{2n}{r-l} R₀₀ + \frac{r+l}{r-l} R₂₀ & \frac{2n}{r-l} R₀₁ + \frac{r+l}{r-l} R₂₁ & \frac{2n}{r-l} R₀₂ + \frac{r+l}{r-l} R₂₂ & \frac{2n}{r-l} T₀ + \frac{r+l}{r-l} T₂ & \\ \frac{2n}{t-b} R₁₀ + \frac{t+b}{t-b} R₂₀ & \frac{2n}{t-b} R₀₁ + \frac{t+b}{t-b} R₂₁ & \frac{2n}{t-b} R₀₂ + \frac{t+b}{t-b} R₂₂ & \frac{2n}{t-b} T₀ + \frac{t+b}{t-b} T₂ & \\ \frac{f}{f-n} R₂₀ & \frac{f}{f-n} R₂₁ & \frac{f}{f-n} R₂₂ & \frac{f}{f-n} T₂ + \frac{-f n}{f-n} \\ R₂₀ & R₂₁ & R₂₂ & T₂ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} \\ &= \begin{bmatrix} (\frac{2n}{r-l} R₀₀ + \frac{r+l}{r-l} R₂₀)x + (\frac{2n}{r-l} R₀₁ + \frac{r+l}{r-l} R₂₁)y + (\frac{2n}{r-l} R₀₂ + \frac{r+l}{r-l} R₂₂)z + (\frac{2n}{r-l} T₀ + \frac{r+l}{r-l} T₂ ) \\ (\frac{2n}{t-b} R₁₀ + \frac{t+b}{t-b} R₂₀)x + (\frac{2n}{t-b} R₀₁ + \frac{t+b}{t-b} R₂₁)y + (\frac{2n}{t-b} R₀₂ + \frac{t+b}{t-b} R₂₂)z + (\frac{2n}{t-b} T₀ + \frac{t+b}{t-b} T₂ ) \\ (\frac{f}{f-n} R₂₀)x + (\frac{f}{f-n} R₂₁)y + (\frac{f}{f-n} R₂₂)z + (\frac{f}{f-n} T₂ + \frac{-f n}{f-n}) \\ R₂₀x + R₂₁y + R₂₂z + T₂ \end{bmatrix} \end{aligned} $$

Perform perspective division to get the 2D-plane pixel coordinates:

$$ \begin{aligned} \bm μ &= \frac{1}{μᶜ_w} \bm μᶜ \\ \begin{bmatrix} μ_x \\ μ_y \\ μ_z \\ 1 \end{bmatrix} &= \begin{bmatrix} μᶜ_x/μᶜ_w \\ μᶜ_y/μᶜ_w \\ μᶜ_z/μᶜ_w \\ 1 \end{bmatrix} = \begin{bmatrix} μᶜ_x/(R₂₀x + R₂₁y + R₂₂z + T₂) \\ μᶜ_y/(R₂₀x + R₂₁y + R₂₂z + T₂) \\ μᶜ_z/(R₂₀x + R₂₁y + R₂₂z + T₂) \\ 1 \end{bmatrix} \end{aligned} $$

• where $(μ_x,\ μ_y)$ are the pixel coordinates, and $μ_z$ is similar to the z in ND space, but ranges in [0,1]. As $μ_z$ doesn’t involve into the image formation in 3DGS, it has no contribution to the Loss, and won’t participate the derivative of Loss w.r.t the world coordinates.

The derivative of $\bm μ$ w.r.t. $𝐱$:

$$ \begin{aligned} \frac{∂μ_x}{∂x} &= \frac{(\frac{2n}{r-l} R₀₀ + \frac{r+l}{r-l} R₂₀)(R₂₀x + R₂₁y + R₂₂z + T₂) - μᶜ_x R₂₀ }{(R₂₀x + R₂₁y + R₂₂z + T₂)^2} \\ &+ \frac{ (\frac{2n}{t-b} R₁₀ + \frac{t+b}{t-b} R₂₀) (R₂₀x + R₂₁y + R₂₂z + T₂) - μᶜ_y R₂₀ }{(R₂₀x + R₂₁y + R₂₂z + T₂)^2} \end{aligned} $$

The element indices in the float array proj is column-major: $\begin{bmatrix} 0 & 4 & 8 & 12 \\ 1 & 5 & 9 & 13 \\ 2 & 6 & 10 & 14 \\ 3 & 7 & 11 & 15 \end{bmatrix}$

1
2
3
4
5
6
7
8

float m_w = 1.0f / (m_hom.w + 0.0000001f);

glm::vec3 dL_dmean;
float mul1 = (proj[0] * m.x + proj[4] * m.y + proj[8] * m.z + proj[12]) * m_w * m_w;
float mul2 = (proj[1] * m.x + proj[5] * m.y + proj[9] * m.z + proj[13]) * m_w * m_w;
dL_dmean.x = (proj[0] * m_w - proj[3] * mul1) * dL_dmean2D[idx].x + (proj[1] * m_w - proj[3] * mul2) * dL_dmean2D[idx].y;
dL_dmean.y = (proj[4] * m_w - proj[7] * mul1) * dL_dmean2D[idx].x + (proj[5] * m_w - proj[7] * mul2) * dL_dmean2D[idx].y;
dL_dmean.z = (proj[8] * m_w - proj[11] * mul1) * dL_dmean2D[idx].x + (proj[9] * m_w - proj[11] * mul2) * dL_dmean2D[idx].y;

d_RGB/d_SH

d_cov3D/d_M

(2024-02-17)

Goal: Compute the derivative w.r.t. the entire matrix 𝐌 (not per element).

Given a quaternion: $q = [r,x,y,z]$, the rotation matrix is:

$$ 𝐑 = \begin{bmatrix} 1 - 2(y² + z²) & 2(xy - rz) & 2(xz + ry) \\ 2(xy + rz) & 1 - 2(x² + z²) & 2(yz - rx) \\ 2(xz - ry) & 2(yz + rx) & 1 - 2(x²+y²) \end{bmatrix} $$

Given a scaling vector $s=[s_x, s_y, s_z]$, the stretching matrix is:

$$ 𝐒 = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & s_z \end{bmatrix} $$

The covariance matrix can be decomposed by SVD as:

$$ \bm Σ = 𝐑𝐒𝐒ᵀ𝐑ᵀ $$

Use 𝐌 to represent 𝐑𝐒:

$$ 𝐌 = 𝐑𝐒 \\ = \begin{bmatrix} s_x(1 - 2(y² + z²)) & s_y(2(xy - rz)) & s_z(2(xz + ry)) \\ s_x(2(xy + rz)) & s_y(1 - 2(x² + z²)) & s_z(2(yz - rx)) \\ s_x(2(xz - ry)) & s_y(2(yz + rx)) & s_z(1 - 2(x²+y²)) s_x\end{bmatrix} $$

Therefore, $\bm Σ = 𝐌 𝐌ᵀ$

$$ \bm Σ = \begin{bmatrix} m₀₀ & m₀₁ & m₀₂ \\ m₁₀ & m₁₁ & m₁₂ \\ m₂₀ & m₂₁ & m₂₂ \\ \end{bmatrix} \begin{bmatrix} m₀₀ & m₁₀ & m₂₀ \\ m₀₁ & m₁₁ & m₂₁ \\ m₀₂ & m₁₂ & m₂₂ \\ \end{bmatrix} = \\ \begin{bmatrix} m₀₀²+m₀₁²+m₀₂² & m₀₀m₁₀+m₀₁m₁₁+m₀₂m₁₂ & m₀₀m₂₀+m₀₁m₂₁+m₀₂m₂₂ \\ m₁₀m₀₀+m₁₁m₀₁+m₁₂m₀₂ & m₁₀²+m₁₁²+m₁₂² & m₁₀m₂₀+m₁₁m₂₁+m₁₂m₂₂ \\ m₂₀m₀₀+m₂₁m₀₁+m₂₂m₀₂ & m₂₀m₁₀+m₂₁m₁₁+m₂₂m₁₂ & m₂₀²+m₂₁²+m₂₂² \\ \end{bmatrix} $$

The partial derivative of covariance matrix w.r.t. the element m₀₀:

$$ \frac{∂\bm Σ}{∂m₀₀} = \begin{bmatrix} 2m₀₀ & m₁₀ & m₂₀ \\ m₁₀ & 0 & 0 \\ m₂₀ & 0 & 0 \end{bmatrix} $$

The contribution of m₀₀ to the 𝚺 is the summation of all elements. Similarly, other elements’ contiribution to d𝚺 are as follows:

$$ \begin{aligned} \frac{∂\bm Σ}{∂m₀₀} = 2(m₀₀+m₁₀+m₂₀)\ & \frac{∂\bm Σ}{∂m₀₁} = 2(m₀₁+m₁₁+m₂₁) & \frac{∂\bm Σ}{∂m₀₂} = 2(m₀₂+m₁₂+m₂₂) \\ \frac{∂\bm Σ}{∂m₁₀} = 2(m₀₀+m₁₀+m₂₀)\ & \frac{∂\bm Σ}{∂m₁₁} = 2(m₀₁+m₁₁+m₂₁) & \frac{∂\bm Σ}{∂m₁₂} = 2(m₀₂+m₁₂+m₂₂) \\ \frac{∂\bm Σ}{∂m₂₀} = 2(m₀₀+m₁₀+m₂₀)\ & \frac{∂\bm Σ}{∂m₂₁} = 2(m₀₁+m₁₁+m₂₁) & \frac{∂\bm Σ}{∂m₂₂} = 2(m₀₂+m₁₂+m₂₂) \end{aligned} $$

$$ \frac{∂\bm Σ}{∂𝐌 } = 2 \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} m₀₀ & m₀₁ & m₀₂ \\ m₁₀ & m₁₁ & m₁₂ \\ m₂₀ & m₂₁ & m₂₂ \\ \end{bmatrix} $$

Concat with the upstream coefficient to get the derivative of Loss w.r.t. the matrix 𝐌: $\frac{∂L}{∂𝐌 } = \frac{∂L}{∂\bm Σ} \frac{∂\bm Σ}{∂𝐌 }$.

• In the code, however, $\frac{∂\bm Σ}{∂𝐌 }$ is on the left: $\frac{∂L}{∂𝐌 } = \frac{∂\bm Σ}{∂𝐌 } \frac{∂L}{∂\bm Σ}$

• Because the $\frac{∂L}{∂𝐌 }$ to be solved is a derivative w.r.t. the entire matrix 𝐌, not for each element, the 2 “derivative matrices” should perform matrix multiplication to get all terms mixtured completely, rather than an elementise product:

$$ \frac{∂L}{∂𝐌 } = \frac{∂\bm Σ}{∂𝐌 } \frac{∂L}{∂\bm Σ} \\ =\begin{bmatrix} 2(m₀₀+m₁₀+m₂₀) & ⋯ & ⋯\\ 2(m₀₀+m₁₀+m₂₀) & ⋯ & ⋯\\ ⋯ & ⋯ & ⋯ \end{bmatrix} \begin{bmatrix} \frac{∂L}{∂v_0} & \frac{∂L}{∂v_1} & \frac{∂L}{∂v_2} \\ \frac{∂L}{∂v_1} & \frac{∂L}{∂v_3} & \frac{∂L}{∂v_4} \\ \frac{∂L}{∂v_2} & \frac{∂L}{∂v_4} & \frac{∂L}{∂v_5} \end{bmatrix} $$

1

glm::mat3 dL_dM = 2.0f * M * dL_dSigma;

• glm performs matrix multiplication according to the same rules as in the math textbook, and the only difference is that the row and column indices for an elements are reversed: mat[col][row] for an element; mat[col] for a column vector.
  • Matrices and Quaternions FAQ - opengl-tutorial
  • Tutorial 3 : Matrices - opengl-tutorial

dM/ds

Goal: Compute derivative of loss w.r.t. each element in the scaling vector.

In the code, the 𝐌 =𝐒 𝐑, not 𝐑𝐒,

$$ 𝐌 =\begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & s_z \end{bmatrix} \begin{bmatrix} 1 - 2(y² + z²) & 2(xy - rz) & 2(xz + ry) \\ 2(xy + rz) & 1 - 2(x² + z²) & 2(yz - rx) \\ 2(xz - ry) & 2(yz + rx) & 1 - 2(x²+y²) \end{bmatrix} \\ =\begin{bmatrix} s_x(1 - 2(y² + z²)) & s_x(2(xy - rz)) & s_x(2(xz + ry)) \\ s_y(2(xy + rz)) & s_y(1 - 2(x² + z²)) & s_y(2(yz - rx)) \\ s_z(2(xz - ry)) & s_z(2(yz + rx)) & s_z(1 - 2(x²+y²)) \end{bmatrix} $$

Calculate the partial derivative of 𝐌 w.r.t. the scaling vector 𝐒 by element:

$$ \frac{∂𝐌 }{∂s_x} = \begin{bmatrix} 1-2(y² + z²) & 2(xy - rz) & 2(xz + ry) \\ 0 & 0 & 0 \\ 0 & 0 &0 \end{bmatrix} $$

As here it’s computing the derivative of the loss w.r.t. each element, the multiplication with the upstream derivative part is an element-wise product:

$$ \frac{∂L}{∂s_x} = \frac{∂L}{∂𝐌 }\frac{∂𝐌 }{∂s_x} = \\ \begin{bmatrix} s_x(1 - 2(y² + z²)) & s_x(2(xy - rz)) & s_x(2(xz + ry)) \\ ⋯ & ⋯ & ⋯ \\ ⋯ & ⋯ & ⋯ \\ \end{bmatrix} ⊙ \begin{bmatrix} 1-2(y² + z²) & 2(xy - rz) & 2(xz + ry) \\ 0 & 0 & 0 \\ 0 & 0 &0 \end{bmatrix} $$

Because glm indexes elements by columns, to easily access a row in the above 2 matrices, their transposed matrices are used:

1
2
3
4
5
6

glm::mat3 Rt = glm::transpose(R);
glm::mat3 dL_dMt = glm::transpose(dL_dM);

// Gradients of loss w.r.t. scale
glm::vec3* dL_dscale = dL_dscales + idx;
dL_dscale->x = glm::dot(Rt[0], dL_dMt[0]);	// scalar

• mat[0] takes out a column, as the indices in glm is column-major. 9. Matrix columns

dM/dq

Goal: Compute derivative of loss w.r.t. each element in the quaternion vector (r,x,y,z).

Based on the realtionship:

$$ 𝐌 =\begin{bmatrix} s_x(1 - 2(y² + z²)) & s_x(2(xy - rz)) & s_x(2(xz + ry)) \\ s_y(2(xy + rz)) & s_y(1 - 2(x² + z²)) & s_y(2(yz - rx)) \\ s_z(2(xz - ry)) & s_z(2(yz + rx)) & s_z(1 - 2(x²+y²)) \end{bmatrix} $$

$$ \frac{∂𝐌 }{∂r} = \begin{bmatrix} 0 & -2s_x z & 2s_x y \\ 2s_y z & 0 & -2s_y x \\ -2s_z y & 2s_z x & 0 \end{bmatrix} $$

Concat with the obtained upstream derivative of Loss w.r.t. 𝐌 through element-wise (Hadamard) product:

$$ \frac{∂L}{∂r} = \frac{∂L}{∂𝐌 } \frac{∂𝐌 }{∂r} = \\ \begin{bmatrix} \frac{∂L}{∂m_{00}} & \frac{∂L}{∂m_{01}} & \frac{∂L}{∂m_{02}} \\ \frac{∂L}{∂m_{10}} & \frac{∂L}{∂m_{11}} & \frac{∂L}{∂m_{12}} \\ \frac{∂L}{∂m_{20}} & \frac{∂L}{∂m_{21}} & \frac{∂L}{∂m_{22}} \\ \end{bmatrix} ⊙ \begin{bmatrix} 0 & -2s_x z & 2s_x y \\ 2s_y z & 0 & -2s_y x \\ -2s_z y & 2s_z x & 0 \end{bmatrix} \\ = \begin{bmatrix} 0 & \frac{∂L}{∂m_{01}} (-2s_x z) & \frac{∂L}{∂m_{02}} 2s_x y \\ \frac{∂L}{∂m_{10}} 2s_y z & 0 & \frac{∂L}{∂m_{12}} (-2s_y x) \\ \frac{∂L}{∂m_{20}} (-2s_z y) & \frac{∂L}{∂m_{21}} 2s_z x & 0 \\ \end{bmatrix} $$

$$ $$

Sum all element in the result matrix $\frac{∂L}{∂r}$:

1
2
3
4
5
6
7
8
9

dL_dMt[0] *= s.x;
dL_dMt[1] *= s.y;
dL_dMt[2] *= s.z;

// Gradients of loss w.r.t. normalized quaternion
glm::vec4 dL_dq;
dL_dq.x = 2 * z * (dL_dMt[0][1] - dL_dMt[1][0]) 
        + 2 * y * (dL_dMt[2][0] - dL_dMt[0][2]) 
        + 2 * x * (dL_dMt[1][2] - dL_dMt[2][1]);

Finally, calculate the derivative of loss for the normalization process of the quaternion.

Based on the normalization operation:

$$ 𝐪_{unit} = \frac{1}{‖𝐪‖} ⋅ 𝐪 = \frac{1}{\sqrt{r²+x²+y²+z²}} \begin{bmatrix} r \\ x \\ y \\ z \end{bmatrix} \\ \frac{∂𝐪}{∂r} = \frac{1}{r²+x²+y²+z²} - \frac{r²}{(r²+x²+y²+z²)^{3/2}} $$

It seems that the derivatives of the normalization step contributions are not considered in the code:

1
2
3
4

// Gradients of loss w.r.t. unnormalized quaternion
float4* dL_drot = (float4*)(dL_drots + idx);
*dL_drot = float4{ dL_dq.x, dL_dq.y, dL_dq.z, dL_dq.w };
//dnormvdv(float4{ rot.x, rot.y, rot.z, rot.w }, float4{ dL_dq.x, dL_dq.y, dL_dq.z, dL_dq.w });