旋转矩阵
-
乘以一个向量时,改变向量方向的矩阵
-
表示了不同维度坐标的线性变换
-
作用:把向量(默认绕原点、逆时针)的旋转用矩阵乘法表示
-
对于一个二维向量,旋转关系用矩阵乘法形式为:
$$ \begin{pmatrix} x’ \\ y' \end{pmatrix} = M_{2×2} \begin{pmatrix} x \\ y \end{pmatrix} $$
用待定系数法可以确定各元素
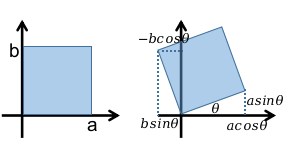
对于(a,0)点:
$$ \begin{pmatrix} acosθ \\ asinθ \end{pmatrix} = \begin{pmatrix} A & B \\ C & D \end{pmatrix}
\begin{pmatrix} a \\ 0 \end{pmatrix} $$
解得:$A=cosθ, C=sinθ$; 同理代入(0,b)点,可解得:$B=-sinθ, D=cosθ$,所以旋转矩阵为:
$$ \begin{pmatrix} cosθ & -sinθ \\ sinθ & cosθ \end{pmatrix} $$
旋转矩阵的逆
-
等于它的转置($R_θ^{-1}=R_θ^T$)
-
因为旋转矩阵是一个正交矩阵
-
逆操作就是顺时针旋转相同的角度,也就是正向旋转$-θ$,代入得:
$$ \begin{pmatrix} cosθ & sinθ \\ -sinθ & cosθ \end{pmatrix} $$
即为旋转矩阵的转置
齐次坐标
-
向量最后加个0,点最后加个1
-
3D vector: $(x,y,z,0)^T$
3D point: $(x,y,z,1)^T$ -
作用:平移变换也可写成一个矩阵
-
对于平移关系:
$$ \begin{cases} x’ = x + t_x \\ y’ = y + t_y \end{cases} $$
x,y方向都没有旋转,所以旋转矩阵为:
$$ \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} $$
写成齐次坐标:
$$ \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{pmatrix} $$
只有平移,附加到后面:
$$ \begin{pmatrix} x’ \\ y’ \\ 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 0 \end{pmatrix} $$
-
同一点的表示不唯一:
$$ \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} kx \\ ky \\ kz \\ k \end{pmatrix} $$
仿射变换
- 旋转变换和平移变换拼成一个矩阵